"RedBlackTree" (Data Structure)
"RedBlackTree" (Data Structure)
"RedBlackTree"
represents a mutable, self-balancing binary search tree, where the values stored at each node are general expressions.
Details


- A binary search tree stores data in a sorted form that allows quick insertion operations. A self-balancing binary search tree makes sure that the heights of all branches are balanced; this helps operations to be efficient despite arbitrary insertions and deletions.
-
CreateDataStructure[ "RedBlackTree"] create a new empty "RedBlackTree" CreateDataStructure["RedBlackTree",v{l,r}] create a new "RedBlackTree" with specified initial value v and specified left and right children CreateDataStructure["RedBlackTree",tree,p] create a new "RedBlackTree" with specified tree and ordering function p Typed[x,"RedBlackTree"] give x the type "RedBlackTree" - For a data structure of type "RedBlackTree", the following operations can be used:
-
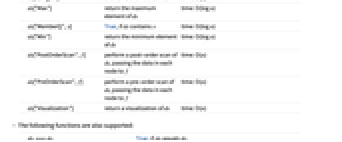
ds["BreadthFirstScan",f] perform a breadth-first scan of ds, passing the data in each node to f time: O(n) ds["Copy"] return a copy of ds time: O(n) ds["Delete",x] delete x from ds time: O(log n) ds["DeleteAll"] delete all elements from ds time: O(n) ds["DropMax"] remove the maximum element of ds and return it time: O(log n) ds["DropMin"] remove the minimum element of ds and return it time: O(log n) ds["Elements"] return a list of the elements of ds time: O(n) ds["EmptyQ"] True, if ds has no nodes time: O(1) ds["FreeQ",x] True, if ds does not contain x time: O(log n) ds["InOrderScan",f] perform an in-order scan of ds, passing the data in each node to f time: O(n) ds["Insert",x] insert x into ds time: O(log n) ds["Length"] the number of nodes in ds time: O(1) ds["Max"] return the maximum element of ds time: O(log n) ds["MemberQ",x] True, if ds contains x time: O(log n) ds["Min"] return the minimum element of ds time: O(log n) ds["PostOrderScan",f] perform a post-order scan of ds, passing the data in each node to f time: O(n) ds["PreOrderScan",f] perform a pre-order scan of ds, passing the data in each node to f time: O(n) ds["Visualization"] return a visualization of ds time: O(n) - The following functions are also supported:
-
dsi===dsj True, if dsi equals dsj FullForm[ds] the full form of ds Information[ds] information about ds InputForm[ds] the input form of ds Normal[ds] convert ds to a normal expression - The order of two elements is determined by the order function p, following the interpretation given by the order function of Sort. The default order function is Order.
- The "RedBlackTree" maintains a balanced property that the height of each subtree never differs by more than 1.
- If the initial tree specification is Null, an empty "RedBlackTree" is created.
Examples
open all close allBasic Examples (1)
A new "RedBlackTree" can be created with CreateDataStructure:
Scope (4)
Information (1)
A new "RedBlackTree" can be created with CreateDataStructure:
Balancing (1)
Ordering (1)
See Also
TreeGraph Graph Order CreateDataStructure DataStructure
Data Structures: AVLTree BinaryTree SortedKeyStore
Related Guides
History
Introduced in 2024 (14.0)