WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

"SortedMultiset" (Data Structure)

"SortedMultiset"

represents a multiset where the members are general expressions and are kept in a sorted order.

Details

  • A sorted multiset is useful for efficient insertion and removal as well as membership testing where the same element can appear more than once:
  • CreateDataStructure["SortedMultiset"]create a new empty "SortedMultiset" that uses canonical ordering
    CreateDataStructure["SortedMultiset",elems]create a new "SortedMultiset" with elements elems
    CreateDataStructure["SortedMultiset",elems,p]create a new "SortedMultiset" with specified elements and ordering function p
    Typed[x,"SortedMultiset"]give x the type "SortedMultiset"
  • For a data structure of type "SortedMultiset", the following operations can be used:
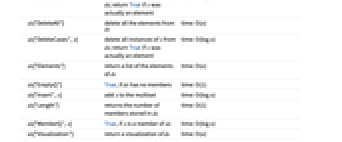
  • ds["Cases",elem]returns members of the multiset that match elemtime: O(log n)
    ds["Count", elem]returns the number of elements that match elemtime: O(log n)
    ds["Delete",x]delete one instance of x from ds; return True if x was actually an elementtime: O(log n)
    ds["DeleteAll"]delete all the elements from dstime: O(n)
    ds["DeleteCases",x]delete all instances of x from ds; return True if x was actually an elementtime: O(log n)
    ds["Elements"]return a list of the elements of dstime: O(n)
    ds["EmptyQ"]True, if ds has no memberstime: O(1)
    ds["Insert",x]add x to the multisettime: O(log n)
    ds["Length"]returns the number of members stored in dstime: O(1)
    ds["MemberQ",x]True, if x is a member of dstime: O(log n)
    ds["Visualization"]return a visualization of dstime: O(n)
  • The following functions are also supported:
  • dsi===dsjTrue, if dsi equals dsj
    FullForm[ds]full form of ds
    Information[ds]information about ds
    InputForm[ds]input form of ds
    Normal[ds]convert ds to a normal expression

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

A new "HashSet" can be created with CreateDataStructure:

In[1]:=1
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-ck3oom
Out[1]=1

Insert into the set:

In[2]:=2
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-84r1md

There is one element in the set:

In[3]:=3
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-tnm4iz
Out[3]=3

Test if an expression is stored:

In[4]:=4
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-kfcutb
Out[4]=4

If an expression is not stored, False is returned:

In[5]:=5
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-2ymbbr
Out[5]=5

Remove an element from the set. If something was actually removed, return True:

In[6]:=6
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-3dkxgf

Now there are two elements in the set:

In[7]:=7
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-l1py1j
Out[7]=7

Return an expression version of ds:

In[8]:=8
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-dbekgb
Out[8]=8

Insert a number of elements:

In[1]:=1
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-mfljzp

A visualization of the data structure can be generated:

In[2]:=2
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-uvwa1b
Out[2]=2

This shows how the data is sorted and contains multiple elements.

An ordering function can be given for a sorted multiset:

In[1]:=1
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-tm669

Insert two elements:

In[2]:=2
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-46x6du

These elements are all equal according to the ordering function:

In[3]:=3
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-yo6xa5
Out[3]=3

Remove an element:

In[4]:=4
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-vheel1
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-n32j59
Out[5]=5

Scope  (1)Survey of the scope of standard use cases

Information  (1)

A new "SortedMultiset" can be created with CreateDataStructure:

In[1]:=1
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-wn7q0m
Out[1]=1

Information about the data structure ds:

In[2]:=2
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-5du3om
Out[2]=2

Possible Issues  (1)Common pitfalls and unexpected behavior

Set Membership  (1)

If an ordering function is given, this is used to specify set membership:

In[1]:=1
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-kcurc1

This returns True because the ordering function only looks at the first element:

In[2]:=2
✖
https://wolfram.com/xid/0o85higkmkcvnt89474kc3fc8o76-b6b4af
Out[2]=2