ウェーブレットを定義する

正しいテンプレートを使うことで，ウェーブレット解析フレームワークに組み込めるウェーブレットを定義することができる．ウェーブレット wave は wfam[args]という形式であり，ここで wfam はウェーブレット族を示すシンボルを意味し，args は必要な指定を提供する．
wfam がシステムによりウェーブレット族と認識されるようにするためには，特性 wfam[patt]["WaveletQ"]がTrueに設定されている必要がある．ここで patt は受け入れられる引数 args にマッチするパターンである．
WaveletQ
シンボルがユーザのウェーブレットならばTrueに設定する
ウェーブレットの初期化特性
ユーザのウェーブレットは直交も双直交もサポートされている．直交ウェーブレットは特性 wfam[args]["OrthogonalQ"]を，双直交ウェーブレットは特性 wfam[args]["BiorthogonalQ"]を設定して示される．
"OrthogonalQ"
ウェーブレットが直交ならばTrueに設定する
"BiorthogonalQ"
ウェーブレットが双直交ならばTrueに設定する
ウェーブレットの特性
主なローパスフィルタ係数を計算するためには，特性 wfam[args]["PrimalLowpass",prec]を設定しなければならない．ここで prec はフィルタ係数の精度を示す．同様に，デュアルローパスフィルタ係数を計算するためには"DualLowpass"を設定しなければならない．"PrimalLowpass"と"DualLowpass"のどちらの特性も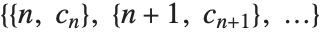という形式のリストを返すことが想定されている．ここで 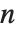は指標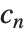， は対応するフィルタ係数である．形式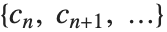のリストが返されたら，指標 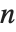は0から始まると想定される．フィルタ係数 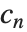が数値ではなく，指標 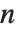が整数でない場合は，エラーメッセージが出る．
例題

フランクリン(Franklin)ウェーブレット

フランクリンウェーブレット族を定義する．
ウェーブレットを初期化する：
特性を設定する：
フランクリンウェーブレット係数は，積分により与えられる：
これでユーザのウェーブレットに関する上記の定義が，さまざまなウェーブレット操作を実行するために使えるようになった．
フィルタ係数を計算する：
スケーリング関数は，再帰方程式 を使って計算される．ここで はローパスフィルタ係数である．
スケーリング関数を計算する：
ウェーブレット変換を実行する：

ルジャンドル(Legendre)のウェーブレット

次はルジャンドルのウェーブレットの例である．
ウェーブレットを初期化する：
ルジャンドルのウェーブレットは直交ではないが，ウェーブレット変換を実行するためには，それをTrueに設定する必要がある：
ローパスフィルタ係数を計算する関数を指定する：
フィルタ係数を計算する：
スケーリング関数を計算する：
ウェーブレット関数は再帰方程式 を使って計算される．ここで はハイパスフィルタ係数である．
ウェーブレット関数を計算する：
ウェーブレット変換を実行する：

Le Gallのウェーブレット

Le Gallのウェーブレットを生成する．
ウェーブレットを初期化する：
特性を設定する：
"PrimalLowpass"特性と"DualLowpass"特性を定義する：
閾値にLe Gallウェーブレットを使う．
Le Gallウェーブレットを使ってStationaryWaveletTransformを実行する：