フロベニウス(Frobenius)方程式を解き,フロベニウス数を計算する
フロベニウス方程式とは以下の形式
を持った方程式のことである.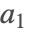 , …,
, …, 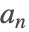 は正の整数,
は正の整数,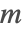 は整数であり,解の座標
は整数であり,解の座標 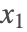 , …,
, …, 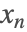 は非負の整数でなければない.
は非負の整数でなければない.
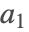 , …,
, …, 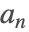 のフロベニウス数は,フロベニウス方程式
のフロベニウス数は,フロベニウス方程式 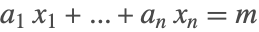 が解を持たなくなるような最大の整数
が解を持たなくなるような最大の整数 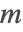 の値である.
の値である.
| FrobeniusSolve[{a1,…,an},b] | フロベニウス方程式 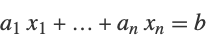 のすべての解のリストを返す のすべての解のリストを返す |
| FrobeniusSolve[{a1,…,an},b,m] | フロベニウス方程式 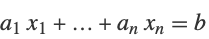 の の 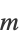 個の解を返す.解が 個の解を返す.解が 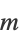 個ない場合は,すべての解を返す 個ない場合は,すべての解を返す |
| FrobeniusNumber[{a1,…,an}] | 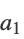 , …, , …, 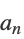 のフロベニウス数を与える のフロベニウス数を与える |
フロベニウス方程式を解きフロベニウス数を計算する関数
以下はフロベニウス方程式
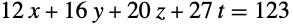
の解すべてを返す:
これは,フロベニウス方程式
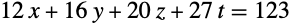
の解を1つ返す:
これは
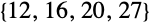
のフロベニウス数を求める.つまり,フロベニウス方程式
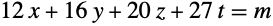
が解を持たないような最大の
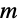
である:
次はフロベニウス方程式
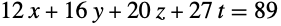
が本当に解を持たないことを示している:
1セント,5セント,10セント,25セントの硬貨を使って42セントにするすべての方法である:
24セント,29セント,31セント,34セント,37セント,39セントの切手を使うと,88セントより大きい任意の郵便料金が払える:
![]() , …,
, …, ![]() は正の整数,
は正の整数,![]() は整数であり,解の座標
は整数であり,解の座標 ![]() , …,
, …, ![]() は非負の整数でなければない.
は非負の整数でなければない.![]() , …,
, …, ![]() のフロベニウス数は,フロベニウス方程式
のフロベニウス数は,フロベニウス方程式 ![]() が解を持たなくなるような最大の整数
が解を持たなくなるような最大の整数 ![]() の値である.
の値である.