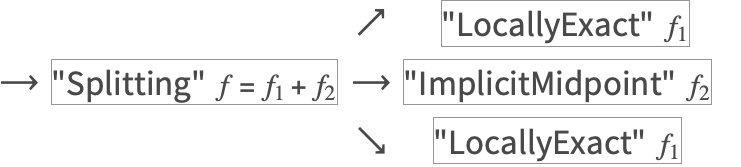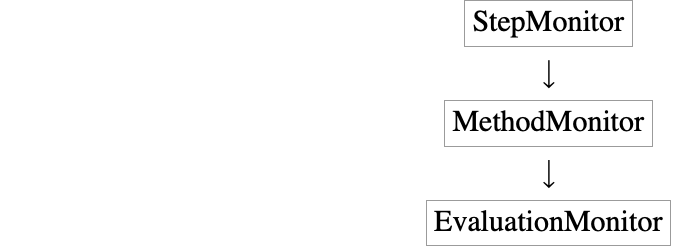NDSolveフレームワークの設計
機能
微分方程式の数値積分メソッドを多数サポートするのは大変なことである.
コードの維持や複製の手間を省くため,メソッド間では一般的な要素が共有されている.
このようなアプローチを取っているので,中央の2,3のルーチンでコードの最適化ができるようにもなっている.
NDSolveの枠組の主要な特徴は次の通りである.
- 最適化されたインプレース演算を使ってBLASモデル[LAPACK99]を一般化したものに基づいたベクトル化したフレームワーク
一般的な時間ステップ
すべてのワンステップのメソッドには一般的な時間ステップメカニズムが用いられている.このルーチンにより,以下を含む数多くの異なった基準が扱われる.
データの埋込み
各メソッドにはメソッドの呼出しに必要な情報を持った独自のデータオブジェクトがある.これには係数,作業領域,刻み幅を管理するパラメータ.刻み幅の受容/拒否のための情報,ヤコビ行列等が含まれるが必ずしもこれに限られない.これはLSODA ([H83], [P83])のようなコードで使われているアイディアを一般化したものである.
アルゴリズムの階層
メソッドはリエントラントで階層的になっている,つまり,ひとつのメソッドで他のメソッドを呼び出すことができる.これはC++で実装されている一般的なODEの解法システムGodess([O95],[O98]およびそれらに含まれる参考文献を参照のこと)で使われているアイディアを一般化したものである.
初期設計
当初のアルゴリズムのフレームワーク設計では,1つのソルバから数多くのアルゴリズムを呼び出すことができた.
NDSolve ⟶ "ExplicitRungeKutta"
NDSolve ⟶ "ImplicitRungeKutta"
改訂 1
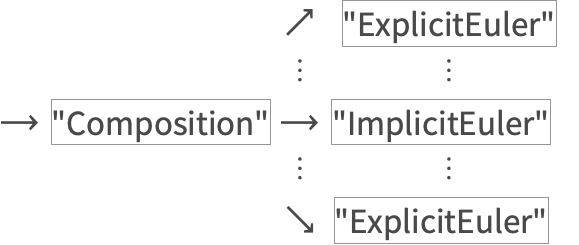
初期設計は後に,任意レベルのネスト構造を持つ連続的形式で,アルゴリズムから別のアルゴリズムが呼び出せるように拡張された.
NDSolve ⟶ "Extrapolation" ⟶ "ExplicitMidpoint"
NDSolve ⟶ "Projection" ⟶ "ExplicitRungeKutta"
改訂 2
合成メソッドを実装するために,さらに一般的な木構造の呼出しプロセスが必要となった.
現行
木構造の呼出しプロセスが拡張され,各メソッドを使って,ベクトル場全体ではなく部分体を解くことができるようになった.
この例は「NDSolveの合成・分割法」のサブセクションである「ABCフロー」に出てくる.
ユーザによる拡張
組込みのアルゴリズムを使って特殊目的の(合成)積分器のための有効なコンストラクト用のブロックを構築することができる.ユーザ定義のアルゴリズムを追加することもできる.
アルゴリズムのクラス
"ExplicitRungeKutta"のようなアルゴリズムは異なった次数のさまざまなスキームを含んでいる. また,ユーザがこれに代る係数を選択することもできる.これはRKSUITE [BGS93]に見られる考えを一般化したものである.
自動選択とユーザ側の操作性
このフレームワークは自動刻み幅選択とメソッド順選択を提供する.ユーザはメソッドオプションを使ってメソッドの設定が変更できる.
例えばユーザが"ExplicitRungeKutta"メソッドのクラスを選択したとする.するとコードが問題にとっての「最適な」順序,相対および絶対的な局所誤差の許容値,それに推定される初期刻み幅を自動的に確かめようとする.
以下は"ExplicitRungeKutta"の妥当なオプションのリストである.
MethodMonitor
硬さ切換えや,ランタイム時に起る次数変動等,あるメソッドの低レベルの動作を例示するため,新しい"MethodMonitor"が加わった.
これは"StepMonitor"の比較的大雑把な結果と,"EvaluationMonitor"の緻密な結果の間に位置する.
この機能は公には文書化されておらず,将来のバージョンでは機能に変更があるかもしれない.
共有機能
これらの機能は他の数値メソッドにも使えるもので,NDSolveに限られたものではない.
- 関数の評価はIEEE浮動小数点のオーバーフローやアンダーフロー等の際に必要に応じてタイプを動的に変更するNumericalFunctionを用いて行われる.また,これは必要に応じてWolfram言語のコンパイラであるCompileを効率化のために呼び出す.
- この他に実装されているサポート機能については「NDSolveのノルム」で説明する.
いくつかの基本的なメソッド
次数
|
メソッド
|
式
|
| 1 | 前進オイラー法 | 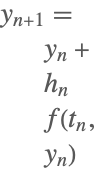 |
| 2 | 陽的中点公式 | 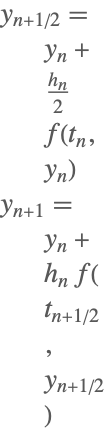 |
| 1 | 後退オイラー法(1段RadauIIA) | 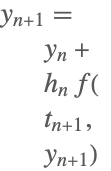 |
| 2 | 陰的中点公式(1段ガウス) | 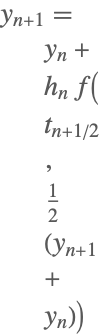 |
| 2 | 台形公式(2段Lobatto IIIA) | 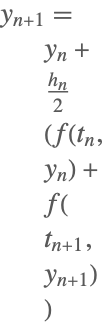 |
| 1 | 陰的線形オイラー法 | 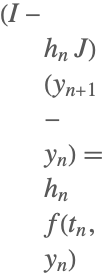 |
| 2 | 陰的線形中点法 | 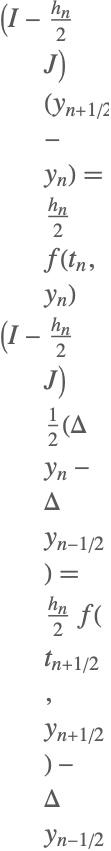 |
ここで![]() が成り立ち,
が成り立ち,![]() は単位行列を,
は単位行列を,![]() はヤコビ行列
はヤコビ行列 ![]() をそれぞれ意味する.
をそれぞれ意味する.
陰的中点法は独立したメソッドとしては実装されていないが,"ImplicitRungeKutta"メソッドの一段ガウス(Gauss)スキームで使用することができる.