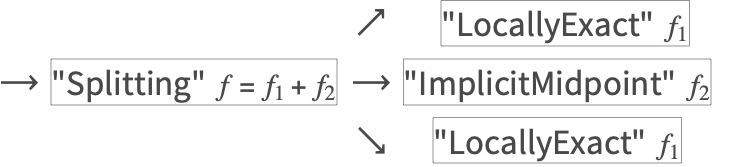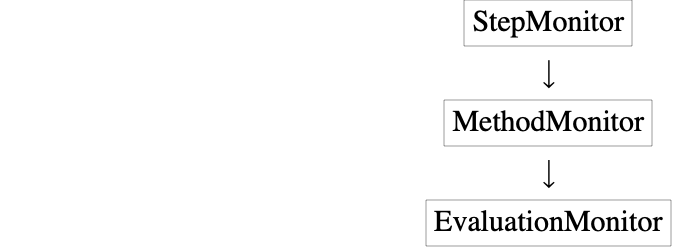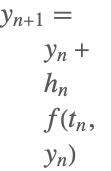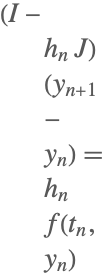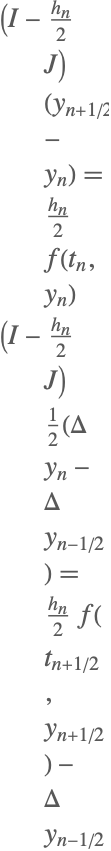NDSolve 框架设计

特点方法类
共同的时间步进自动选择和用户可控性
数据封装MethodMonitor
方法层级共享特色
用户扩展性一些基本方法

特点

支持大量微分方程的数值积分方法花费很多工作.

为了减少维护和代码复制的代价，通用的成分在方法之间是共用的.

这种方法还允许代码的优化只在几个中心例程中进行.

NDSolve 框架的主要特点是：

共同的时间步进

一个共同的时间步进的机制用于所有一步的方法. 该程序处理大量不同的指标，包括：

数据封装

每种方法都有自己的包含该方法调用所需信息的数据对象. 这包括，但不限于，系数、工作区、步长控制参数、步长接受/拒绝信息，以及雅可比矩阵. 这是用于像 LSODA 这样的代码中的思想的推广（[H83], [P83]）.

方法层级

方法是可重入的，并且具有层级的，这意味着一个方法可以调用另一个. 这是用于一般常微分方程 （ODE） 求解系统，即Godess （见 [O95]、[O98] 和所附的参考文献）的思想的推广，它用 C++ 实现.

初始设计

原有的方法框架允许大量方法在求解器中被调用.

NDSolve ⟶ "ExplicitRungeKutta"

NDSolve ⟶ "ImplicitRungeKutta"

第一次修订

这在后来被扩展到允许一个方法以顺序方式，按照任意数量的嵌套，调用另一个方法.

NDSolve ⟶ "Extrapolation" ⟶ "ExplicitMidpoint"

复合积分方法的构建对于几何数值积分特别有用.

NDSolve ⟶ "Projection" ⟶ "ExplicitRungeKutta"

第二次修订

需要一个更普遍的树调用过程来实现组成方法.

NDSolve

这是一个由连接方法组成的方法的例子.

当前状态

扩展了树的调用过程，以允许由每个方法求解子场，而不是整个向量场.

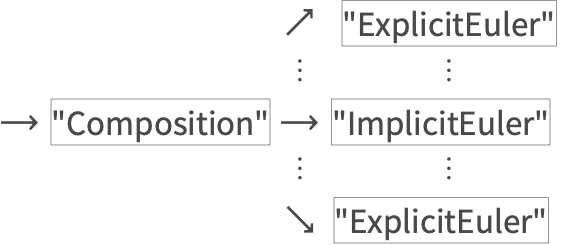
这个例子出现在 "NDSolve 的 "Composition" 和 "Splitting" 方法" 的ABC流章节中.

NDSolve

用户扩展性

内置方法可以用作特殊用途（复合）积分器的有效构建的组成块. 也可以添加用户定义的方法.

方法类

诸如 "ExplicitRungeKutta" 等的方法包括大量不同阶数的方案. 此外，不同的系数选择也可以由用户指定. 这是在RKSUITE 中的思想的推广 [BGS93].

自动选择和用户可控性

该框架提供自动步长选择和方法顺序选择. 方法可由用户通过方法选项来配置.

例如，用户可以选择一类 "ExplicitRungeKutta" 方法，代码将根据问题、相对和绝对局部误差容差和初始步长估计，自动尝试确定“最优”的阶数.

下面是适用于 "ExplicitRungeKutta" 的一个选项列表.    

MethodMonitor

为了说明一些方法的底层行为，如刚性切换或者运行时的阶数变化，已经加入一个新的 "MethodMonitor".

它介于相对粗糙的 "StepMonitor" 解决方法和优良的 "EvaluationMonitor" 解决方案之间.

此功能没有正式编档，并且这些功能在未来版本中可能会改变.

共享特色

这些特点并不一定局限于 NDSolve，因为它们也可以用于其它数值方法.

一些基本方法

顺序
方法
公式
1显式欧拉
2显式中点
1反向或者隐式欧拉（1-阶段 RadauIIA）
2隐式中点（1-阶段高斯）
2梯形 （2-阶段 Lobatto IIIA）
1线性隐式欧拉
2线性隐式中点

已经实现的一些一步方法.

这里 ， 表示单位矩阵，而 表示雅可比矩阵 .

虽然隐式中点法尚未作为一个单独的方法实现，但是它可以通过 "ImplicitRungeKutta" 方法的一阶段高斯方案得到.