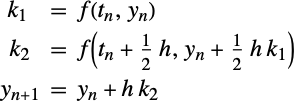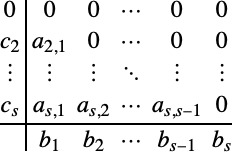NDSolveの"ExplicitRungeKutta"メソッド

はじめに硬さ
例題硬さ検出
メソッドの比較刻み幅制御再考
係数プラグインオプションの要約
メソッドプラグイン

はじめに

検定問題と効用関数を含むパッケージをロードする：

オイラー(Euler)法

初期値問題を解くための初期の最も簡単なメソッドに，オイラーによって提唱されたものがある．

しかし，オイラー法はあまり正確ではない．

局所的な精度は，高次項が解のテイラー(Taylor)展開とどの程度マッチしているかによって測定される．オイラー法は一次精度なので，誤差は一次高く というベキ乗から始まる．

オイラー法は"ExplicitEuler"としてNDSolveに実装されている：

オイラー法の一般化

ルンゲ・クッタ(Runge–Kutta)法の考えは，連続した（重み付き）オイラー法によるステップでテイラー級数を近似するというものである．関数の評価（導関数ではない）は以下のように使われる．

一段の中点公式を例に取る：

中点公式には という局所誤差があることが示されるので，これは二次精度である．

中点公式は"ExplicitMidpoint"としてNDSolveに実装されている：

ルンゲ・クッタ法

(1)のアプローチを拡張すると，関数評価を繰り返すことでさらに高次のメソッドを求めていくことができる．

における初期値問題の近似解に対するルンゲ・クッタ法は以下のように表わされる．

ここで は段数である．

一般に，行要素の和の条件によって以下が成り立つとされる．

この条件は，関数が抽出される時間の点を実質上決定する．これは高次のルンゲ・クッタ法の導出では，特に便利な手段である．

ルンゲ・クッタ法の係数は，時間刻み のある次数までのテイラー級数展開を満足するように選ばれる自由パラメータである．実際には，係数は安定性等の他の条件によっても制約される．

陽的ルンゲ・クッタ法は，行列 が厳密に下三角行列であるときの特殊形である．

ルンゲ・クッタ法の係数は以下の表を使って ，，と表すことが慣習となっている．陽的ルンゲ・クッタ法の係数の表は以下の形式である．

行要素の和の条件は，表の行の要素すべてを加算することで可視化できる．

陽的である結果は となるので，関数は現在の積分ステップの最初に抽出されるという点に注目する．

例題

陽的中点法(2)の係数の表は以下のように与えられる．

FSALスキーム

陽的ルンゲ・クッタ法の特に興味深い特殊クラスに，係数にFSAL（First Same As Last：最初と最後が同じ）として知られる特殊構造を持つものがある．このクラスは最近のほとんどのコードで使用されている．

矛盾のないFSALスキームでは係数表(3)は以下の形式となる．

FSAL法の長所は，1つの積分ステップの最後の関数値 が次の積分ステップの最初の関数値 と同じであるという点である．

各積分ステップの最初と最後の関数値は，いずれにせよNDSolveの緻密な出力に使われるInterpolatingFunctionの構築時に必要となるものである．

埋め込まれたペアの公式と局所誤差推定

適応刻み幅制御の局所誤差推定を得るためには，同じ係数行列（および関数値）を持つ異なる次数 および の2つのメソッドを考慮すると効率的である．

以下には2つの解がある．

一般的に使われる表記は で，通常 あるいは である．

NDSolveのデフォルトコードを含む最近のほとんどのコードでは，解は が成り立つようなより正確な公式を使って求められる．これは局所的な外挿として知られている．

係数のベクトル は(4)と(5)の差分を形成する際に，浮動小数点演算において の減算による桁落ちを避ける誤差推定量を与える．

数量は刻み幅の選択に使うことができる誤差のスカラー量である．

刻み幅

古典的な積分（I）制御，すなわち積分刻み幅制御では以下の公式を使う．

ここで である．

つまり，現行の刻み幅から次の刻み幅を決定するために誤差推定が使われる．

という表記については「NDSolveのノルム」で説明してある．

概要

二次(1)から九次(8)までの陽的ルンゲ・クッタ法のペアが実装されている．

公式のペアは以下のような属性を持つ．

例題

まず，化学反応をモデル化するブラッセレータ(Brusselator)の常微分方程式問題を定義する：
次に，陽的ルンゲ・クッタを使ってこの系を解く：
解から補間関数を抽出する：
解の要素をプロットする：

メソッドの比較

時として，NDSolveで使われているメソッドが知りたい場合があるかもしれない．

以下のようにすると，デフォルトの二次(1)の埋め込み型公式ペアの係数を見ることができる：

ある特定の問題に対してどのメソッドが効果的か，いくつかのメソッドを比較してもよいだろう．

効用関数

さまざまなメソッドを比較するためには効用関数のCompareMethodsを利用する．この関数には，メソッドの比較に使える以下の便利なNDSolve機能がある．

参照解

文献に見られる数値法の比較例の多くは，閉形式の解が利用できるということに依存するため，非常に制約があることは明らかである．

NDSolveでは，"Extrapolation"に基づく次数の適応法である任意精度の適応刻み幅を使って，非常に正確な近似を得ることが可能である．

以下の参照解は，問題の系が硬いかどうかによって"Extrapolation"法のペアのいずれかに切り換えるメソッドで計算される：

自動次数選択

"DifferenceOrder"->Automaticと選択すると，コードはその積分に対して最適次数のメソッドを自動的に選ぼうとする．

このために2つのアルゴリズムが実装されている．これらについては，「NDSolveのSymplecticPartitionedRungeKutta法」で説明してある．

例題　1

以下はさまざまな次数の組込みメソッドおよび自動選択メソッドを比較する例である．

以下でどちらのメソッド次数を使うかを選び，NDSolveに渡すメソッドオプションのリストを作成する：
積分ステップ数，関数評価回数，大域的な終点誤差を計算する：
結果を表で示す：

デフォルト次数は9であり，この例では最適次数の8に近い．次数を決定するためには，初期化段階で関数を1回評価する必要がある．

例題　2

例題1では，各メソッドによって得られた解の確度を考慮に入れないため，コストを妥当に反映しないという制限がある．

メソッドを比較するためには，単一の許容誤差を取るよりも許容誤差の範囲を使った方がよい．

以下の例では，さまざまな許容誤差を使った異なる次数の"ExplicitRungeKutta"メソッドを比較してみる．

以下は，どちらのメソッド次数を使うかを選び，NDSolveに渡すメソッドオプションのリストを作成する：
確度と作業とを比較するデータは，許容範囲でCompareMethodsを使って計算する：
さまざまなメソッドでの作業-誤差の比較データが以下にプロットされている．ここで，大域的誤差は縦軸に，関数評価の回数は横軸に表示されている．選ばれたデフォルト次数（赤で表示）は，許容誤差が増加するに従って増加していることが分かる：

次数選択のアルゴリズムは，最適次数が積分過程で変化する可能性があるという点でヒューリステックである．しかし，上の例のように，通常デフォルトは妥当に選択される．

ベンチマークには異なる問題を選択することが理想的である．

係数プラグイン

"ExplicitRungeKutta"を実装すると，各次数のデフォルトメソッドのペアが提供される．

しかし，以下のような場合は異なるメソッドを使った方が便利なことがある．

古典的ルンゲ・クッタ法

以下は，精度 に近似された陽的な古典的ルンゲ・クッタ四次法の係数を定義する方法である：

このメソッドには埋込みの誤差推定がないので，係数の誤差ベクトルの指定がない．つまり，このメソッドは固定刻み幅で使われるということである．

以下は，呼び出し文法の例である：

ode23

ここではFSALスキームを持つ陽的ルンゲ・クッタ三次法(2)ペアの係数を定義する．

三次公式はRalstonによるものであり，埋込み型公式はBogackiとShampine[BS89a]によって導かれたものである．

以下は係数を希望の精度まで計算する関数を定義する：

このメソッドはTexas Instruments TI-85のポケット電卓，Matlab，RKSUITE [S94]で使われている．残念ながらこのメソッドでは，選ばれた硬さ検出形式が使えない．

フェールベルク(Fehlberg)法

ここでは，1960年代に人気のあったルンゲ・クッタ-フェールベルク四次法(5)[F69]の係数を定義する．

四次公式は解を伝播するために，五次公式は誤差推定のためだけに使用される．

以下は係数を希望の精度まで計算する関数を定義する：

四次の古典的ルンゲ・クッタ法とは対照的に，係数には誤差推定に使われる追加項目が含まれている．

フェールベルク法は，その係数行列が(6)の形式ではないため，FSALスキームではない．これは六段スキームであるが，InterpolatingFunctionを構築するステップの最後で必要とされる関数評価があるため，ステップ毎に6回の関数評価が必要である．

Dormand–Prince法

以下はDormand–Prince係数[DP80]五次(4)法のペアを定義する方法である．これは現在Matlabのode45で使われているメソッドである．

以下は係数を希望の精度まで計算する関数を定義する：

Dormand–Prince法は係数行列が(7)の形式になるので，FSALスキームである．これは七段スキームであるが実質的には6回の関数評価しか使わない．

組込みの係数の代りにDormand–Princeの係数を使う方法である．この係数の構造には誤差ベクトルが含まれるので，これを実装することで適応刻み幅の計算が保障される：

メソッドの比較

ここでは陽的ルンゲ・クッタ法のペアをいくつか使って系を解いてみる．

フェールベルク五次法(5)のペアでは，埋込み公式の次数を指定するのに"EmbeddedDifferenceOrder"オプションが使われる：
Dormand-Prince五次法(4)ペアは以下の通り定義される：
BogackiとShampineの五次法(4)ペアはデフォルトの五次法である：
メソッド名とその記述名をリストに入れる：
積分ステップ数，関数評価回数，大域的な終点誤差を計算する：
結果を表で示す：

デフォルトのメソッドのコストが最小で，しかも，最も正確な解を与えている．

メソッドプラグイン

ここではメソッドプラグイン環境を使って，古典的な陽的ルンゲ・クッタ四次法を実装する方法を示す．

このメソッドは事実上データを持たないため，以下の定義はオプションである．しかし，どのような式もデータオブジェクト内部に保存することができる．例えば，各積分ステップで係数が有理数から浮動小数点数に強制されることを避けるために，ここでは係数を近似することができる：
実際のメソッドの実装は，ステップの手続きを使って書かれる：

この実装は，教科書等で見られる記述と非常に似ていることに注目されたい．例えば，メモリの割当てや割当て解除文，あるいは型の宣言がないという点である．この実装は機械実数と機械複素数の他，任意精度のソフトウェア演算を使っても動作する．

以下は呼び出し文法の例である．簡単にするために，メソッドは固定刻み幅のみを使用するようにしてあるので，その刻み幅を指定する必要がある：

NDSolveに組み込まれているメソッドの多くは，効率を上げるため，カーネルに実装される前に，まずトップレベルのコードを使ってプロトタイプ化される．

硬さ

硬さとは問題，初期データ，数値法，許容誤差の組合せである．

例えば，差分商による拡散項を大規模な常微分方程式系に変換すると，硬さが生じることがある．

硬さの性質について理解を深めるためには，メソッドが簡単な問題に適用された場合にどのように動作するかを調べるのが有効である．

線形安定

ここでは，ルンゲ・クッタ法をダールキスト(Dahlquist)の方程式として知られる線形スカラー方程式に適用してみる．

その結果は，多項式の有理関数 （ここで ）となる（[L87]等を参照のこと）．

この効用関数でルンゲ・クッタ法の線形安定関数 を求める．形式は係数に依存しており，ルンゲ・クッタ法が陽的であれば多項式となる．

以下はDormand–Prince五次法(4)ペアの五段スキームの安定関数である：

この関数はルンゲ・クッタ法の線形安定関数 を求める．形式は係数に依存しており，ルンゲ・クッタ法が陽的であれば多項式となる．

このパッケージは，微分方程式の数値法の線形安定領域を視覚化するのに便利である：
これで絶対安定領域が可視化できるようになった：

(8)の の大きさ次第では，となるように刻み幅 を選ぶと，連続したステップの誤差が小さくなる．このときメソッドは「絶対安定」であると言われる．

であれば，刻み幅の選択は局所的な精度ではなく，安定性によって制限される．

硬さ検出

オプション"StiffnessTest"で使われる硬さ検出の手法については，「NDSolveのStiffnessTestメソッドオプション」で説明している．

陽的ルンゲ・クッタ法で硬さ検出の条件を再計算すると，以下の公式になる．

ここで と は(9)の定義による．

差分 は に適用されるベキ乗法の適用回数に対応して示すことができる．

従って，差分は最初の固有値に対応する固有べクトルによく近似している．

積 は硬さを検出するために，安定境界と比較できる推定を与える．

とすると， 段の陽的ルンゲ・クッタは(10)に適した形式を持つ．

"ExplicitRungeKutta"で使われるデフォルトの埋込み公式ペアはすべて形式(11)である．

ここで重要なのは，(12)は非常にコストが低く便利であるという点である．これは積分からのすでに利用可能な情報を使い，それ以上の関数評価を必要としない．

(13)のもうひとつの利点は，矛盾のないFSAL法(14)を利用するのが簡単であるという点である．

例題

化学反応をモデル化する硬い系を選ぶ：

以下で組込みの陽的ルンゲ・クッタ法をその硬い系に適用する．

硬さ検出は，実行時間にあまり影響を及ぼさないので，デフォルトで動作するようになっている：
Dormand–Prince五次法(4)ペアの係数は(15)の形式を取るので，硬さ検出は有効になる：
特性"LinearStabilityBoundary"が指定されていないので，デフォルト値が選ばれる．この場合，値は次数5の汎用メソッドに対応する：
線形安定関数の方程式を設定し，それを厳密に解くことによって曲線が負の実数軸と交差する点を求めることができる：
デフォルトの汎用値は計算された値よりもその大きさが僅かに小さい：

一般に交点は2つ以上あることがあるので，適切な解を選ぶ必要がある．

以下の定義は線形安定境界の値を設定する：
この例に新しい値を使っても，硬さが検出される時間には影響しない：

なので，四次フェールベルク法(5)には硬さ検出に必要な正しい係数構造(16)がない．

デフォルト値"StiffnessTest"->Automaticは，メソッドの係数が硬さ検出機能を提供するかどうか，また，提供する場合はそれが動作するようになっているかどうかをチェックする．

刻み幅制御再考

適度に硬い系の問題を考慮する際に，標準的なI制御(17)に代るものを探すのにはそれなりの理由がある．

以下の系は化学反応をモデル化する：
以下は硬さ検出を使わないDormand–Prince係数に基づく陽的ルンゲ・クッタ法を定義する：
以下でその系を解き，効用関数StepDataPlotを使って刻み幅をプロットする：

硬い系の問題，あるいは適度に硬い系の問題を標準的な刻み幅制御を使って解くと，振動が大きくなる．時には好ましくない刻み幅の拒絶が多く起ってしまう．

この問題の研究は，「刻み幅制御の安定性」として知られている．

この問題は，埋め込まれた公式ペアの高次法および低次法の線形安定領域をマッチさせて調べることができる．

振動を避けるひとつの方法として，特殊なメソッドを導くということが挙げられるが，これでは局所的な精度を諦めることになる．

PI制御

I制御(18)に代る方法として，PI制御というものがある．

この場合，公式に従って，2つの連続した積分ステップにおける局所誤差を使って刻み幅が選ばれる．

これには減衰効果があるため，刻み幅のシーケンスがスムーズになる．

I制御(19)は(20)の特殊形で，ステップが拒絶されたときに使われることに注意する．

k1と k2の値を指定するときは，オプション"StepSizeControlParameters"->{k1,k2}を使うことができる．

(21)でスケールされた誤差推定は，最初の積分ステップではとなる．

例題

硬い系の問題

ここではPI制御を指定する"StepSizeControlParameters"オプションを使うIERKに似たメソッドを定義する．

まず，Gustafssonによって提案された汎用制御パラメータを使う．

以下はステップ制御パラメータを指定する：
再び系を解くと，一連の刻み幅がずっとスムーズになったのが分かる：

硬くない系の問題

以下に示すように，一般にI制御(22)は硬くない系の問題に対してPI制御(23)よりも大きい刻み幅を取ることができる．

Iステップ制御を使って，硬くない系を解く：
PI制御を使うと，刻み幅はわずかに小さくなる：

上記の理由で，"StepSizeControlParameters"のデフォルト設定はAutomaticとなっており，これは以下のように解釈される．

微調整

(26)を直接使う代りに安全因子を使って，誤差が次のステップで高い確率で受容されるようにすることがよくある．これだと，ステップの拒絶を防ぐことができる．

オプション"StepSizeSafetyFactors"->{s1,s2}は(27)が以下のようになるよう，刻み幅推定で使う安全因子を指定する．

ここで s1は絶対因子，s2は通常メソッドの次数でスケールされる．

オプション"StepSizeRatioBounds"->{srmin,srmax}は以下のようになるよう次の刻み幅の範囲を指定する．

オプションの要約

オプション名
デフォルト値
"Coefficients"EmbeddedExplicitRungeKuttaCoefficients陽的ルンゲ・クッタ法の係数を指定する
"DifferenceOrder"Automatic局所的な確度の次数を指定する
"EmbeddedDifferenceOrder"Automatic陽的ルンゲ・クッタ法1ペアの中の埋め込まれたメソッドの次数を指定する
"StepSizeControlParameters"AutomaticPI制御パラメータ（(28)を参照）を指定する
"StepSizeRatioBounds"{,4}新しい刻みは場の相対変化の限界（(29)を参照）を指定する
"StepSizeSafetyFactors"Automatic刻み幅推定で使う安全因子（(30)を参照）を指定する
"StiffnessTest"Automatic硬さ検出機能を使うかどうかを指定する

"ExplicitRungeKutta"法のオプション

オプション"DifferenceOrder"のデフォルト設定Automaticでは，問題，初期値，局所誤差許容度に基づき，各係数集合に対するメソッドの仕事に対して均衡を取り，デフォルトの係数次数が選ばれる．

オプション"EmbeddedDifferenceOrder"のデフォルト設定Automaticでは，埋め込まれたメソッドのデフォルトの次数はメソッドの次数より1つ低くなるよう指定される．これは"DifferenceOrder"オプションの値に依存する．

オプション"StepSizeControlParameters"のデフォルト設定Automaticでは，硬さ検出が有効なときには値{1,0}が，それ以外では{3/10,2/5}が使われる．

オプション"StepSizeSafetyFactors"のデフォルト設定Automaticでは，Iステップ制御(31)が使われているときは値{17/20,9/10}が，PI制御(32)が使われているときは値{9/10,9/10}が使われる．使用される刻み幅制御は，オプション"StepSizeControlParameters"および"StiffnessTest"の値に依存する．

オプション"StiffnessTest"のデフォルト設定Automaticは，係数が形式(33)を持つ場合，そのときに限り硬さ検出テストを有効にする．