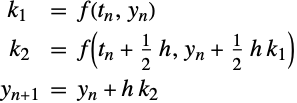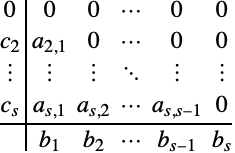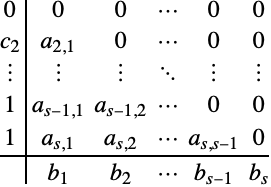NDSolve 的 “ExplicitRungeKutta” 方法

引言刚性
示例刚性检测
方法比较再论步长控制
系数插入（Coefficient plug-in）选项总结
方法插入（Method Plug-in）

引言

以下加载包含一些测试问题和功用函数的程序包：

欧拉方法

求解初值问题的第一个以及最简单的方法之一由欧拉提出：

欧拉方法不是很准确.

局部准确性是由多么高阶项与解的泰勒展开的匹配来衡量的. 欧拉方法是一阶准确的，因此误差从高一阶即 的幂开始出现.

欧拉方法在 NDSolve 中以 "ExplicitEuler" 实现：

欧拉方法的推广

朗格-库塔方法的思想是采用连续（加权）的欧拉步骤来对一个泰勒展开进行近似. 在这种方式下，使用的是函数计算（而非导数）.

例如，考虑中点法 的一步公式：

可以证明，中点法具有 的局部误差，因此，它是二阶准确的.

中点法在 NDSolve 中以 "ExplicitMidpoint" 实现：

朗格-库塔方法

作为对 (1) 中的方法进行扩展，可以使用重复函数计算以获取高阶方法.

把在 处的一个初值问题的近似解的朗格-库塔方法表示为：

其中 是阶段数目.

一般地，假设行-和条件（row-sum conditions）成立：

这些条件实际上确定了函数被采样的时间点，在推导高阶朗格-库塔方法上是一个特别有用的工具.

方法的系数是为了在时间步骤 中满足某个阶数的泰勒展开而选择的自由参数. 在实际应用中，其它条件，比如稳定性也可以限制这些系数.

显式朗格-库塔方法是一个矩阵 具有严格的下三角结构的特殊的情况：

使用一个 Butcher 表格来表示方法系数 、 和 已经成为一种惯例，它对于显式朗格-库塔方法具有如下格式：

行-和条件可以作为表格的行上的和来可视化.

注意，显式的结果是 ，因此函数在当前积分步骤的开始时被采样.

示例

显式中点法（1）的 Butcher 表格如下：

FSAL 方案

显式朗格-库塔方法的一个特别有趣的，用于大部分现代代码的特殊类型，是系数具有一种称为 First Same As Last （FSAL）的特殊结构的类型：

对于具一致性的 FSAL 方案，Butcher 表格（2）具有如下形式：

FSAL 方法的优点是在一个积分步骤末尾的函数值 与下一个积分步骤的第一个函数值 相同.

当构建用于 NDSolve 中稠密输出的 InterpolatingFunction 时，要用到在每个积分步骤的开始和末尾的函数值.

嵌入对和局部误差估计

一个用于自适应步长控制的获取局部误差估计的有效方法是考虑具有不同阶数 和 的两种方法，它们共享同样的系数矩阵（因而同样的函数值）.

这里给出两个解：

一个广泛被使用的记号是 ，通常 或者 .

在大部分现代代码中，包括在 NDSolve 中的默认选择，解是使用更准确的公式推进的，因而有 ，这被称为局部外插法.

系数的向量 给出了一个误差估计器，以避免在计算(3) 和 (4) 之间的差异时，在浮点运算中 的减法相消 .

量 给出了一个可用于步长选择的误差的标量度量.

步长控制

典型积分（或者 I）步长控制器使用公式：

其中 .

因而，误差估计用来从当前步长决定下一个步长.

记号 在 "NDSolve 中的范数" 中有解释.

概况

阶数从 2(1) 到 9(8) 的显式朗格-库塔对已经被实现.

公式对具有如下属性：

示例

定义 Brusselator 常微分问题，它对一个化学反应建模：
以下使用一个显式朗格-库塔方法求解该系统：
从解中提取插值函数：
画出解的组成部分的图形：

方法比较

有时候，用户可能有兴趣找出在 NDSolve 中使用了什么方法.

下面可以看到默认的 2(1) 嵌入对的系数：

用户还可能要比较一些不同的方法，看看它们对一个特定问题表现如何.

功用函数（Utilities）

用户可以使用一个功用函数 CompareMethods 来比较不同方法. 该函数用于比较方法的一些有用的 NDSolve 特征为：

参考解

在文献中的用于数值方法比较的大量例子依赖于一个事实，即存在一个解析解，这显然是相当有限的.

在 NDSolve 中，有可能使用任意精度自适应步长，得到非常准确的近似值；这是都是基于 "Extrapolation" 的自适应阶数方法.

下面参考解使用在一对 "Extrapolation" 方法之间切换的方法来计算，切换取决于该问题是否是刚性的：

自动阶数选择

当用户选择 "DifferenceOrder"->Automatic，该代码将自动尝试为积分选择最优阶数方法.

为了实现该目的，已经有两个算法被实现，并且在 "NDSolve 的 SymplecticPartitionedRungeKutta 方法" 中有描述.

示例 1

下面的例子是和自动选中的方法一起，比较不同阶数内置方法.

这里选择待选用方法的阶数，并且生成一个传给 NDSolve 的方法选项的列表：
计算积分步骤的数目、函数计算和端点全局误差：
在一个表格中显示结果：

该默认方法具有阶数9，它与本例中8个阶数中的最优阶数相近. 在初始化阶段，需要一个函数计算来决定阶数.

示例 2

前面的例子的一个局限是它没有考虑由每个方法得到的解的准确性，因此它没有给出对成本的公平的反映.

与采用一个单一的容差来比较方法相反，最好使用一定范围的容差.

下面的例子是使用各种容差来比较具有不同阶数的各种 "ExplicitRungeKutta" 方法.

这里选择待选用方法的阶数，并且生成传递给 NDSolve 的方法选项的一个列表：
对一定范围的容差，使用 CompareMethods 来计算比较准确度和工作量的数据：
下面对数坐标图中显示了各种方法的工作量-误差比较数据，其中全局误差显示在纵轴上，而函数计算的数目显示在横轴上. 可以看出，选中的默认阶数（显示为红色）随着容差增而增加：

最优阶数在积分中可能会变化，从这一点讲，阶数选择算法是试探式的，但是正如例子所示，通常它会做一个合理的默认选择.

理想情况下，不同问题的选择应该用来作为基准.

系数插入（Coefficient plug-in）

"ExplicitRungeKutta" 的实现在每个阶数提供了一个默认方法对.

不过，有时候，使用一个不同的方法是方便的，例如：

经典朗格-库塔方法

下面显示如何定义四阶经典显式朗格-库塔方法的系数，近似到精度 ：

该方法不具有嵌入式误差估计，因此没有系数误差向量的规格. 这意味着该调用方法时使用固定步长.

下面是调用语法的一个例子：

ode23

这里定义一个 3(2) FSAL 显式朗格-库塔对的系数.

该三阶公式由 Ralston 提出，而嵌入式方法由 Bogacki 和 Shampine 导出[BS89a].

这里定义一个函数，以计算系数到一个预期的精度：

该方法用于德州仪器TI-85袖珍计算器（Texas Instruments TI-85 pocket calculator）、Matlab 和 RKSUITE 中 [S94]. 遗憾的是，它不允许已经选定的刚性检测的形式.    

一个Fehlberg 方法

下面定义在六十年代流行的Fehlberg的一个 4(5) 显式朗格-库塔对的系数 [F69].

四阶公式用于传播解，而五阶公式只用于误差估计.

下面定义函数用以把系数计算到一个预期的精度：

与四阶经典朗格-库塔方法相反，该系数包含用于误差估计的额外项.

该 Fehlberg 方法不是一个 FSAL 方案，因为系数矩阵不具有形式 (5)；它是一个六阶段方案，但是在每步都需要六个函数计算，因为在步骤末尾需要函数计算以构建 InterpolatingFunction.

一个 Dormand-Prince 方法

下面显示如何定义 Dormand 和 Prince 系数的一个 5(4) 对[DP80]. 这是目前在Matlab中 ode45 所使用的方法.

下面定义一个函数，来计算系数到一个预期的精度：

Dormand–Prince方法是一个 FSAL 方案，因为系数矩阵具有形式 (6)；它是一个七阶段方案，但是实际上只使用六个函数计算.

以下显示Dormand 和 Prince 的系数可以如何使用来代替内置选择. 因为系数的结构包括一个误差向量，实现方法能够确定自适应步长可以计算：

方法比较

这里用户可以使用一些显式朗格-库塔对求解一个系统.

对于 Fehlberg 4(5) 对，使用选项 "EmbeddedDifferenceOrder" 来指明嵌入式方法的阶数：
Dormand 和 Prince 5(4) 对的定义如下：
Bogacki 和 Shampine 的 5(4) 对是默认的五阶方法：
把方法和一些描述名称一起放入一个列表中：
计算积分步骤的数目、函数计算和端点全局误差：
把结果在一个表格中显示：

默认方法的代价最低，并且提供了最准确的解.

方法插入（Method Plug-in）

这里显示如何使用方法插入环境实现经典四阶显式朗格-库塔方法.

这个定义是可选的，因为事实上该方法没有任何数据. 但是，任何表达式都可以存储在数据对象中. 例如，这里系数可以近似，以避免在每个积分步骤从有理数到浮点数的强制转换：
实际方法实现是使用一个步进程序编写的：

请注意，该实现方法与在一本教科书中可能找到的描述非常相似. 例如，这里没有内存分配/释放语句或者类型声明. 事实上，该实现对于机器实数或者机器复数都适用，甚至对于使用任意精度的软件算法也适用.

以下是调用语法的一个例子. 为了简单起见，该方法只使用固定步长，所以用户需要指定采用哪些步长：

为了提高效率，在内核中实现之前，在 NDSolve 中内置的许多方法首先使用顶层代码原型化.

刚性

刚性是问题、初始数据、数值方法和误差容差的一个组合.

例如，刚性可以出现在把扩散项通过差分(divided differences)翻译成一个大型常微分方程组中.

为了对刚性的本质有更深的理解，研究当应用于一个简单问题时方法如何表现是有用的.

线性稳定性

考虑把朗格-库塔方法应用到一个称为 Dahlquist 方程的线性标量方程中：

结果是一个由多项式 组成的有理函数，其中 （例如，参阅 [L87]）.

该功用函数找到了朗格-库塔方法线的性稳定性函数 . 其形式取决于系数，并且如果朗格-库塔方法是显式的话，是一个多项式.

以下是 Dormand–Prince 5(4) 对中五阶方案的稳定性函数：

该函数找到了朗格-库塔方法的线性稳定性函数 . 该形式取决于系数，并且如果朗格-库塔方法是显式的话，是多项式的.

下面程序包对于微分方程的数值方法的线性稳定性区域的可视化是很有帮助的：
用户现在可以可视化绝对稳定性区域 ：

取决于（7）中 的大小，如果用户选择步长 使得 ，那么，后续步骤中的误差将会衰减，该方法可以说是绝对稳定的.

如果 ，那么步长选择将受稳定性限制，而不受局部准确性限制.

刚性检测

与选项 "StiffnessTest" 一同使用的刚性检测的设备在 "刚性检测" 中得到描述.

用显式朗格-库塔方法的形式来重写，刚性检测条件可以表示为：

其中 和 在（8）中定义.

可以证明，差值 对应于应用于 的幂方法（power method）的大量应用.

因此，差值是对应于主导特征值的特征向量的很好的近似.

为了检测刚性，积 给出可以与稳定性边界相比较的一个估计.

如果 ，一个 -阶段显式朗格-库塔具有适用于（9）的形式.

在 "ExplicitRungeKutta" 中使用的默认嵌入对都具有形式（10）.

重要的一点是：（11）代价很低而且很方便；它使用积分的已有信息，不需要额外的函数计算.

(12) 的另一个优点是它直接使用一致 FSAL 方法 (13).

示例

选择一个刚性系统，对一个化学反应建模：

这里把一个内置显式朗格-库塔方法应用到刚性系统.

默认情况下，刚性检测是激活的，因为它对运行时间只有很小的影响：
Dormand–Prince 5(4)对的系数具有形式（14 ），所以刚性检测激活的：
因为没有指定 "LinearStabilityBoundary" 属性，一个默认值被选用. 在这种情况下，该值对应于阶数为 5 的一个通用方法：
用户可以用线性稳定性函数的形式建立一个方程，并且精确地对它进行求解，以找到等高线穿过负实轴的点：
默认通用值在大小上比计算所得值略小：

一般来说，可能有一个以上的交叉点，因而它可能有必要选择合适的解.

下面定义设置了线性稳定性边界的值：
对该例子使用新值不影响刚性检测的时间：

Fehlberg 4(5) 方法没有刚性检测所要求的正确系数结构（2），因为 .

默认值 "StiffnessTest"->Automatic 检查方法系数是否提供了一个刚性检测的能力；如果有，那么刚性检测被启用.

再论步长控制

当考虑轻度刚性问题时，有理由来考查标准积分步控制器（1）的某些替代.

该系统对一个化学反应建模：
这里基于 Dormand–Prince 系数定义了一个显式朗格-库塔方法，它不使用刚性检测：
这里求解该系统，并且使用功用函数 StepDataPlot 画出所用步长的图形：

应用标准步长控制器求解一个刚性或者轻度刚性问题会导致大振荡，有时会导致一些不良的步拒绝.

这一问题的研究，被称为步长控制稳定性.

它可以通过在一个嵌入式对中对高阶和低阶方法进行线性稳定性区域匹配来研究.

解决振荡的一个办法是推导特殊方法，但是这将使局部准确性打折扣.

PI 步长控制

积分步长控制（15）的一个令人感兴趣的替代是比例积分（Proportional-Integral）或者 PI 步长控制.

在这种情况下，步长是根据公式：

通过使用两个连续的积分步骤的局部误差来选取的，

它具有衰减的效果，因此，给出了一个更平滑的步长序列.

注意到积分步长控制（16）是（17）的一个特殊情况，并且在一个步骤被拒绝时采用：

选项 "StepSizeControlParameters"->{k1,k2} 可以用来指定 k1 和 k2 的值.

对第一个积分步骤为，(18) 中的尺度化误差估计采用 .

示例

刚性问题

定义一个类似于 IERK 的方法，使用选项 "StepSizeControlParameters" 来指明一个 PI 控制器.

这里，用户使用 Gustafsson 建议的通用控制参数：

以下指定步长控制参数：
再次求解该系统，可以看到步长序列现在要平滑的多：

非刚性问题

一般说来，I 步长控制器（19）能够对一个非刚性问题采取比 PI 步长控制器（20）更大的步长，如下面例子所示.

使用 I 步长控制器选择并求解一个非刚性系统：
使用 PI 步控制器，步长略小了一些：

由于这个原因，"StepSizeControlParameters" 的默认设置是 Automatic，它可以解释为：

微调

代替直接使用（23），通常的做法是使用安全因子，以确保误差在下一个步骤有很高的概率可以被接受，从而防止不必要的步骤拒绝.

选项 "StepSizeSafetyFactors"->{s1,s2} 指定在步长估计中使用的安全因子，这样（24）变成：

这里 s1 是一个绝对因子，而 s2 的大小通常随着方法的阶数改变.

选项 "StepSizeRatioBounds"->{srmin,srmax} 指定采取的下一个步长的边界，以满足：

选项总结

选项名
默认值
"Coefficients"EmbeddedExplicitRungeKuttaCoefficients指定显式朗格-库塔方法的系数
"DifferenceOrder"Automatic指定局部准确度的阶数
"EmbeddedDifferenceOrder"Automatic指定在一对显式朗格-库塔方法中嵌入的方法的阶数
"StepSizeControlParameters"Automatic指定 PI 步长控制参数（见（25））
"StepSizeRatioBounds"{,4}指定在新的步长中一个相对改变的界限（见（26））
"StepSizeSafetyFactors"Automatic指定在步长估计中使用的安全因子 （见（27））
"StiffnessTest"Automatic指定是否采用刚性检测功能

方法 "ExplicitRungeKutta" 的选项.

选项 "DifferenceOrder" 的默认设置 Automatic 基于问题、初值和局部误差容差选择默认系数阶数，以达到每个系数集合的方法的工作的平衡.

选项 "EmbeddedDifferenceOrder" 的默认设置 Automatic 指明嵌入式方法的默认阶数比方法阶数低一级. 这取决于 "DifferenceOrder" 选项的值.

选项 "StepSizeControlParameters" 的默认设置 Automatic 在刚性检测处于激活状态下使用值 {1,0}，否则使用 {3/10,2/5}.

选项 "StepSizeSafetyFactors" 的默认设置 Automatic 在采用 I 步长控制器时使用值 {17/20,9/10}，在采用 PI 步长控制器（28）时使用值 {9/10,9/10}. 使用的步控制器取决于选项 "StepSizeControlParameters" 和 "StiffnessTest" 的值.

选项 "StiffnessTest" 的默认设置 Automatic 将启动刚性测试，如果系数具有形式（29）.