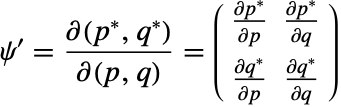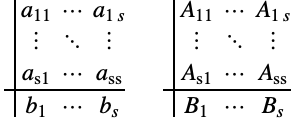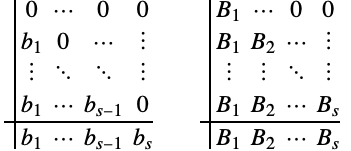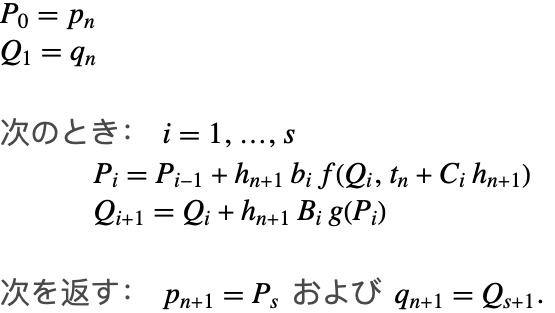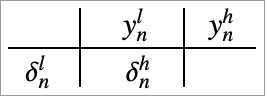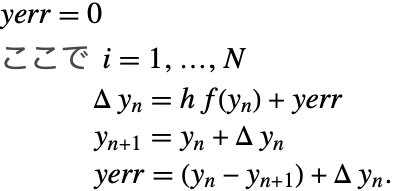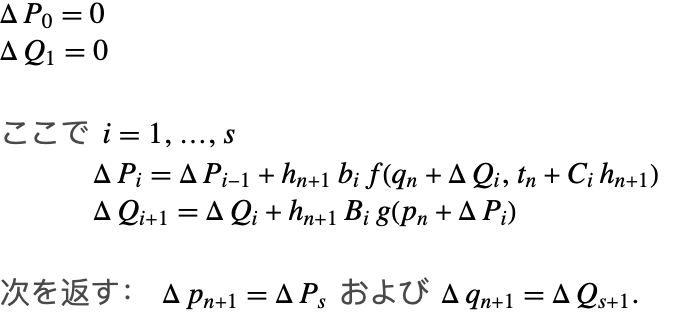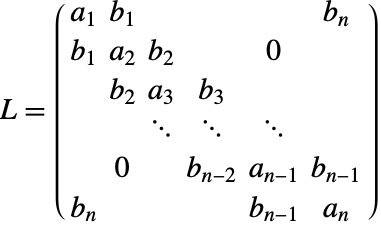NDSolveの"SymplecticPartitionedRungeKutta"メソッド

はじめに利用可能なメソッド
ハミルトン系自動次数選択
丸め誤差の軽減オプションの要約
例題

はじめに

ハミルトン力学系を数値的に解くとき，数値法によりシンプレクティックマップが生成されると便利である．

ハミルトン系

以下の微分方程式を例に取ってみる．

自由度 のハミルトン系は のときの(1)の特殊例である．ここで，以下が成り立つ．

は勾配演算子を表す．

は交代行列である．

ここで とはそれぞれ単位行列，× の零行列である．

の要素は，位置または座標変数と呼ばれ， の要素は運動量と呼ばれることが多い．

が自律であれば，である． は系の解すべてに一定である保存量である．応用すると，これは通常エネルギー保存に相当する．

ハミルトン系に適用された数値法(2)がシンプレクティックマップを生成する場合，この数値法はシンプレクティックであると言う．つまり，を領域で定義された 変換とする．

変換のヤコビアンは以下のようになる．

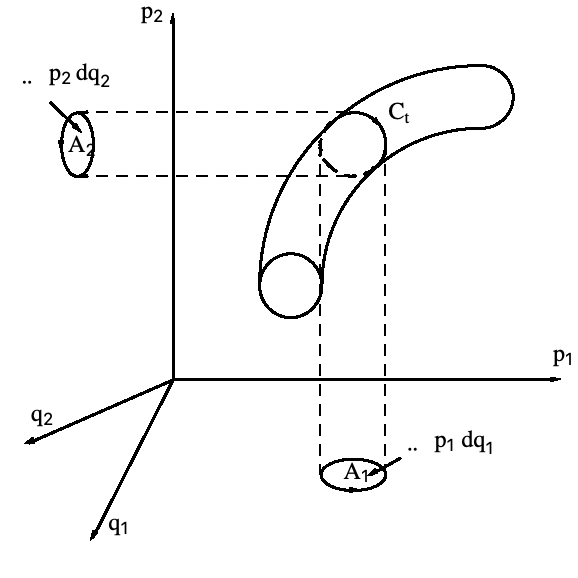
ハミルトン系の流れは，正準共役な座標と運動量をペアにして形成された平面上への投影と共に以下に描かれている．対象面積の合計は，流れが時間につれて発展しても一定である．

分割ルンゲ・クッタ(Runge–Kutta)法

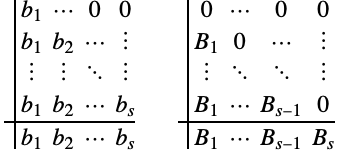
(3)のある要素を1つのルンゲ・クッタ法を使って積分し，別の要素を別のルンゲ・クッタ法を使って積分することが可能な場合がある． 段階法を全般に分割ルンゲ・クッタ法と呼び，自由パラメータは2つのButcher表で表される．

シンプレクティック分割ルンゲ・クッタ法

一般的なハミルトン系では，シンプレクティックルンゲ・クッタ法は必ず陰的である．

しかし分離可能なハミルトニアン では，シンプレクティック分割ルンゲ・クッタ法という陽的方法が存在する．

自由パラメータは(4)の代りに，

あるいは

のいずれかの形式を取る．(5)の 自由パラメータは簡略表記を使って表されることがある．

分離可能なハミルトン系の微分方程式系は以下のように書くことができる．

一般に，力評価 は計算量的に優勢である．緻密な出力が必要なときは，時間刻み毎に1つの力評価を保存することが可能なので，(6)よりも(7)の方が好まれる．

標準アルゴリズム

(8)の構造により，特に簡単な実装が可能である（[SC94]の例を参照のこと）．

アルゴリズム 1（標準 SPRK）

時間と重みは で与えられる．

ならば，アルゴリズム1はFirst Same As Last (FSAL)特性を持つので，実際には 段階法に簡約される．

例題

便利なパッケージをいくつかロードする：

調和振動

調和振動は，ばねに付けられた質点をモデル化する簡単なハミルトニアンの問題である．簡単にするために，単位質量とばね定数について考える．ハミルトニアンは，これらに対して分離可能な形式で与えられている，

運動方程式は以下によって与えられる．

入力

前進オイラー法

前進オイラー法を使って，調和振動の運動方程式を数値的に積分する：
このメソッドは散逸的であるため，軌道は原点の固定点に向かってあるいは，固定点から外に向かって螺旋を描く：
散逸的なメソッドは，通常ハミルトニアンの値の線形誤差を増長させる：

シンプレクティック法

シンプレクティック分割ルンゲ・クッタ法を使って，調和振動の運動方程式を数値的に積分する：
解は閉じた曲線となる：
散逸的なメソッドとは対照的に，シンプレクティック積分法でハミルトニアンに生じる誤差は有界のままである：

丸め誤差の軽減

シンプテクティック格子法というものが存在し，段階毎の丸めの累積を避けることができる場合があるが，このアプローチは常に可能であるわけではない[ET92]．

既出の例を取り上げる．ここでは刻み幅とメソッドの次数との組合せが，ハミルトニアンのエラーがIEEE倍精度演算で丸め単位の次数付近となるように選ばれている：

ハミルトニアンの誤差に面白い流れが見られるが，これは実際には，浮動小数点計算の数値的影響によるものである．

この現象は長時間の積分に影響を及ぼすことがある．

このセクションでは，このような誤差の影響を軽減するために，"SymplecticPartitionedRungeKutta"で使う公式を説明する．

流れを数値的に積分する場合，流れに沿ったものと流れに反したものの2種類の誤差がある．散逸系とは対照的に，流れに反したハミルトン系の丸め誤差は漸近的に劣化することがない．

常微分方程式の数値法の多くには，以下の形式の計算が含まれる．

ここで増分 の大きさは通常近似 よりも小さい．

が指数を表し，（ここで）が精度 ，基数 の演算 における数 の仮数を表すとする．

この場合，

および

と書くことができる．指数に従って整理すると，この量は以下のように表すことができる．

ここで左辺の数は右辺の数よりも小さい尺度となっている．

の指数と の指数に差があるために捨てられる 桁の基底を実質的に表す量 を効率よく計算する方法はどのようなものであろうか．

補正加算

補正加算が基本的に意図するのは， ビットの演算だけを使って ビットの加算をシミュレートすることである．

例題

以下は，初期値に固定量を繰返し加えてゆく．累積丸め誤差が，結果に大きな影響を及ぼす：

増分はアプリケーションによりさまざまで，操作の数は事前には分かっていない．

アルゴリズム

補正加算（例として[B87]と[H96]を参照のこと）は，式

が，以下のアルゴリズムで置き換えられるように，和とともに丸め誤差を計算する．

アルゴリズム 2（補正加算）

このアルゴリズムは，ベクトルの成分全体で実行される．

例題

関数CompensatedPlus（Developer`コンテキスト）は，補正加算のアルゴリズムを実装する．

1つの和から次の和へと，丸め誤差を繰返しフィードバックすると，丸め誤差の影響が著しく軽減される：

CompensatedSummationはドキュメントされていないオプションであるが，これはNDSolveの組込み積分法で補正加算を使うかどうかを制御するものである．

別のアルゴリズム

補正加算の用途はいろいろある．

そのひとつに，アルゴリズム1のメインループでの各加算の更新における誤差を計算するというものがある．

ここで別のアルゴリズムを下に挙げる．これは演算コストが減少されており，より一般的な応用が効くため提唱するするものである．必要な構成要素は増分 と である．

アルゴリズム 3（増分SPRK）

要求される値 と は，補正加算を使って得る．

補正加算は，アルゴリズム3のメインループでの各加算の更新でも使用することができる．しかし，実験の結果，正確さの向上は比較的小さいのに，無視できないほどの間接費がかかることが分かった．

数値例題

丸め誤差モデル

調和振動(9)のハミルトニアンの相対誤差において想定される丸め誤差は，数量化されるようになった．確率的平均解析が，最悪上限に優先して考慮される．

等しい偏差確率の一次元ランダムウォークでは， ステップ後に想定される絶対距離は である．

直近へのIEEEの丸めを使った浮動小数点操作，，， の相対誤差は，以下の上限を満足する[K93]．

使用したマシンの浮動小数点数を表すのに基底 が使われ，IEEE倍精度には が使われている．

従って， ステップ後の丸め誤差は，任意の定数 について，ほぼ

のようになることが予想される．

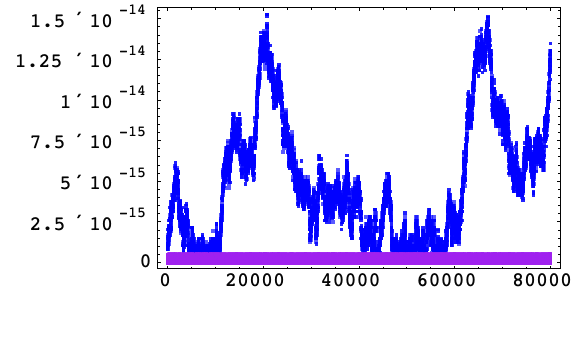
次の例では固定刻み幅1/25が使われ，積分は区間[0, 80000]で合計の積分ステップで実行されている．ハミルトニアンの誤差は200積分ステップ毎に抽出される．

Yoshidaの八次15段階の(FSAL)メソッドDを使う．Yoshidaの六次七段階(FSAL)メソッドAで同じ積分ステップ数と刻み幅1/160を使っても，同様の結果が得られる．

補正加算なし

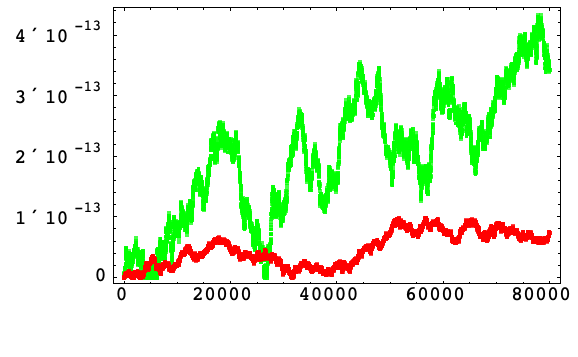
以下は，アルゴリズム1の標準公式でのハミルトニアンの相対誤差（緑）および調和振動(10)のアルゴリズム3の増分公式でのハミルトニアンの相対誤差（赤）である．

15段階法でのアルゴリズム1は となる．

増分アルゴリズム3では，内部段階は刻み幅の次数すべてであり，重大な丸め誤差だけが各積分ステップの最後で起っている．よって は観察される向上性と十分一致している．

このことは，アルゴリズム3では十分小さい刻み幅を使うと，丸め誤差の増大はメソッドの段階数に依存しないということを示している．これは特に高次で有利である．

補正加算あり

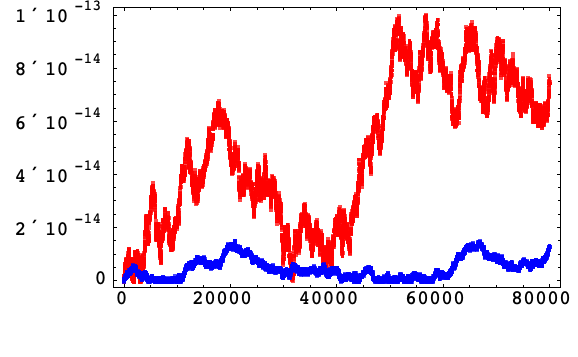
以下は，調和振動(11)のアルゴリズム3の増分公式でのハミルトニアンの相対誤差で，補正加算なしの場合（赤）と，補正加算付きの場合（青）である．

アルゴリズム3で補正加算を使うと，誤差の増大は刻み幅に比例した因数によって簡約されるように，偏差 のランダムウォークを満足しているように見える．

任意精度

以下は，調和振動(12)のアルゴリズム3の増分公式でのハミルトニアンの相対誤差で，IEEE倍精度演算を使った補正加算付きの場合（青）と，32桁のソフトウェア演算の場合（紫）である．

しかし，ソフトウェア演算を使って得る結果は，機械演算より1桁近く遅いので，丸め誤差効果を軽減する価値がある．

例題

静電波

以下は摂動する の静電波をモデル化する非自律のハミルトニアン（時間依存ポテンシャルを持つ）である．各静電波は同じ波数と振幅を持つが，時間周波数 は異なる（[CR91]を参照のこと）．

以下は周波数 ，, を持ち，次元が のハミルトニアン(13)の微分方程式系を定義する：

ポアンカレ断面の一般的な計算方法は「微分方程式のイベントと不連続性」に記載されている．変数の空リストを指定すると，数値積分のデータをすべて保存しなくてもよくなる．

積分は比較的多数のステップ数でシンプレクティック法を使って実行される．解は，時間が の倍数になったところでSowおよびReapを使って収集される：
時間の間隔が での解を表示する：
比較のため，同じ次数の陽的ルンゲ・クッタ法を使って，ポアンカレ断面を計算する：
この方法では，細かい構造詳細の解像度があまりよくない：

戸田格子

戸田格子は，ペアの指数エネルギーと相互作用を及ぼしあう線上の粒子をモデル化し，ハミルトニアンによって支配される．

周期境界条件 が強制される場合を考えてみる．

戸田格子は等スペクトルの流れの例である．以下の表記

を使うと，以下の行列の固有値はその流れの保存量になる．

のときの戸田格子問題の入力を定義する：
数の行列の固有値を計算して昇順に保存するような関数を定義する．これで固有値を記号的に計算することが避けられる：
"ExplicitMidpoint"メソッドを使って戸田格子方程式を積分する：

固有値の絶対誤差が，積分区間全体でプロットされるようになった．

NumberEigenvaluesの結果の次元（結果は明示的なリストではないため）を指定し，InvariantErrorFunctionを使って指定する絶対誤差が誤差の符号（デフォルトではAbs）を含むよう指定するために，オプションを使う．

固有値は，"ExplicitMidpoint"メソッドでは明確に保存されない：
"SymplecticPartitionedRungeKutta"メソッドを使って戸田格子方程式を積分する：
固有値の誤差が，積分全体で有界のままになった：

等スペクトルの流れの数値メソッドについての近年の研究は，[CIZ97]，[CIZ99]，[DLP98a]，[DLP98b]に記述されている．

利用可能なメソッド

デフォルトメソッド

以下の表は，SPRKの現在のデフォルトのリストである．

陽的ルンゲ・クッタ法の場合と異なり，文献では高次のSPRK法の係数は数値的にしか与えられていない．例えば，Yoshida[Y90]は14桁精度に等しい精度の係数だけを与えている．

NDSolveは任意精度でも使用できるので，ソルバで使われるのと同じ精度の係数を得るための処理が必要である．

係数の閉形式が使えないときは，対称合成の係数の次数方程式は，FindRootを使い既知の機械精度解から始めて任意精度で調整できる．

代替メソッド

新しいNDSolveフレームワークのモジュラ設計により，代替メソッドを追加し，デフォルトメソッドの代りにそれを使うことが簡単になった．

積分を実行する前に以下のようなチェックを行う．

例題

摂動ケプラー問題を選ぶ：
ForestとRuth[FR90]，CandyとRozmus[CR91]，Yoshida[Y90]の四次メソッドの係数の数値近似を計算する関数を定義する：
これは係数の機械精度近似である：
これはYoshidaの係数を使って，シンプレクティック分割ルンゲ・クッタソルバを実行する：
位置変数（座標）の解をハミルトン公式でプロットする：

自動次数選択

異なる次数のさまざまなメソッドが使用できるとすると，自動的に適切なメソッドを選ぶ方法があると便利である．このために，各メソッドについてある程度の作業が必要になる．

SPRKメソッドでは，段階数 （メソッドがFSALの場合は ）だけの操作が必要である．

定義 （単位ステップあたりの作業量）

次のメソッドのひとつの積分ステップの刻み幅を ，作業推定を とすると，単位ステップあたりの作業量は で与えられる．

がメソッドの次数の非空集合を， がの第 要素を，が濃度（要素数）を表すものとする．

デフォルトのSPRKメソッドの作業量を比較すると，となる．

前提条件となるのは， 次の数値法の初期刻み幅 の推定である（[GSB87]と[HNW93]を参照）．

最初に考えらなければならないことは，初期刻み幅推定 が自由に選べるときのことである．以下のアルゴリズムは，低次からブートストラップすることにより，単位ステップあたりの作業量を局所的に最小化する次数を見付ける．

アルゴリズム 4（ は自由）

次に考慮しなければならないことは，初期刻み幅推定 h が与えられているときのことである．下のアルゴリズムは，指定された絶対・相対局所許容誤差を満足する一方で，計算コストを最小化するメソッドの次数を与える．

アルゴリズム 5（ が指定されている）

シンプレクティック積分では固定値が含まれることが多いが，アルゴリズム4と5は，最適な刻み幅と次数が積分過程で変化する可能性があるので，ヒューリスティックといえる．それでもどちらのアルゴリズムも悪い選択をしないよう，局所許容誤差，系の次元，初期条件等の重要な積分情報を含んでいる．

例題

距離の2乗に反比例したエネルギーで，原点に向かう平面上の質点の運動を描くケプラー問題を考える．

初期条件として，離心率 で

を取る．

アルゴリズム 4

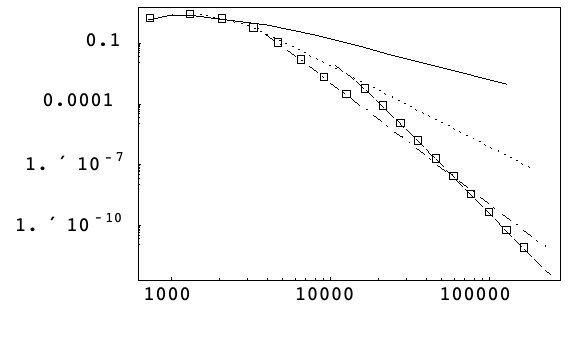
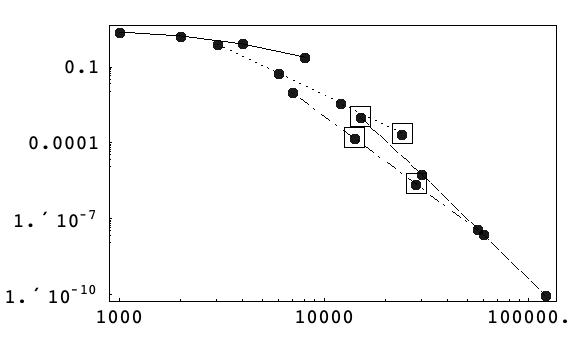
以下の図は，アルゴリズム4に従って，さまざまな許容誤差で自動的に選ばれたケプラー問題(14)のメソッドを，最大絶対位相誤差と作業量の両対数スケール上に示している．

このアルゴリズムは，必要時期よりもわずかに早く八次メソッドに切り換えているが，最適なメソッド付近に停滞するという妥当な結果を示している．

これは初期刻み幅ルーチンが低次の導関数推定に基づいており，高次メソッドの選択には理想的ではないということで説明できる．

アルゴリズム 5

次の図は，アルゴリズム5に従って，絶対局所許容誤差10-9，刻み幅1/16，1/32，1/64，1/128で自動的に選ばれたケプラー問題(15)のメソッドを，最大絶対位相誤差と作業量の両対数スケール上に示している．

局所許容誤差と刻み幅が固定されると，コードはメソッドの次数しか選べない．

刻み幅が大きいと高次のメソッドが，小さいと低次のメソッドが選ばれる．どちらの場合も，選ばれたメソッドは指定された許容誤差を得るための作業量を最小化する．

オプションの要約

オプション名
デフォルト値
"Coefficients""SymplecticPartitionedRungeKuttaCoefficients"シンプレクティック分割ルンゲ・クッタの係数を指定する
"DifferenceOrder"Automaticメソッドの局所精度の次数を指定する
"PositionVariables"{}ハミルトン公式の位置変数のリストを指定する

SymplecticPartitionedRungeKuttaメソッドのオプション