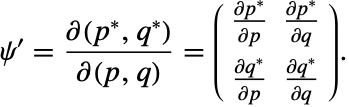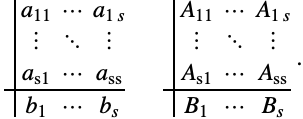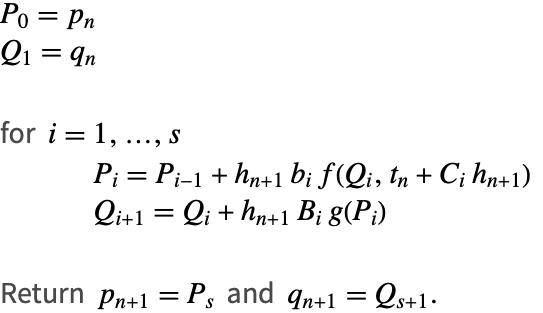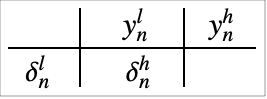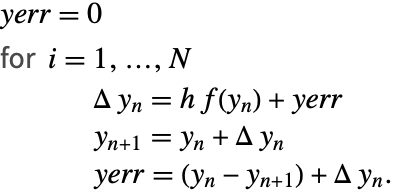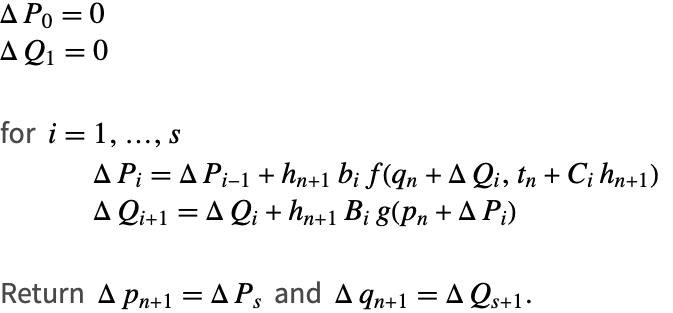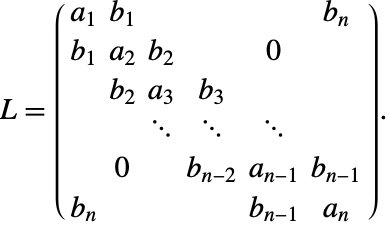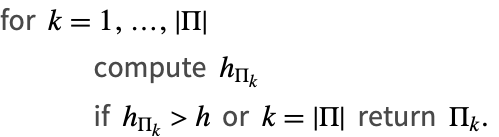NDSolve 的 "SymplecticPartitionedRungeKutta" 方法

引言可用方法
哈密顿系统自动阶数选择
减少舍入误差选项总结
示例

引言

当数值求解哈密顿动力系统时，如果数值方法产生一个辛映射，则是有利的.

哈密顿系统

考虑一个微分方程

一个自由度数为 的哈密顿系统是 (1) 的特例，其中 ，满足

这里 表示梯度算子：

而 是斜对称矩阵：

其中 和 分别是 × 的单位矩阵和零矩阵.

分量常常被称为位置或者坐标变量，而 分量则被称为动量.

如果 是自治的（autonomous），. 那么 是一个随系统的求解保持不变的守恒量. 在应用中，这通常相应于能量守恒.

一种应用于哈密顿系统 (2) 的数值方法被认为是辛的（symplectic)，如果它产生辛映射（symplectic map）. 即，令 是定义在域 上的一个 变换：

其中该变换的雅可比为：

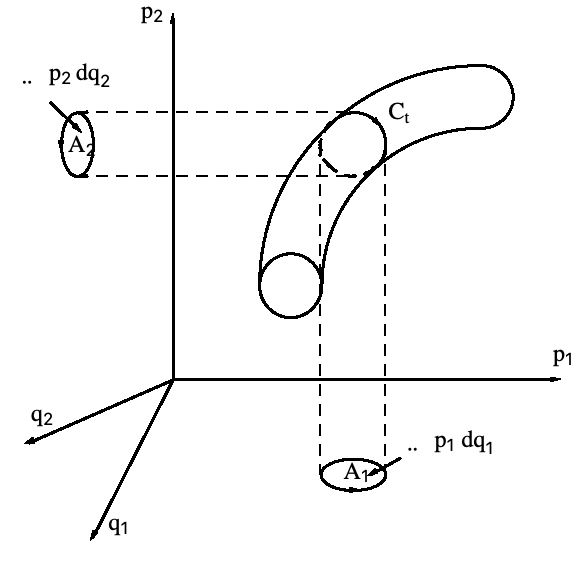
一个哈密顿系统的流，是同其在正则共轭坐标和动量对形成的平面上的投影一起来描述的. 当流随着时间演变时，有向面积的和保持不变.

分区朗格-库塔方法（Partitioned Runge–Kutta Method）

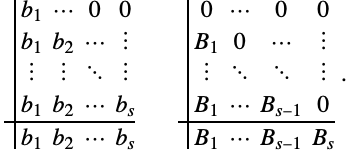
有时候，可以对 (3) 的某些分量使用朗格-库塔方法积分，对其他分量，则使用一个不同的朗格-库塔方法积分. 总的 -级方案被称为分区朗格-库塔方法，而自由参数则用两个 Butcher 表（Butcher tableaux） 表示：

辛分区朗格-库塔（SPRK）方法

对于一般哈密顿系统，辛朗格-库塔方法必然是隐式的.

然而，对于可分离哈密顿 则存在对应于辛分区朗格-库塔方法的显式方案.

与 (4)不同，自由参数现在可以要么采用如下形式：

或者如下形式：

(5) 的 个自由参数有时候用简写形式 表示.

一个可分离哈密顿系统的微分系统可以写为：

一般来说，力的计算 在计算上是主导的，因而 (6) 比 (7) 更可取，因为当稠密输出为必需的时候，有可能可以在每个时间步骤上节省一个力的计算.

标准算法

(8) 的结构允许采用一个特别简单的实现方法（例如，见 [SC94]）.

算法 1 （标准 SPRK）

时间权重由 给出.

如果 ，那么算法1 实际上被简化为一个 阶段方案，因为它具有最先与最后相同（ First Same As Last 即FSAL）的属性.

示例

这里加载一些有用的程序包：

谐振子

谐振子是一个模拟将一个质点系在弹簧上的简单的哈密顿问题. 为了简单起见，考虑单位质量和弹簧常数，此时哈密顿量如下可分的形式给出：

运动方程为：

输入

显式欧拉方法

使用显式欧拉方法，对谐振子的运动方程进行数值积分：
由于该方法是耗散的，弹道轨迹从原点处的固定点螺旋进入或者离开：
耗散方法通常对于哈密顿量的值呈线性误差增长：

辛算法

使用辛分区朗格-库塔方法，对谐振子的运动方程进行数值积分：
该解现在是一个闭合曲线：
与耗散方法相反，辛积分器产生的哈密顿量的误差是保持有界的：

减少舍入误差

在某些情况下，存在有格点辛方法，可以避免一步一步的舍入误差累积，但是这种方法并不总是可能的 [ET92].

考虑前面的例子，其中方法的步长和阶数的组合的选择使得哈密顿量的误差大约在 IEEE 双精度算术上的单位舍入误差的量级上：

在哈密顿上的误差有一个奇怪的浮动，这其实是一个浮点运算的数值产物.

这种现象可以对长时间积分产生影响.

本节描述了 "SymplecticPartitionedRungeKutta" 所使用的表述，以减少这种误差的影响.

在对一个流进行数值积分时，有两种误差类型，即沿着流的误差 (along the flow) 和垂直于流的误差 (transverse to the flow). 与耗散系统相反，哈密顿系统上垂直于流的舍入误差不会渐近衰减.

许多常微分方程的数值方法包含如下形式的计算：

其中，增量 在大小上通常比近似值 更小.

对精度为 底数为 的算术上的数 ，令 表示其的指数，而 ，，为尾数：.

那么，您可以写出：

以及

将指数对齐，那么这些数量可以形象地表示为：

其中，左边的数具有一个比右边的数更小的量级.

我们感兴趣的是寻找一个有效方法来计算 ，它实际上表示由于 和 指数的差异而被略掉的底数 数位.

补偿总和 （Compensated Summation）

补偿总和的基本动机是仅使用 （二进制）位算术，模拟 （二进制）位加法运算.

示例

这里重复对一个初始值增加一个固定的数量. 累积舍入误差对结果会产生显著的影响：

在许多应用中，增量可能会有所不同，而运算的次数事先并不知道.

算法

补偿总和（例如见 [B87] 和 [H96]）随着求和计算舍入误差，使得

被替换为：

算法 2（补偿总和）

对于向量，该算法对各分量分别计算.

示例

函数 CompensatedPlus（在 Developer` 中）执行补偿总和算法.

通过不断从一个和回馈舍入误差到下一个和，舍入误差的影响被大大降低了：

一个未公开的选项 CompensatedSummation 控制 NDSolve 中的内置积分算法是否采用补偿总和.

另一种算法

补偿总和可以采用各种不同的方式.

一种方法是在算法1中主循环的每次加法更新中计算误差.

下面要给出另一种算法，因为它有更广泛的适用性，而且算术成本低. 其基本要素是增量 和.

算法 3 （增量 SPRK）

所需值 和 通过使用补偿总和获得.

补偿总和也可以用于算法3的主循环总的每次加法更新中，但是我们的实验表明，这会增加一个不可忽视的开销，而准确度上的提高却相对较小.

数值演示

舍入误差模型

在这里，谐振子 (9) 的哈密顿量的相对误差中预期舍入误差将被量化. 概率平均情况分析 (A probabilistic average case analysis) 比一个最坏情况上限 (a worst case upper bound) 优先考虑.

对于一个具有等概率偏差的一维随机游动，经过 步后的预期绝对距离为 .

使用 IEEE 最近舍入模式，浮点运算 、、、 的相对误差满足下面界限 [K93]:

其中，基 用于表示机器上的浮点数，而对于 IEEE 双精度数，.

因此，对于某一常量 ， 步后的舍入误差预计约为：

在下面的例子中，我们采用大小为 1/25 的固定步长，而且在区间 [0, 80000] 上一共使用 积分步执行积分. 哈密顿量的误差在每隔 200 积分步上被采样.

我们采用 Yoshida 的第 8 阶 15-阶段 (FSAL) 方法 D. 对于 Yoshida 的第 6 阶 7-阶段 (FSAL) 方法，使用相同的积分步骤以及大小为 1/160 的步长，可以获得相似的结果.

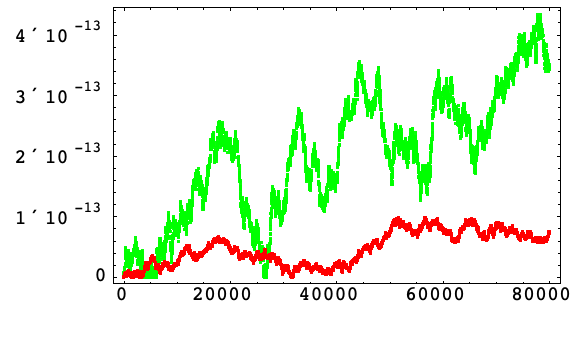
不使用补偿求和

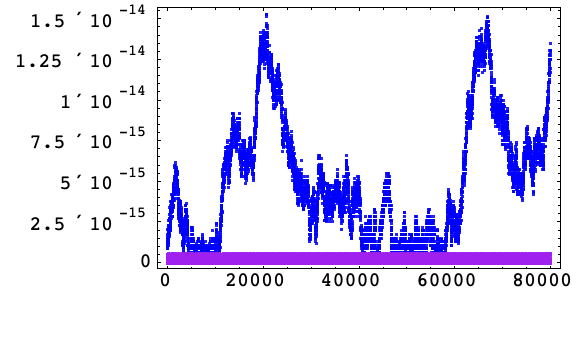
这里是谐振子 (10) 的哈密顿量的相对误差的图示，绿色为算法 1 中的标准形式，红色为算法 3 的增量形式.

对于一个 15-阶段方法，算法 1 对应于 .

在增量算法 3 中，内部阶段都具有步长的量级，而仅有的显著舍入误差出现在每个积分步骤的末尾；因此，，这与观察到的改善良好地吻合.

这表明了对于算法 3，使用足够小的步长时，舍入误差的增加与方法的阶段数目无关，而这对于高阶问题来说特别有利.

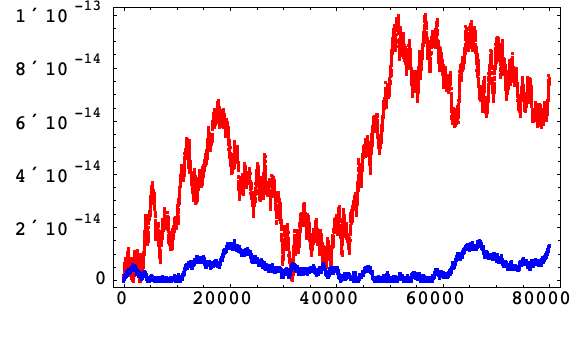
使用补偿总和

这里显示谐振子 (1) 哈密顿量的相对误差，以展示算法 3 中不使用补偿总和（红色）和使用补偿总和（蓝色）的增量形式.

对算法 3 使用补偿总和，误差增长呈现为满足偏差为 的一个随机游动，因此它减少了一个与步长成正比的因子.

任意精度

下面显示的是使用补偿总和的算法 3 中的增量形式在使用IEEE双精度算术（蓝色）和 32 位十进制软件算术（紫色）时，谐振子 (1) 哈密顿量的相对误差.

但是，使用软件算术获得解要比使用机器算术大约慢一个数量级，因此采用减少舍入误差影响的策略是有值得的.

示例

静电波

下面是一个模拟 个扰动静电波的非自治哈密顿（它有一个与时间有关的势能），每个静电波都具有相同的波数和振幅，但是有不同的频率 （见 [CR91]）.

这里从哈密顿（1）定义了一个微分系统，维数为 ，频率为 、、：

"微分方程中的事件和不连续性" 中有对计算彭加莱截面 （Poincaré section）的一般技术的描述. 对变量指定一个空列表避免了存储数值积分的所有数据.

积分是使用辛方法在相对大的步骤数目中执行的，解是使用 Sow 和 Reap 在时间是 的倍数时收集的：
这里在时间区间 中显示解：
作为对比，使用相同阶数的显式朗格-库塔方法，计算一个彭加莱截面：
使用该方法，精细结构细节以一个较不满意的方式明确求解：

Toda Lattice

Toda lattice 模拟在一条线上，两两之间具有指数型相互作用的粒子. 其哈密顿量为：

考虑满足周期边界条件 的情况.

Toda lattice 是一个等谱流的例子. 使用记号

那么下面矩阵的特征值是流的守恒量：

定义 的 Toda lattice 问题的输入：
定义一个函数来计算数字组成的矩阵的特征值，按升序排序. 这避免了符号式计算特征值：
使用 "ExplicitMidpoint" 方法，对 Toda lattice 的方程积分：

现在在积分区间上绘制在特征值上的绝对误差的图形.

使用选项来指明 NumberEigenvalues 的结果的维度（因为它不是一个显式列表），而使用InvariantErrorFunction 指定的绝对误差应该包括误差的符号（默认时用 Abs）.

很明显，应用 "ExplicitMidpoint" 方法，特征值并没有守恒：
使用 "SymplecticPartitionedRungeKutta" 方法，对 Toda lattice 方程积分：
在特征值上的误差现在在整个积分中保持有界：

等谱流的一些在数值方法上的近期的工作可以参阅 [CIZ97]、[CIZ99]、[DLP98a] 和 [DLP98b].

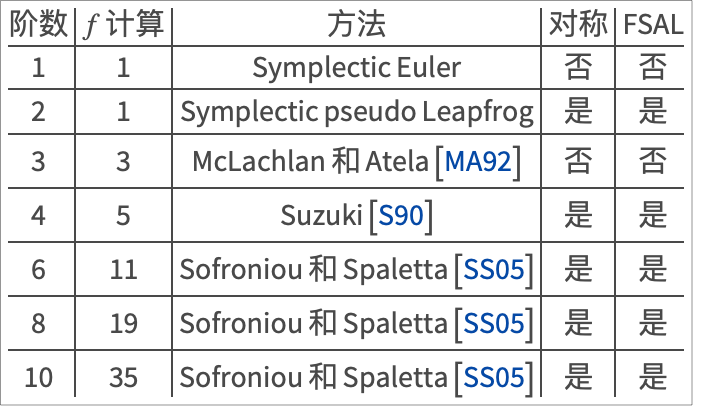
可用方法

默认方法

下面的表格列出目前 SPRK 方法的默认选择.

与显式朗格-库塔方法的情况不同，在文献中，高阶 SPRK 方法的系数只以数值形式给出. 例如，Yoshida [Y90] 只给出精确到14十进制数位的系数.

由于 NDSolve 对任意精度适用，用户需要一个工序来获得与在求解器中使用的精度相同的系数.

当没有系数的闭式时，对称组合系数的阶数方程可以使用 FindRoot ，从已知的机器精度解上开始，在任意精度上精化.

其它方法

由于新的 NDSolve 框架的模块设计，可以很便捷地增加一个其他的方法并且使用它，而不是用默认方法之一.

在任何积分执行之前，要进行一些检查：

实例

选择扰动开普勒问题：
定义一个函数，来计算 Forest 和 Ruth [FR90]、Candy 和 Rozmus [CR91] 以及 Yoshida [Y90] 的四阶方法的系数的数值近似：
下面是系数的机器精度近似：
这里调用使用 Yoshida 系数的辛分区朗格-库塔求解器：
这里画出在哈密顿形式中的位置变量（或者坐标）的解：

自动阶数选择

鉴于目前有各种各样不同阶数的方法可供使用，拥有自动选择一个合适的方法的手段是非常有用的. 为了做到这一点，我们需要有对每种方法的性能的一个衡量.

对于一个SPRK方法性能的一个可行的衡量是阶段数目 （或者是 ，如果该方法是 FSAL 的话）.

定义 （每个单位步骤的工作量）

给定一个步长 和对一个阶数为 的方法的一个积分步骤的工作估计 ，每个单位步骤的工作量由下式给出： .

令 表示方法阶数的一个非空集合， 表示 的第 个元素，而 表示基数（元素数目）.

默认SPRK方法的工作比较给出了 .

一个先决条件是估计阶数为 的数值方法的初始步骤 的一个程序（例如，见 [GSB87] 或者 [HNW93]）.

第一种要考虑的情况是初始步骤估计 可以自由选择. 通过从低阶开始引导，下面的算法寻找局部最小化每个单位步骤工作量的阶数.

算法 4 （ 任意）

要考虑的第二种情况是当初始步骤估计 h 给定的时候. 那么，下面算法给出了最小化计算代价的方法阶数，同时满足给定的绝对和相对局部误差容差.

算法 5 （指定 ）

算法 4 和 5 是探索式的，因为最优步长和阶数可能会在积分过程中改变，虽然辛积分往往包含有固定的选择. 尽管如此，这两种算法都综合了积分的突出信息，如局部误差容差，系统维度，和初始条件，以避免不当的选择.

实例

考虑开普勒问题，它描述一个质点，在来自原点与距离的平方成反比的吸引力作用下，在位形平面内的运动：

初始条件采用

其中，偏心率 .

算法 4

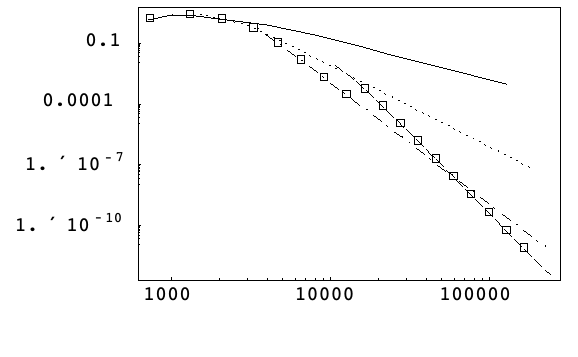
下面在最大绝对相误差相对工作量的log-log图上，显示对于开普勒问题（1），根据算法4，在不同的容差上，自动选择的方法.

可以看出，算法在保持最优方法方面表现良好，虽然它有点过早早切换到第 8 阶方法.

这可以通过如下事实解释：起始步长例程是以低阶导数估计为基础的，而这对于选择高阶方法来说，可能并不理想.

算法 5

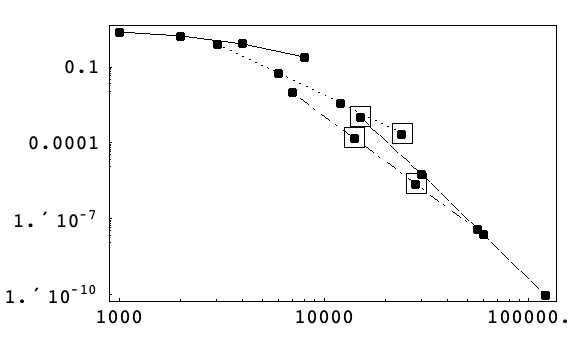
下面在最大绝对相误差相对工作量的log-log图上，显示对于开普勒问题（1），根据算法5，使用绝对局部误差容差 10-9，和步长 1/16、1/32、1/64、1/128 时，自动选择的方法.

在局部容差和步长固定的情况下，代码只能够选择方法的阶数.

对于较大的步长，则选择高阶方法，而对于较小的步长，则选择低阶方法. 在每种情况下，方法的选择都使工作量最小化，以满足给定的容差.

选项总结

选项名
默认值
"Coefficients""SymplecticPartitionedRungeKuttaCoefficients"指定辛分区朗格-库塔方法的系数
"DifferenceOrder"Automatic指定方法的局部准确度的阶数
"PositionVariables"{}指定哈密顿表述中位置变量的一个列表

方法 "SymplecticPartitionedRungeKutta" 的选项.