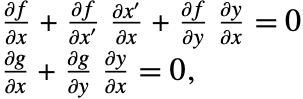微分代数方程的状态空间方法
如果雅克比矩阵 
和 
都是可逆的，那么根据隐式函数理论，系统可以使用状态空间格式表示为：
可逆要求等价于索引为1的系统，因此给予状态空间格式的方法对于微分代数方程的索引为1的系统是合适的. 最常见的格式 
和 
是恒等矩阵.
"StateSpace" 时间积分方法基于这个表示法. 给定 
的数值，牛顿迭代用于求 
和 
. 对于要求计算右侧函数的内在常微分方程方法，返回 
的数值. 在计算直接，保存前面计算得到的导数和代数变量的值来初始化下一步迭代的初始化迭代.
从状态空间格式得到的常微分方程经常相当严格，并且要求雅克比. 由于这可以通过使用有限微分计算，使用该问题结构更准确和有效，因为已经计算矩阵 
和 
. 右侧雅克比可以通过关于 
对划分系统求导求得
从牛顿迭代通常保存 
和 
的矩阵分解，因此可以有效计算逆矩阵的应用.
"StateSpace" 方法通常比默认的 "IDA" 多步方法更慢，因为相对于每个时间步骤，它必须对每个迭代求解（可能通过迭代的方式）
和 
，对于每个时间步骤可能有许多计算需要完成. 在某些情况下，存在一些可能的优势可以补偿该速度：对于函数计算是局部的迭代可能更加稳定，一个A 稳定的内在迭代方法可以用于改善整体稳定性，该方法是一种一步方法，当内在方法是一步，并且该方法的完成允许任意精度的解.
"StateSpace" 方法的 Method 选项帮助您选择内在的积分方法.
分块下三角（BLT）格式
取决于系统的结构，把系统排序成分块下三角（BLT）格式是有优势的. 使用 BLT 格式产生更多较小规模的子系统的解. 如果最大的分块尺寸可以显著减少，使用该结构可以显著降低牛顿迭代的计算复杂度.
BLT 格式用于求解微分代数方程的大量方法中，包括一致初始化，设置索引化简的虚拟导数以及求解系数线性系统. 这里的描述着重于它在状态空间方法中的使用，但是可用性也扩展到其他领域.
在最简单的格式中，BLT 排序是一种矩阵算法，并且是在 Wolfram 语言中访问它的最佳常见方式.
| SparseArray`BlockTriangularOrdering[s] | 给出矩阵 s 的行和列的排序 {{r1,…,rb},{c1,…,cb}}，以满足 s[[rk,ck]] 是重新排序后的矩阵 s[[r,c]] 的对角线上的第 k 分块，其中 r=Flatten[{r1,…,rb}] 和 c=Flatten[{c1,…,cb}]，而重新排序后的矩阵的所有其他元素都出现在对角线下方 |
当矩阵 s 是非奇异的情况下，沿着对角线往下计算，每个连续分块的变量只取决于前面分块的1. 这表示线性方程 
可以通过沿着对角线顺序求解，按顺序求解每个分块子系统，这样可能节省大量计算精力.
对于该系统，分块的尺寸都是1，这意味着它特别容易求解，因为您可以按顺序挑选变量值，正如在 BLT 排序中的方程列表中一样. 对于状态空间方法，给出 h={h1,h2,h3}，因此获取导数 h′ 是常见的.
正如前面，我们可以沿着对角线开始计算，按顺序求解每个子问题. 一旦求得 x'、y 和 yd1（非线性问题可以使用标量牛顿求解器完成），那么只有 3×3 方块需要被求解，以获得 x1'、yd2 和 λ.
注意，方程 
对 
存在两个解. 连续性通过使用前面的数值开始牛顿迭代保持.
可以引导状态空间方法来以各种方式使用分块下三角排序，使用方法选项 "BlockLowerTriangular".
"BlockLowerTriangular" 方法的选项设置.
对于这个例子，时间非常接近，因为系统很小. 对于在 BLT 在排序后雅克比中具有较小的分块的大型系统，差值可以更显著.