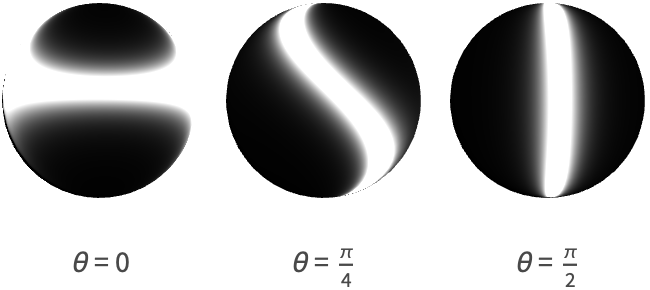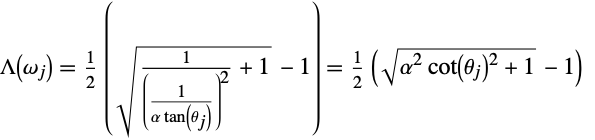Physically Based Rendering
| Motivation | The Reflectance Equation |
| Physical Correctness | Additional Effects |
| Introduction to Rendering | References |
Physically based rendering (PBR) is an approach to computer graphics that seeks to render images by modeling the behavior of light in the real world. PBR is an umbrella term that covers a variety of areas, such as physically based shading, cameras and lights.
Physically based shading (PBS) is a key component of PBR, and is implemented in the Wolfram Language as MaterialShading. The rest of this document will cover its implementation and the underlying theory behind it.
Motivation
Physically based rendering techniques are now commonplace in 3D graphics programs. They provide some key advantages over purely artistic techniques, including:
1. Physical accuracy — Since PBR techniques more closely resemble the behavior of real light, pipelines that utilize them are able to achieve more photorealistic renders.
2. Intuitive parameterization — Parameters in PBR shaders are based on physical properties instead of purely aesthetic values. This makes it easier to adjust the parameters to match real-world materials. It also becomes harder to create physically implausible materials.
3. Portability — Most modern graphics programs support PBR materials, and their implementations tend to be similar across different programs. Therefore, one can often copy the parameters of a material from one rendering program to another and achieve similar results.
Physical Correctness
Nearly all rendering implementations are somewhat physically based. What distinguishes the category of PBR techniques is that they adhere to a set of properties and laws. These include:
1. Conservation of energy — No surface can reflect more light than it receives.
2. Positivity — Surfaces cannot reflect a negative amount of light.
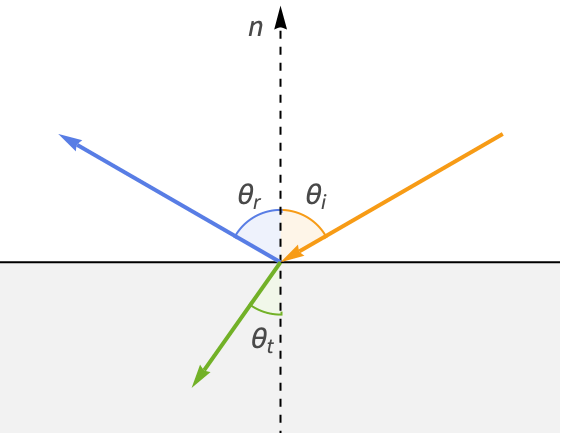
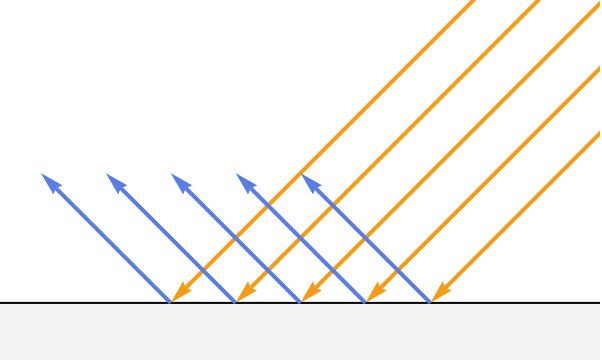
3. Law of reflection — The angle of incidence equals the angle of reflection for specular light.
4. Fresnel equations — Light reflects and refracts at the interface of media in accordance with the Fresnel equations.
5. Helmholtz reciprocity — Light rays behave identically when following the same path, regardless of their direction. This allows us to accurately "trace" light rays from the viewer back to their source.
The specific influence of these properties is discussed in more detail later in this document.
Limitations
PBR techniques simulate light using geometrical optics (also known as ray optics), which models light as individual rays. This model assumes light rays travel in straight-line paths, with the exception of reflecting or refracting at the interface of dissimilar media.
Due to this simplified model, some aspects of light are ignored, such as:
• Polarization — Polarized light can behave differently when hitting certain surfaces.
• Interference — Separate light waves can interact to cancel or magnify each other.
• Relativistic Doppler effect — Objects moving at high speeds can alter the frequency of light waves reflected off their surface.
• Gravitational lensing — The direction of light can be altered by gravity.
With that said, PBR techniques are still able to convincingly simulate a wide range of materials.
Introduction to Rendering
The central question of PBS is how to determine both the quantity and direction of light leaving the surface of an object. To understand the importance of this question, the rest of this section will explain how this information can be used to render a scene.
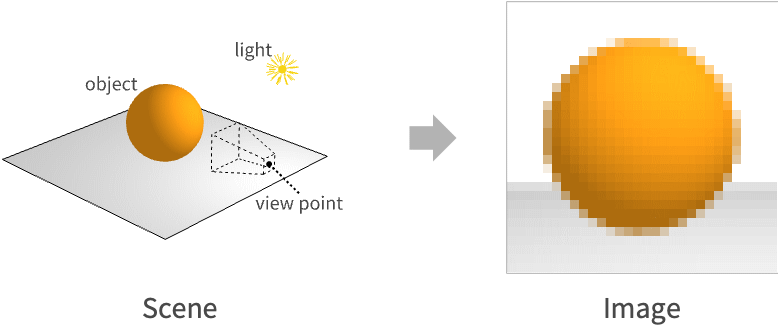
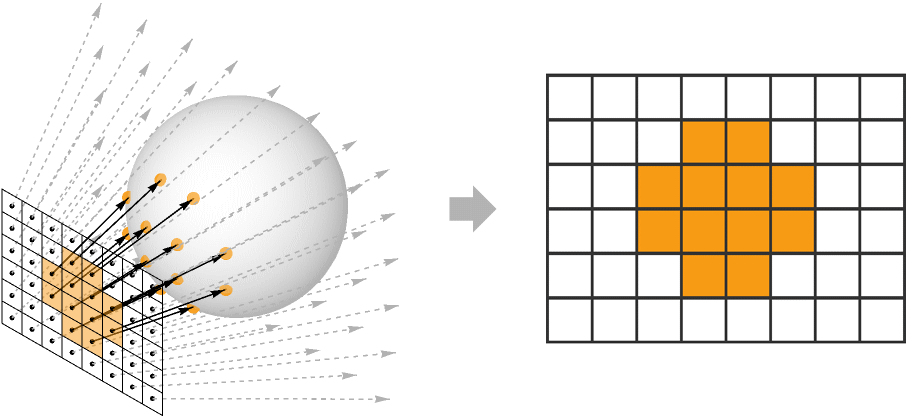
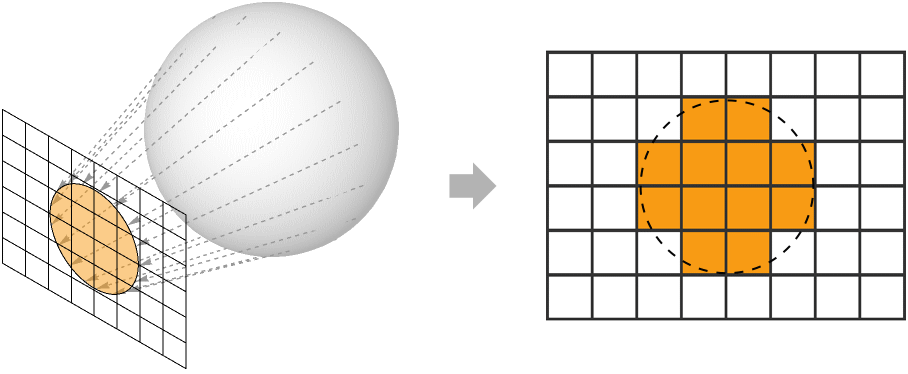
In 3D computer graphics, rendering is the process of converting the mathematical representation of a 3D scene into a 2D image. This image is comprised of a rectangular grid of pixels, the colors of which are computed individually. The process of computing the color of a pixel is known as shading.
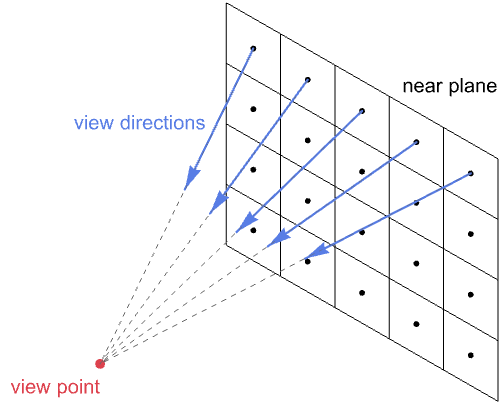
One can think of these pixels as embedded within the 3D scene on a small plane just in front of the view point. This plane is known as the near plane. Each pixel has a corresponding view direction vector originating from its center toward the view point.
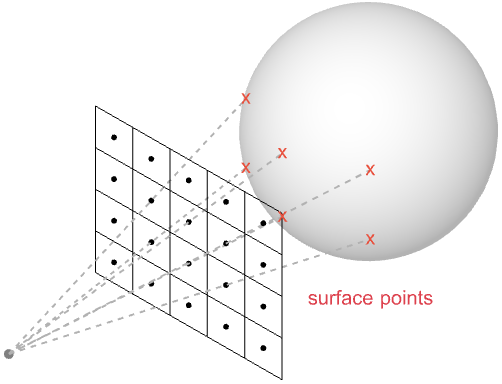
The color of a pixel is determined by the amount of incoming light that passes through the pixel's center along its view direction. The light entering a pixel must come from the surface of an object in the scene—either emitted by the surface directly or reflected off it from some other light source. Since our assumption is that light travels in a straight line, each pixel has at most one surface point in the scene that directs light both through its center and along its view direction.*
*Note that this assumes all surfaces are opaque. For transparent surfaces, multiple points may need to be considered.
There are two common ways to determine the surface point corresponding with a given pixel. For offline renders, ray tracing is typically used to cast a ray from the center of a pixel along its negative view direction. If it intersects with a surface, the corresponding hit point is the desired surface point.
For real-time renders, the most common technique is to project all surfaces onto the near plane by applying a sequence of linear transformations to the scene geometry. This is followed by a rasterization and interpolation step to determine the exact surface point for each pixel.
Regardless of the method used, the resulting surface points are the same.
Once the surface point is known, the color of the pixel is given by the amount of outgoing light from that point along the pixel's view direction. The amount of this outgoing light is determined by the reflectance equation.
The Reflectance Equation
The global distribution of light in a scene is described by the rendering equation. For the purposes of PBR, a localized variant of this equation is used, called the reflectance equation.
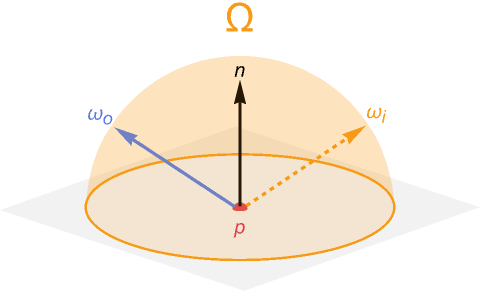
At a high level, the reflectance equation for opaque surfaces is defined as
This equation describes the amount of outgoing light from a point on a surface ![]() toward a specific direction
toward a specific direction ![]() . This amount of light is called the radiance of that point.
. This amount of light is called the radiance of that point.
This radiance is a spectral quantity, meaning it consists of a variety of different wavelengths (i.e. colors) of light. When taking measurements of real-world light sources, this radiance is often described using a spectral power distribution (SPD). This SPD gives the intensity of the light over the entire visible spectrum.
Storing and performing calculations on these distributions would be computationally expensive. Instead, graphics programs store radiance as a 3D vector, the channels of which signify the intensity of red, green and blue wavelengths of light. Due to the way humans perceive color, these three wavelengths of light can be combined to form most of the visible spectrum.
Looking at the reflectance equation, it states that the radiance of outgoing light is the sum of the light emitted by the surface and the light reflected by it. The following sections will cover these two contributions of light in detail.
Emitted Light (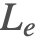 )
)
Emitted light is light generated by the surface itself. In real life, this is often the result of blackbody radiation, which causes hot objects to glow.
In most graphics programs, this light is specified directly by the user in the form of an RGB color. Therefore, determining the amount of emitted light is trivial, as one simply returns the specified color.
In the Wolfram Language's default lighting system, emitted light is specified by Glow. For MaterialShading, the "EmissionColor" parameter is used.
Reflected Light (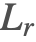 )
)
Reflected light includes all light incident on the surface point from elsewhere in the scene that then gets redirected in the outgoing direction. This contribution of light is responsible for our ability to see most objects, as they are typically too cold to emit blackbody radiation within the visible spectrum for humans.
It is common to see the reflected light term expanded into its full integral form.
The geometric representation of this equation is shown in the following:
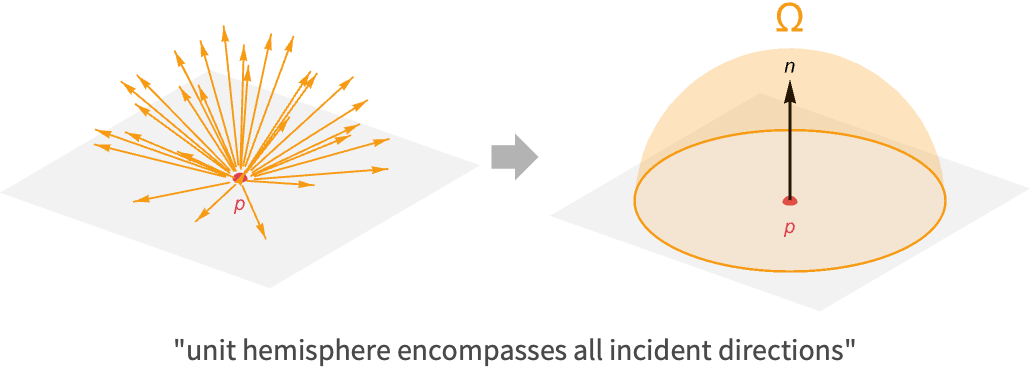
The integral comes from the fact that we must consider all possible directions of incoming light for a given surface point. Conveniently, the set of all these possible directions can be described by the unit hemisphere aligned with the surface normal at this point. Any direction outside of this hemisphere is coming from behind the surface, and therefore will not contribute to the radiance of opaque materials.
Unfortunately, this integral cannot be solved analytically for an arbitrary scene. Instead, the integral must either be approximated numerically, or additional assumptions must be made to simplify it.
A common numerical approximation for offline renders that use ray tracing is to perform Monte Carlo sampling over the hemisphere. This may be followed by a denoising stage to clean up the final image. Further optimizations such as importance sampling can be used to reduce the number of samples needed.
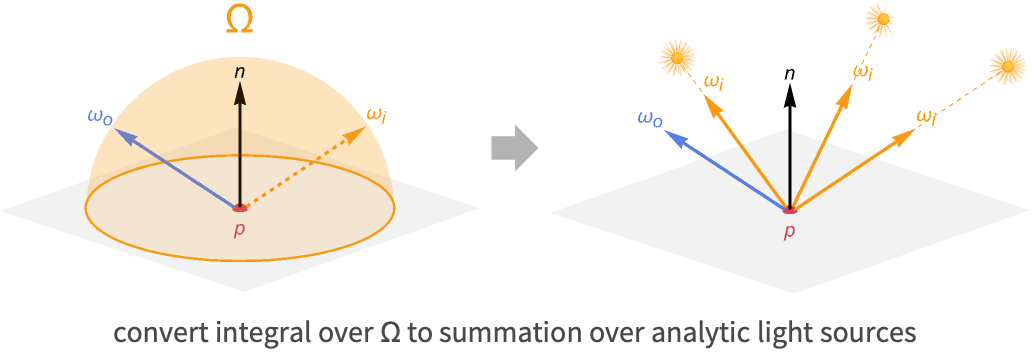
Real-time applications typically make a simplifying assumption regarding light sources that allows the integral to be solved analytically. This assumption is that light incident to a surface can only come from special light sources and not from other surfaces in the scene. These special light sources are referred to as analytic lights. The three common types of analytic lights are directional lights, point lights and spot lights.
By only using analytic light sources, the integral over the hemisphere can be converted to a summation over all lights in the scene.
Now that we have a computationally feasible formulation for reflected light, we can cover the three terms contained in its summation. The following sections will cover these terms in detail; however, a brief description is provided below:
1. ![]() — Radiance from the incoming direction.
— Radiance from the incoming direction.
2. ![]() — Fraction of radiance after being projected across the surface.
— Fraction of radiance after being projected across the surface.
3. ![]() — Fraction of incident radiance redirected in the outgoing direction.
— Fraction of incident radiance redirected in the outgoing direction.
The ![]() term can be thought of as the maximum radiance that then gets attenuated by the remaining two terms.
term can be thought of as the maximum radiance that then gets attenuated by the remaining two terms.
Incident Light (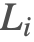 )
)
The incident light term provides the radiance from a given light to a particular surface point. Due to energy conservation, this term represents the maximum radiance that can be reflected by the surface from this light source.
The radiance from an analytical light depends on its type. In the Wolfram Language, the radiance of each light is defined as follows:
1. Directional — Radiance is the color of the light.
2. Point — Radiance is the color attenuated by the distance to the light.
3. Spot — Radiance is the color attenuated by both the distance and angle to the light.
The examples following show a square being lit by an overhead white light of each type. The attenuation present in the point and spot lights should be apparent.
See Lighting for more information on lighting specification and calculations.
Lambert's Cosine Law (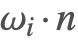 )
)
The dot product between the incident direction (![]() ) and surface normal (
) and surface normal (![]() ) attenuates the radiance of the incident light in accordance with Lambert's cosine law.
) attenuates the radiance of the incident light in accordance with Lambert's cosine law.
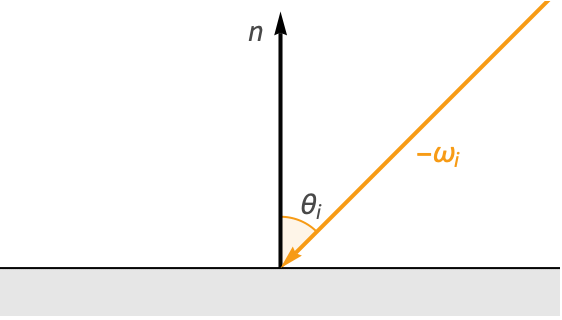
When light hits a surface, the angle it makes relative to the surface normal is known as the angle of incidence (![]() ).
).
According to Lambert's cosine law, the diffuse radiance at this point due to this incident light will be directly proportional to the cosine of the angle of incidence (![]() ).
).
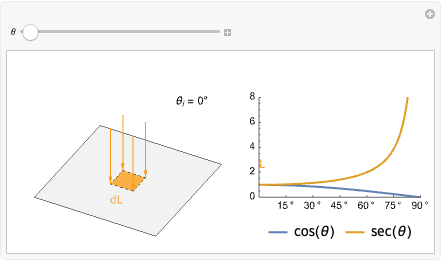
To understand the reason behind this, imagine a small 2D patch on the surface of the object. If a beam of light hits this patch perpendicular to the surface (![]() ), then all the radiance of that light beam hits our small patch. However, as the angle of incidence increases, the projected area of the light beam increases as well, stretching beyond the area of the patch. This causes the light's radiance to spread out across the surface, meaning our patch receives less radiance overall.
), then all the radiance of that light beam hits our small patch. However, as the angle of incidence increases, the projected area of the light beam increases as well, stretching beyond the area of the patch. This causes the light's radiance to spread out across the surface, meaning our patch receives less radiance overall.
If our imaginary patch is a unit square, then the projected area will be equal to ![]() . This means the radiance received by the original patch is
. This means the radiance received by the original patch is ![]() .
.
Notice that when the angle of incidence reaches 90°, the light beam will be parallel to the surface, and therefore our patch will receive no radiance and remain dark.
Lambert's cosine law is responsible for the familiar shading of matte surfaces and is even common in non-PBR implementations. For example, the lighting on the sphere following is calculated using only Lambert's cosine law with a single directional light source from above.
In practice, the cosine of the angle of incidence is calculated by taking the dot product of the incident direction and surface normal. These two operations are equivalent as long as both vectors are normalized. This is why the equation for reflected light is sometimes written with a cosine term instead.
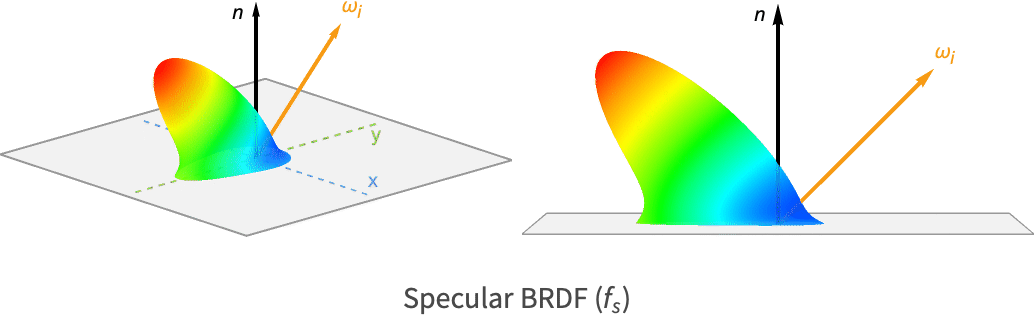
Bidirectional Reflectance Distribution Function ( )
)
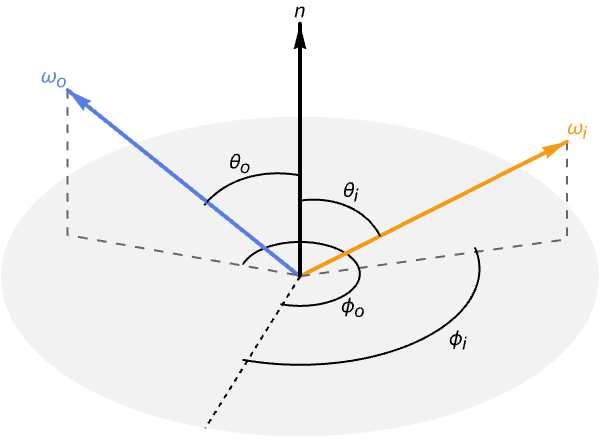
The final term for reflected light is the bidirectional reflectance distribution function (BRDF). The BRDF determines the ratio of incident light at the surface point that gets redirected in the outgoing direction. In contrast to the previous terms, this function is unique to different material types.
The BRDF is a function of three vectors: the incident direction (![]() ), outgoing direction (
), outgoing direction (![]() ) and surface normal (
) and surface normal (![]() ). The surface normal is often omitted, in which case it is implied that the normal lies along the positive
). The surface normal is often omitted, in which case it is implied that the normal lies along the positive ![]() axis.
axis.
An equivalent parameterization also exists that uses the azimuth (![]() ) and zenith (
) and zenith (![]() ) angles of the incident and outgoing directions relative to the surface normal.
) angles of the incident and outgoing directions relative to the surface normal.
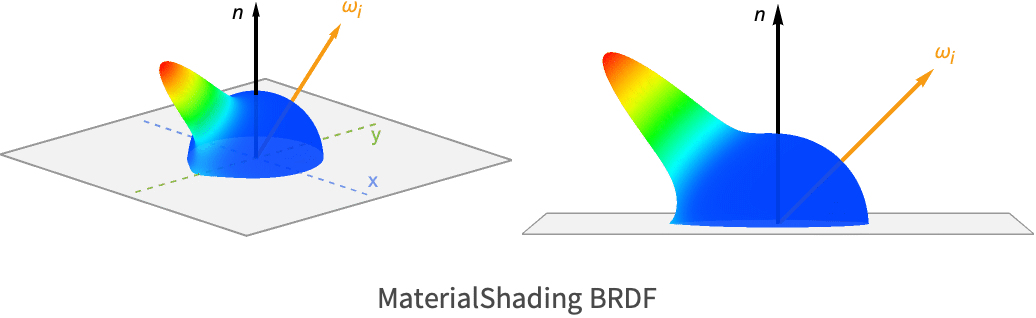
Using special equipment, the BRDF can be directly measured for real-world materials. One notable example is the analysis done by Mitsubishi [1]. The following shows the BRDF they measured for a piece of PVC. For the visualization, the incident direction is held constant while the outgoing direction is varied to cover the entire hemisphere. The size and color of the lobe denote how much light was reflected in that direction.
Directly using the measured BRDF data of real materials is not practical for most renderers. Some reasons include:
1. Measuring new materials requires specialized equipment and access to the material itself.
2. Rendering would require large amounts of data, making real-time calculations on the GPU problematic.
3. Each measured BRDF is highly specific to the measured material and cannot be easily modified.
Because of this, graphics programs opt to use parametric BRDFs that can approximate a wide range of materials. The measured data can then be used as a benchmark to compare against various parametric BRDF models. Once a suitable parameterization has been found, it is easy for designers to tweak the parameters to achieve the appearance of the desired material.
A specific instance of the full parametric BRDF used by MaterialShading is shown here:
The following sections will cover the various aspects of this BRDF.
A tale of two BRDFs
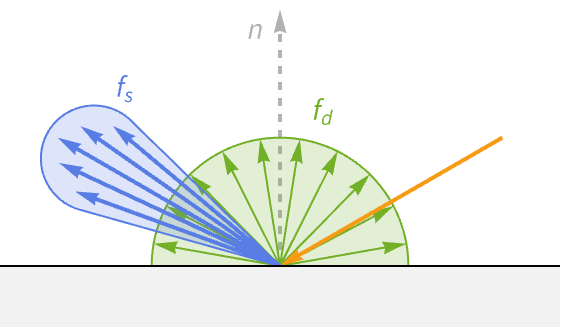
In practice, graphics programs do not use one, but rather two separate parametric BRDFs that sum together to create the full BRDF of the material. These are referred to as the specular and diffuse BRDFs, and they represent two distinct behaviors of light when it hits a surface—refraction and reflection.
Reflected light bounces off the surface in the ideal reflection direction. Meanwhile, refracted light enters the surface at a skewed angle determined by both the index of refraction (IOR) of the medium it is leaving and the one it is entering.
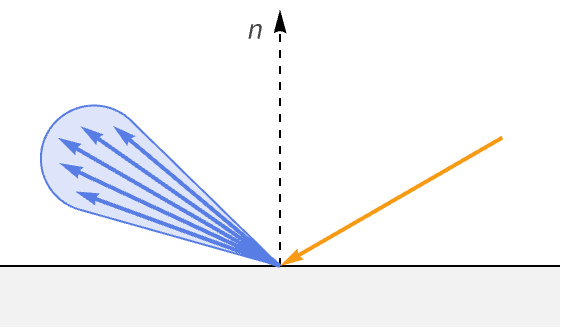
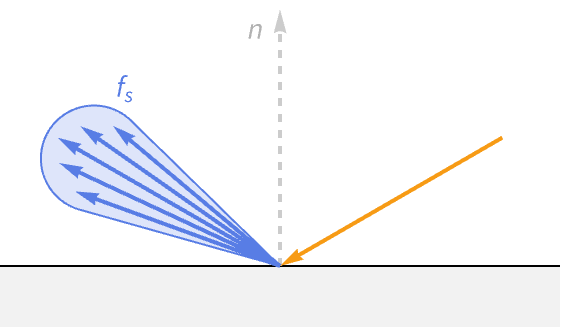
Reflected light
Reflected light reflects off the surface as if it were a perfect mirror, following the ideal reflection direction. This light is referred to as specular light, based on the Latin word speculum, meaning mirror. Specular light is responsible for the bright highlight seen on smooth objects. The highlight is visible where the angle toward the viewer aligns with the angle of reflection. Because of this, specular light is dependent on the direction of the viewer.
Refracted light
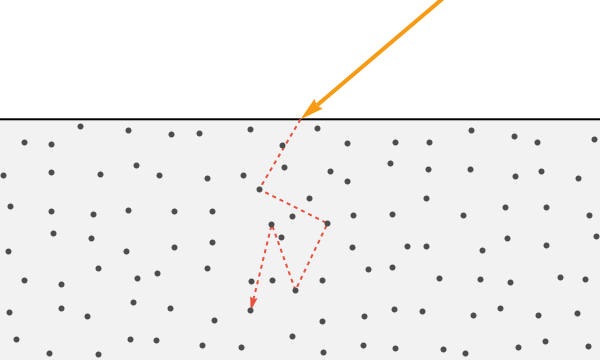
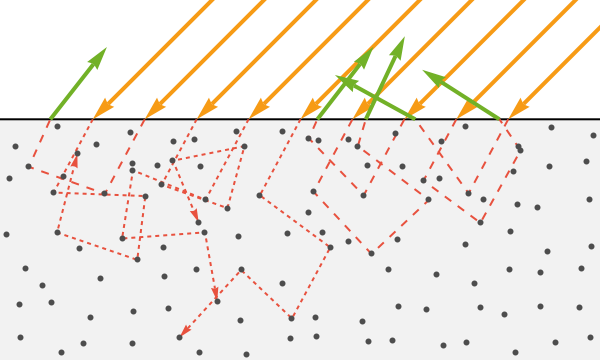
Refracted light takes a more complicated route. After entering the surface, it continues to interact with particles in the material. Each interaction causes it to further scatter and lose energy. If a ray of light loses all of its energy, it is considered to be absorbed by the material (i.e. converted to heat).
However, some of this scattered light manages to escape the surface. Having undergone so much scattering, this light's direction is effectively random.
When considering a large number of these escaping light rays, they appear spread out equally in all directions. Because of this, this light is called diffuse light.
For most opaque materials, the refracted light penetrates less than a few nanometers beneath the surface. This also means that the portion that exits the surface does so near its entry point (i.e. within the width of a pixel). Because of this, graphics programs typically make the assumption that the diffuse light emanates from the entry point.
For translucent materials like skin, the refracted light penetrates significantly deeper and exits further from its entry point. This effect is referred to as subsurface scattering and requires additional techniques to achieve. Similarly, transparent materials like glass transmit the refracted light with minimal absorption before exiting the back side of the object. This effect is called transmission and also requires additional techniques to achieve.
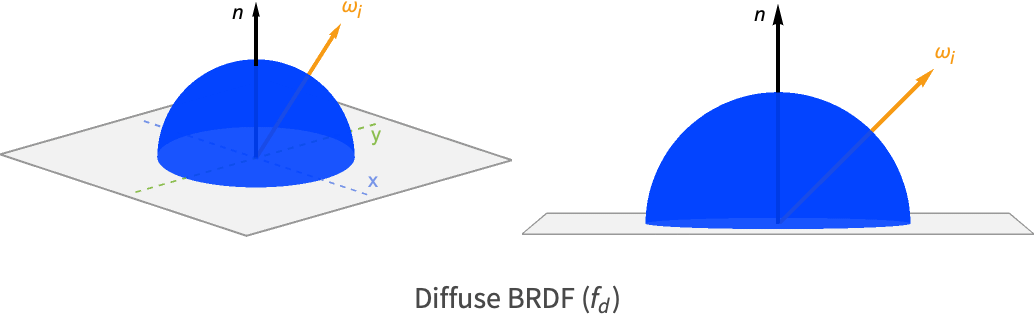
Diffuse BRDF
The diffuse BRDF is responsible for modeling the refracted portion of light that escapes the surface in close proximity to the point where it entered.
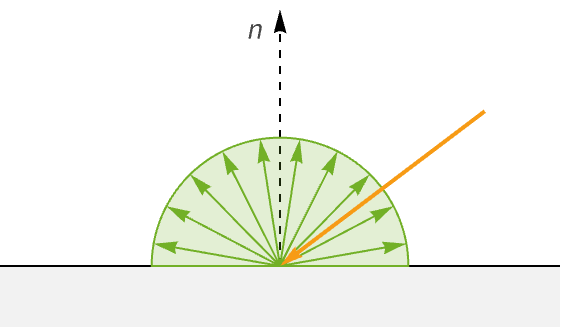
The Lambertian BRDF is the common choice for the diffuse BRDF and it is the one implemented by MaterialShading. It is defined as:
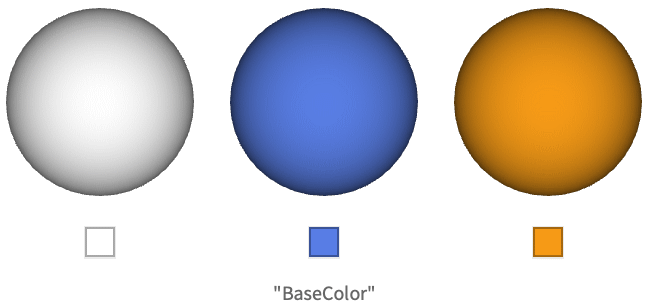
In the context of computer graphics, the albedo color gives the color of diffuse light reflected from the surface when lit with incident light of unit radiance perpendicular to the surface. In other words, it is the color of the surface without any lighting applied. Note that the scaling by ![]() is for the purpose of energy conservation.
is for the purpose of energy conservation.
The diffuse lobe formed by this BRDF is simply a hemisphere, as its value is not dependent on the position of the viewer or light source.
For MaterialShading, the albedo color is specified by the "BaseColor" parameter.
Specular BRDF
In contrast to the diffuse BRDF, the specular BRDF is somewhat complex and will require knowing some theory before diving into the final equation.
By definition, specular light is that which reflects off the surface in the ideal reflection direction. However, if this were true, then the highlight on smooth objects like spheres would only exist at the single infinitesimal point where the view direction and incident direction align. But this is not the case for real-world materials, which can exhibit glossy highlights that cover a reasonable portion of the object's surface.
This dissonance can be explained by the existence of microfacets.
Microfacet theory
The microfacet theory used by nearly all specular BRDFs suggests that while surfaces may appear smooth at the macro level, at the micro level they consist of a large amount of microfacets. Each microfacet is optically flat, meaning when hit by a ray of light, it will reflect it in the ideal reflection direction.
Therefore, the variance in specular reflections is caused by the variance in directions of these microfacets. This explains why surfaces that appear smooth at the macro level can still return a specular lobe with variance about the ideal reflection direction.
While the choice of diffuse BRDF is almost universal across PBR implementations, the specular BRDF has a variety of options to choose from. However, since each version adheres to the microfacet theory, they all follow the same structure shown in the following.
An example lobe for this specular BRDF is shown in the following:
This structure contains three terms describing how light interacts with the microfacets. The choice of each term is up to the graphics program, where there is often a tradeoff between physical accuracy and performance.
A short description of each term is provided:
• Distribution term — How much of the surface is oriented to reflect light in the outgoing direction.
• Geometry term — How much of the surface is not shadowed or masked by other parts of the surface.
• Fresnel term — Percentage of incident light that gets reflected (and therefore not refracted).
Before diving into each term, we must first cover the concepts of roughness and anisotropy in the context of microfacets.
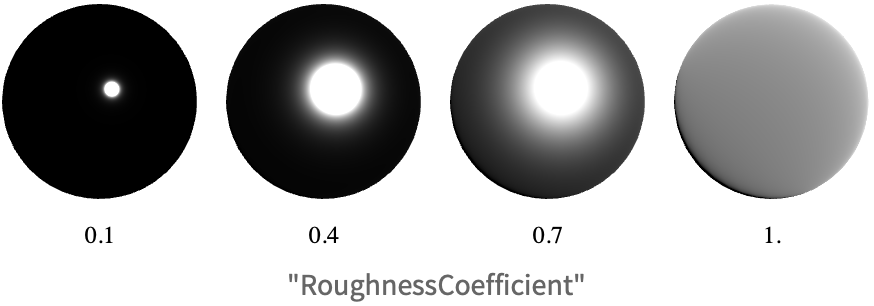
Roughness
Both the distribution term (![]() ) and geometry term (
) and geometry term (![]() ) require a parameter
) require a parameter ![]() that describes the roughness of the surface. At the microfacet level, this roughness corresponds to the variance of the orientations of microfacets. Note that when describing the orientation of microfacets, we are really describing the direction of their surface normals.
that describes the roughness of the surface. At the microfacet level, this roughness corresponds to the variance of the orientations of microfacets. Note that when describing the orientation of microfacets, we are really describing the direction of their surface normals.
The more varied the microfacet normals, the more scattered the light becomes. When ![]() , all microfacet normals are aligned with the macro-surface normal, which produces perfect mirror reflections. As
, all microfacet normals are aligned with the macro-surface normal, which produces perfect mirror reflections. As ![]() approaches 1, the microfacet normals are oriented almost at random, which causes reflected light to be more diffuse in nature.
approaches 1, the microfacet normals are oriented almost at random, which causes reflected light to be more diffuse in nature.
Instead of specifying this ![]() term directly, it is common to take a roughness parameter as input and remap it to
term directly, it is common to take a roughness parameter as input and remap it to ![]() in order to make the roughness perceptually linear.
in order to make the roughness perceptually linear.
This roughness parameter corresponds to the "RoughnessCoefficient" parameter for MaterialShading.
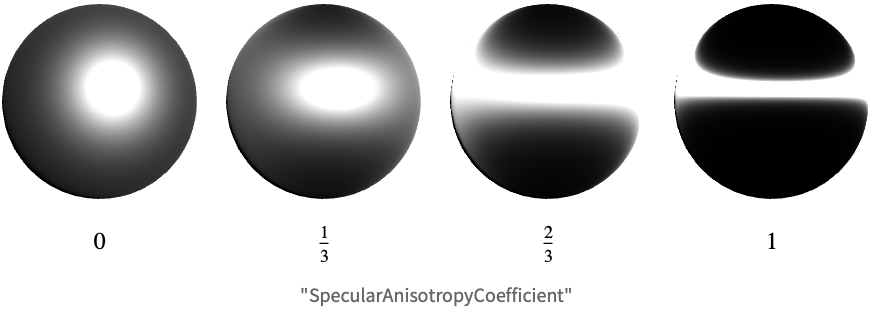
Anisotropy
It is common for graphics programs to assume all materials are isotropic, meaning they reflect light the same regardless of the angle they are viewed from. At the micro-surface level, this implies the direction of the microfacet normals shows no preference for any particular direction.
However, some real-world materials do show strong preference for reflecting light along one direction. These materials are called anisotropic and include materials like brushed metals and wood.
This effect is implemented in the specular BRDF by considering two values for ![]() , one along the tangent direction and one along the bitangent direction. These values are denoted by
, one along the tangent direction and one along the bitangent direction. These values are denoted by ![]() and
and ![]() , respectively.
, respectively.
Like the ![]() value, the user does not specify
value, the user does not specify ![]() and
and ![]() directly, but instead passes a property called anisotropy, which is used alongside the roughness to calculate the anisotropic
directly, but instead passes a property called anisotropy, which is used alongside the roughness to calculate the anisotropic ![]() values.
values.
In MaterialShading, the anisotropy for the specular reflection is controlled by the "SpecularAnisotropyCoefficient" parameter.
By default, the tangent direction is calculated to be horizontal with respect to the viewer. This direction can be adjusted by specifying an angle along with the "SpecularAnisotropyCoefficient" property.
With the knowledge of roughness and anisotropy, we can finally dive into the first term of the specular BRDF.
(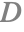 ) Distribution term
) Distribution term
As we saw in the previous sections, specular light always reflects in the ideal reflection direction (![]() ). Therefore, in order to determine the amount of light reflected off a surface in a specific direction, one must first determine the ratio of microfacets that are oriented in such a way as to reflect light in that direction.
). Therefore, in order to determine the amount of light reflected off a surface in a specific direction, one must first determine the ratio of microfacets that are oriented in such a way as to reflect light in that direction.
This is given by the distribution term, which describes how the microfacet normals are distributed relative to the macro-surface normal. This term is also known as the normal distribution function (NDF).
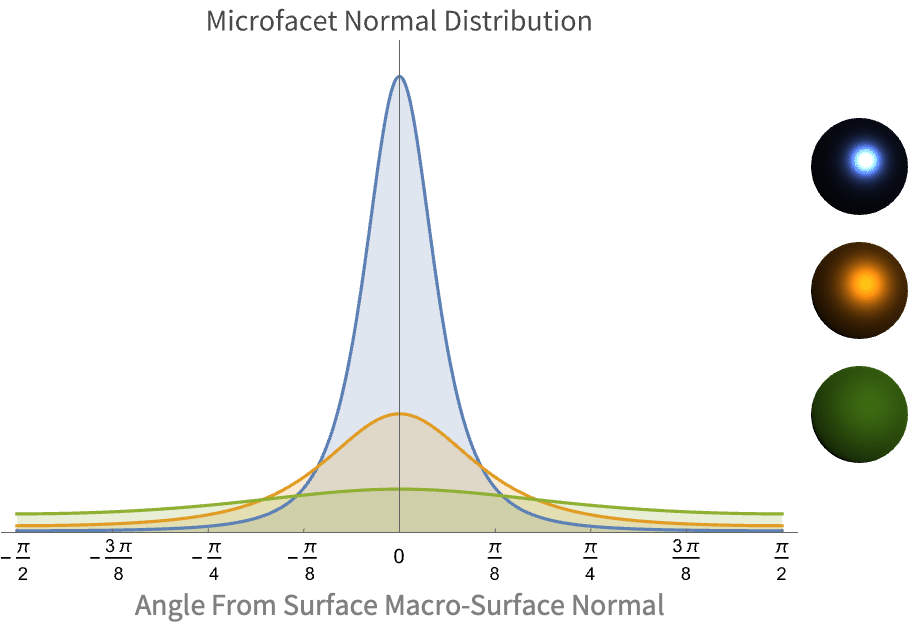
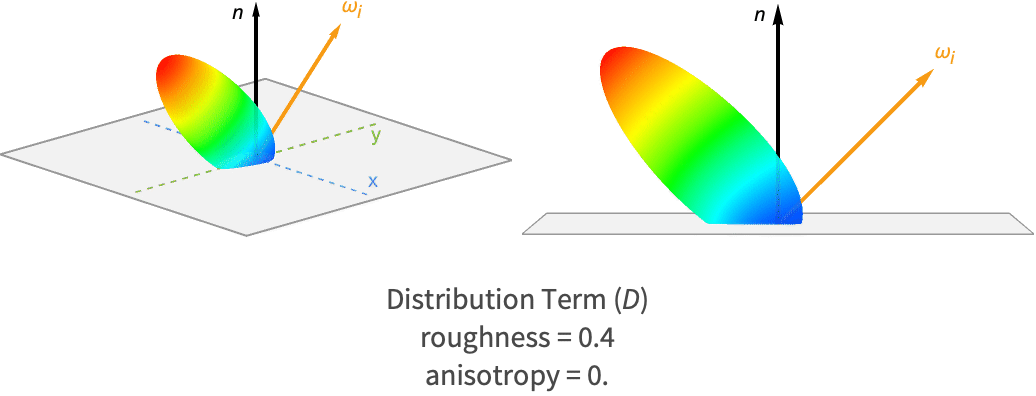
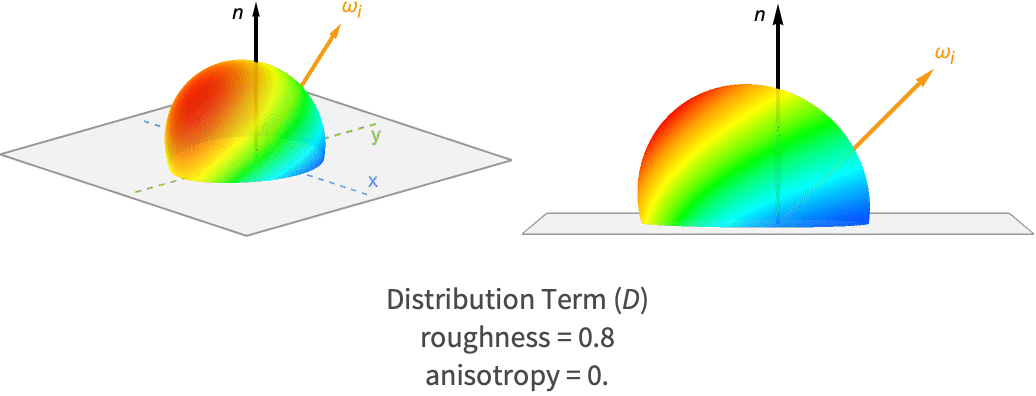
An example of this distribution with varying levels of roughness is shown in the following, along with the corresponding renders.
Notice how much of the micro-surface normals is concentrated around the macro-surface normal (0 on the plot). For smooth materials (blue), the concentration drops off quickly as the angle increases. Meanwhile, rougher materials (green) show a more uniform concentration of microfacet normals, hinting at their diffuse nature.
The specular BRDF samples a specific angle from this distribution to become the distribution term. This is the angle between the macro-surface normal and the normal direction of microfacets that would reflect light from the incident direction toward the outgoing direction. According to the law of reflection, this normal direction must lie halfway between the incident direction and outgoing direction. Because of this, it is often called the halfway vector and is computed as follows:
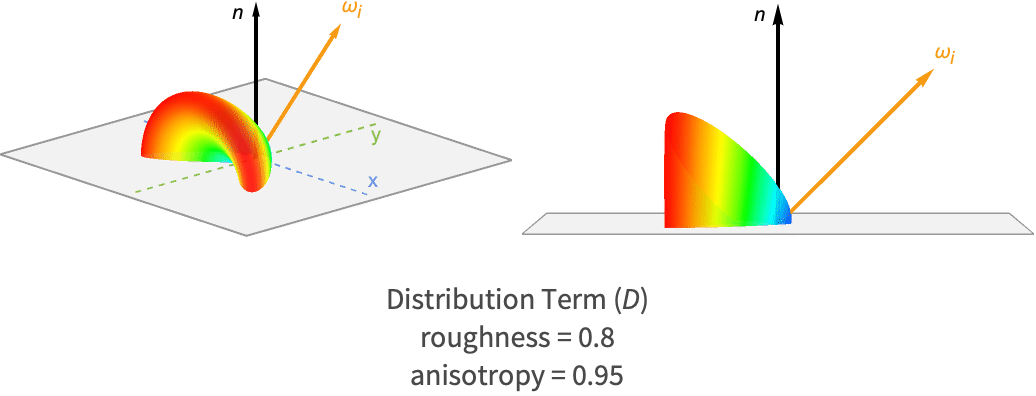
For anisotropic materials, the distribution term must consider how this halfway vector aligns with the tangent and bitangent directions, since for anisotropic materials, the roughness will vary depending on these directions.
The distribution term used by MaterialShading is the Burley [2], which is the same formulation used by Walt Disney Animation Studios. It is defined as:
Note that in the case of isotropic materials, ![]() .
.
The lobe created by this term alone is shown for a few combinations of roughness and anisotropy.
( ) Geometry term
) Geometry term
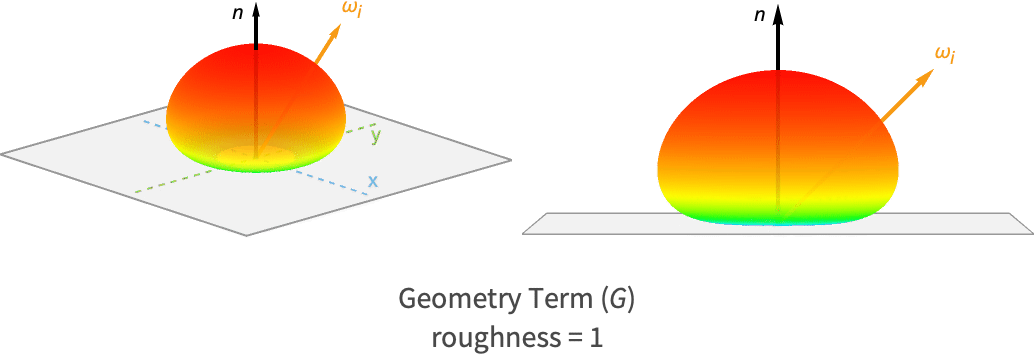
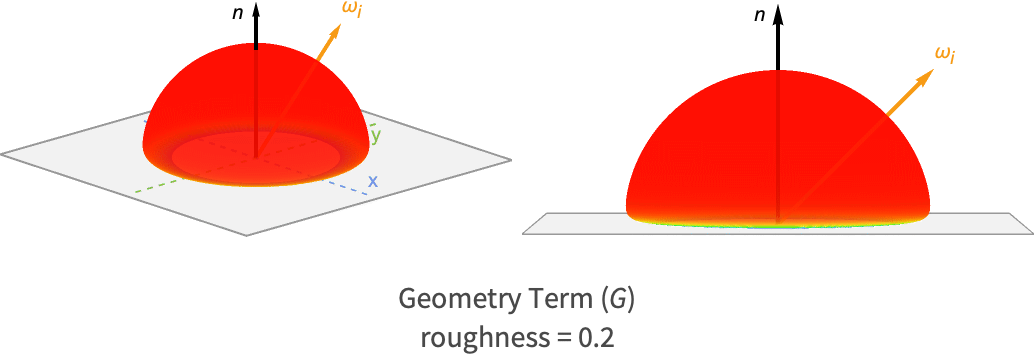
The geometry term takes into account the microfacets that are shadowed or masked by other microfacets and therefore do not contribute to the final reflected light.
Microfacets are shadowed when another microfacet blocks their path toward the light source. Similarly, masking takes place when a microfacet is not visible to the viewer because there is another microfacet occluding it.
For its geometry term, MaterialShading uses the GGX–Smith height-correlated masking and shadowing function [3]:
Note: This term is not affected by anisotropy. If the material is anisotropic, the two ![]() values are averaged to get the single
values are averaged to get the single ![]() value for this equation.
value for this equation.
The lobe for this component of the specular BRDF is shown following for a rough and smooth surface.
Notice how the rougher surface produces much smaller values at grazing angles compared to the smooth surface. This makes sense due to the fact that microfacets with zero variance will produce no masking or shadowing, while higher-variance microfacets are more likely to mask/shadow other microfacets at low angles.
(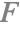 ) Fresnel term
) Fresnel term
Earlier in this document, we covered how light splits into two components when crossing from one medium to another—refraction and reflection. However, the light is not always split into these two components evenly.
The Fresnel equations describe how much of the incoming light is reflected versus refracted. This ratio is determined both by the angle of incidence and the index of refraction of the two media. For the purposes of rendering, these media are often air and the material of an object in the scene.
The Fresnel equations assume that the light is incident on an optically flat surface. Therefore, it applies to each microfacet individually (unlike the distribution and geometry terms, which assume some statistical distribution of microfacets).
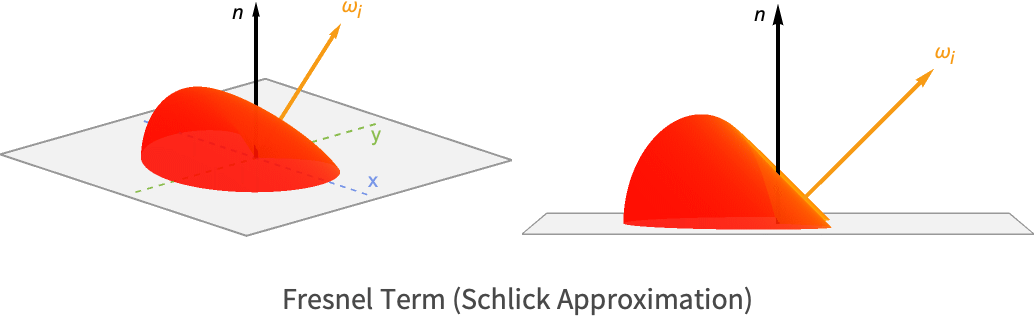
In practice, it is common to use an approximated version of these equations called the Schlick approximation.
Here ![]() represents the specular reflectance at normal incidence (light hitting perpendicular to a surface). Meanwhile,
represents the specular reflectance at normal incidence (light hitting perpendicular to a surface). Meanwhile, ![]() is the specular reflectance at the grazing angles.
is the specular reflectance at the grazing angles.
In reality, the specular reflectance at grazing angles for all materials is 1.0. This behavior is called the Fresnel effect, and is particularly noticeable when looking across a large flat surface, such as a large body of still water.
For this reason, the equation is usually written with 1 substituted in for ![]() .
.
The lobe for the Schlick approximation is shown following for an especially dark material. Notice how the reflectance increases at grazing angles.
The value of the specular reflectance at normal incidence is officially calculated using the indices of refraction of both media.
One complication is that the IOR of a material changes based on the wavelength (i.e. color) of light. Therefore, ![]() of each RGB color channel would need to be calculated separately.
of each RGB color channel would need to be calculated separately.
In practice, the three values for ![]() are often set directly by the user as an RGB color.
are often set directly by the user as an RGB color.
MaterialShading uses the Schlick approximation for dielectric (non-metallic) materials. The value ![]() is controlled by the "SpecularColor" property. For real-world dielectric materials, this value is very low, at around 0.04 for all three (3) color channels.
is controlled by the "SpecularColor" property. For real-world dielectric materials, this value is very low, at around 0.04 for all three (3) color channels.
The approximation used for metallic materials is more complex. Before going over it, we will briefly touch on the difference between metals and non-metals in the context of computer graphics.
Conductors vs. dielectrics
Physically based shading models often follow a metallic workflow, which distinguishes between metallic materials (conductors) and nonmetallic materials (dielectrics). Diffuse and specular light behave so differently between these two material types that they warrant different calculations.
Dielectrics (non-metals)
Dielectrics are the most common type of material, including things like plastic, stone, wood and leather. These materials will reflect light without modifying its color. However, when the light is refracted, certain wavelengths get absorbed, while the rest are emitted, thus changing its color. This altering of the diffuse light is what gives these materials their familiar colors. For example, we view bananas as being yellow because they tend to absorb the other wavelengths of light, leaving only the yellow light to be emitted as their diffuse color.
Conductors (metals)
Conductors include all the metals, including gold, copper, steel and bronze. These materials have the unique property of absorbing all of their refracted light. Thus, they have no diffuse color. Meanwhile, they still reflect light, though they alter its color. How the metal alters this reflected light will determine the color we perceive the metal as being. For example, gold causes white light to have a yellow tint, while copper has a reddish tint. If a metal reflects all wavelengths about the same, then it will appear as some shade of gray, such as iron and aluminum.
(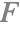 ) Fresnel term for conductors
) Fresnel term for conductors
The Schlick approximation is useful for dielectric materials, where the specular highlight has a small contribution to the final appearance. However for conductors (i.e. metals), the specular component makes up the entirety of their appearance. Therefore, it is beneficial to use a more accurate approximation for those materials.
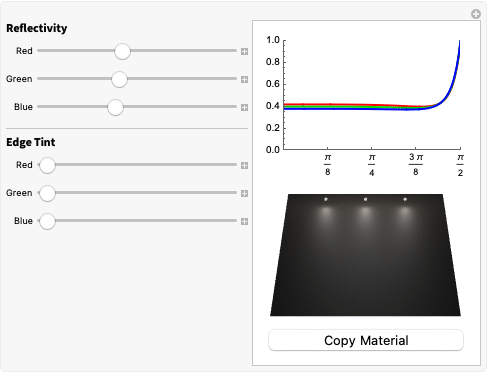
MaterialShading uses the dielectric-conductor Fresnel formulation described by Sébastien Lagarde [4]. His formulation relies on both the IOR and extinction coefficient to approximate the reflectivity curve of the material.
However, setting the values of these properties for each RGB channel directly would not be intuitive when trying to match a material from a visual reference. Therefore, MaterialShading also uses an intermediate layer that calculates the IOR and extinction coefficient from a reflectivity color and edge tint. The reflectivity color describes the color of specular reflection for the majority of the surface, while the edge tint determines the tint of the light at grazing angles (typically at the edge of objects).
MaterialShading uses the reflectivity and edge tint mapping described by Gulbrandsen [5].
The example following shows the reflectance for red, green and blue wavelengths of light, controlled by these reflectivity and edge tint parameters. Notice that increasing the edge tint for a specific wavelength causes that color to be more prominent at grazing angles.
For MaterialShading, the reflectivity and edge tint for metallic materials are set by the "BaseColor" and "SpecularColor" parameters, respectively.
Additional Effects
The parametric BRDF we have seen so far does a good job approximating materials with a single opaque layer. However, we can make some modifications to increase the types of materials it can approximate.
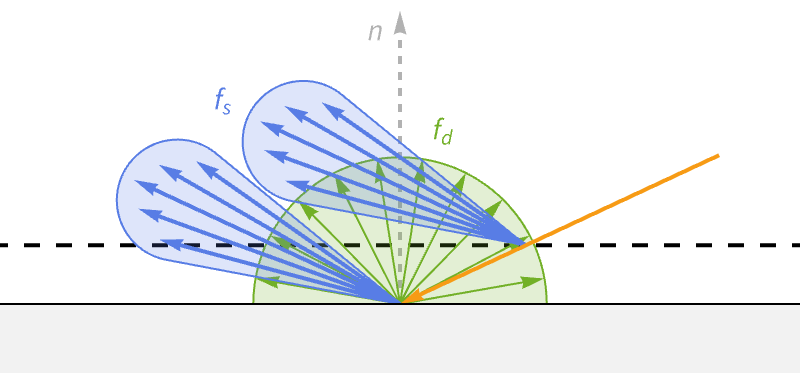
Coat
It is common for some materials to have a thin clear coat covering the base surface. This coat is often made of lacquer or polyurethane in the cases of car paint and finished wood. This coat makes the surface appear shinier due to additional reflection.
In PBS, this effect is achieved by assuming the existence of a secondary specular layer just above the base surface. Now we split the incoming light twice—once at the coat layer and again at the base surface.
The specular component of the coat layer uses the dielectric specular BRDF, since the coating is assumed to be non-metallic. Unlike the base layer, the light that gets transmitted through the coat does not contribute to a diffuse lobe, but instead travels to the base surface and gets used by the specular and diffuse BRDFs of the base surface.
In MaterialShading, a coat can be specified using the "CoatColor" parameter. When a coat is specified, the additional properties "CoatRoughnessCoefficient" and "CoatAnisotropyCoefficient" can be used and correspond to the "RoughnessCoefficient" and "SpecularAnisotropyCoefficient" properties of the base surface.
The following examples show a white object with different coat specifications:
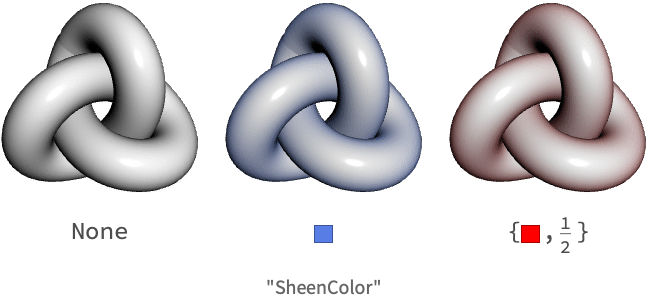
Sheen
Some fabrics consist of numerous fibers that stand perpendicular to the macro-surface. At grazing angles, the edges of these fibers tend to align with the outgoing direction and cause backscatter. This creates the highlights around the rim of materials like velvet.
This effect is achieved using an additional BRDF with a distribution term catered to these types of materials. MaterialShading uses the sheen BRDF described by Sony Pictures [6]:
In MaterialShading, sheen can be specified using the "SheenColor" property. When a sheen color is specified, the additional property "SheenRoughnessCoefficient" can be used to determine the roughness of the sheen lighting.
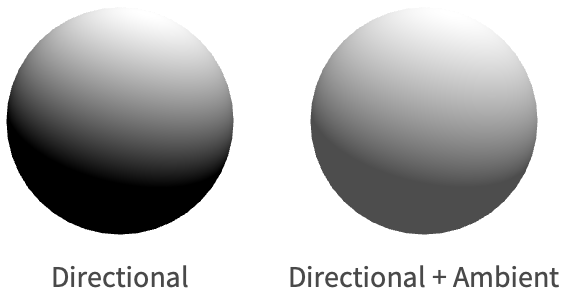
Ambient Lighting
So far we have only discussed the three analytic lights—directional, point and spot lights. These are also sometimes referred to as direct lights, because they cast light directly from a light source to the surface.
However, in the real world a significant amount of light incident on a surface is indirect light. This is light that has been reflected off of one or more other surfaces before reaching the current surface. The process of simulating this indirect light is known as global illumination (GI), and there is a variety of methods used to achieve it.
For real-time renderers, one cheap yet effective method is the use of an ambient term. This term is added to the resulting outgoing radiance of the reflectance equation to approximate a constant incoming radiance from all directions. In the Wolfram Language, this term is set by specifying an "Ambient" light.
Both the default system appearance and MaterialShading support ambient lights. However, MaterialShading also allows the user to set the ambient occlusion of the surface.
Ambient occlusion is the phenomenon where the corners and crevices of objects tend to be darker since they do not receive as much indirect light as the rest of the surface. For MaterialShading, the fraction of ambient light exposed to the surface of a material can be set with the "AmbientExposureFraction" parameter. However, this parameter is usually only used with a texture to accurately map the cracks of the material to the surface of the object.
References
1. Ngan, A., F. Durando and W. Matusik. Experimental Analysis of BRDF Models. The Eurographics Association (2005).
2. Burley, B. Physically-Based Shading at Disney. Walt Disney Animation Studios (2012).
3. Heitz, E. "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs." Journal of Computer Graphics Techniques, Williams College (2014).
4. Lagarde, S. Memo on Fresnel Equations. 2013. https://seblagarde.wordpress.com/2013/04/29/memo-on-fresnel-equations.
5. Gulbrandsen, O. "Artist Friendly Metallic Fresnel." Journal of Computer Graphics Techniques (JCGT) 3, no. 4 (2014): 64–72.
6. Estevez, A. and C. Kulla. Production Friendly Microfacet Sheen BRDF. Sony Pictures Imageworks (2017).
7. Smythe, D. and J. Stone. MaterialX: An Open Standard for Network-Based CG Object Looks, Version 1.38, 2021.