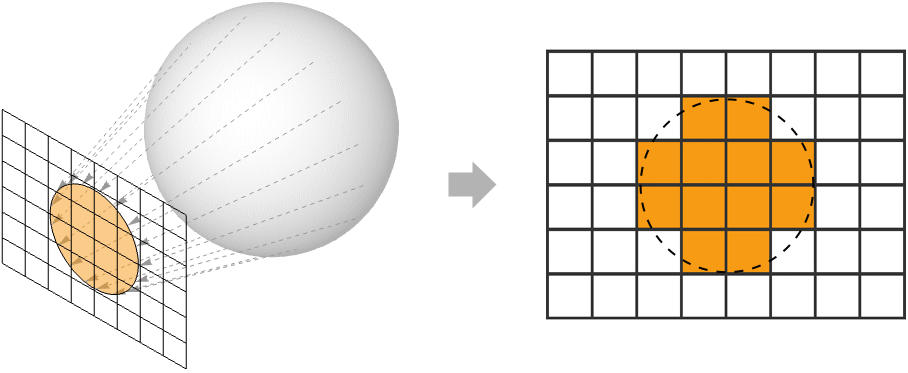
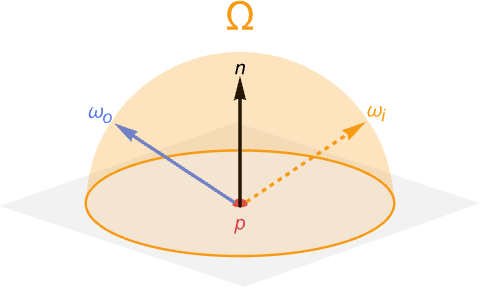
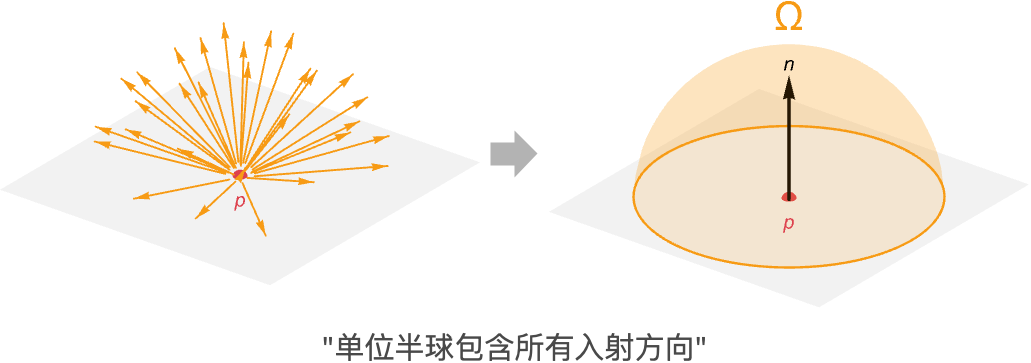
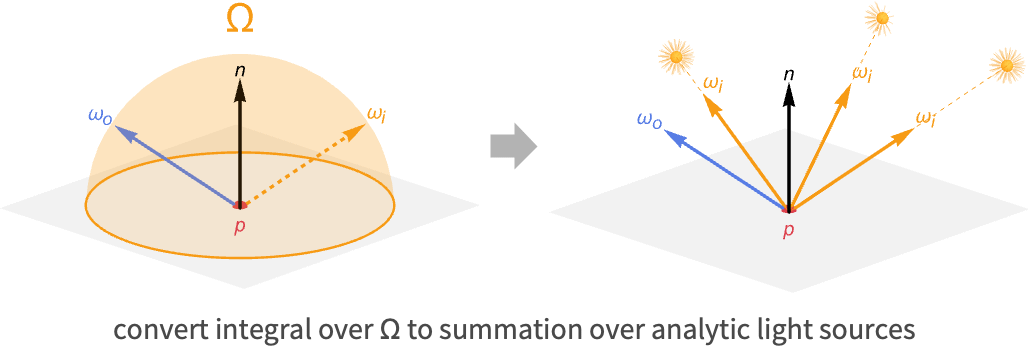
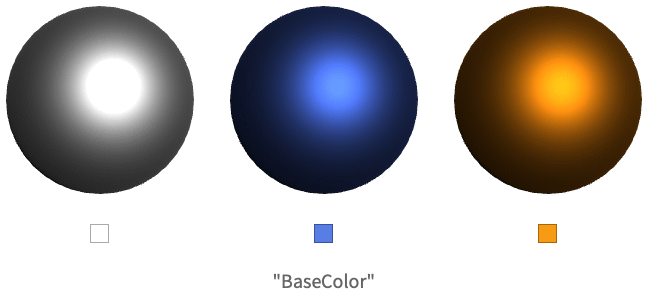
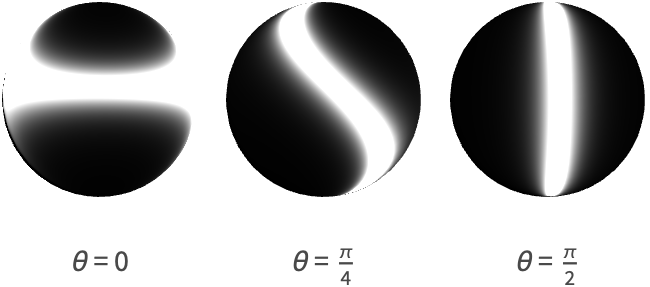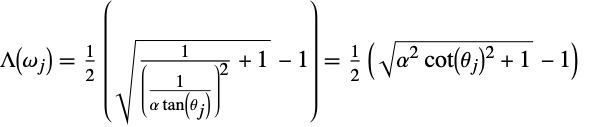基于物理的渲染
基于物理的渲染 (PBR) 是一种计算机图形学方法，旨在通过模拟现实世界中的光行为来渲染图像. PBR 是一个总称，涵盖各种领域，例如基于物理的阴影、相机和灯光.
基于物理的着色 (PBS) 是 PBR 的关键组件，在 Wolfram 语言中作为 MaterialShading 实现. 本文档的其余部分将介绍它的实现及其背后的基本理论.
动机
基于物理的渲染技术现在在 3D 图形程序中很常见. 与纯艺术技巧相比，这些技术有一些关键优势，包括：
1. 物理精度 — 由于 PBR 技术更接近真实光学行为，利用该技术的管道能够实现更逼真的渲染.
2. 直观参数化 — PBR 着色器中的参数基于物理属性，而不是纯粹的美学值. 这使得调整参数以匹配真实世界的材料变得轻松. 也使得创造物理上不可能实现的材料变得更加困难.
3. 可移植性 — 大多数现代图形程序都支持 PBR 材料，并且其执行在不同的程序中往往是相似的. 因此，人们经常可以将一种材料的参数从一个渲染程序复制到另一个渲染程序并获得类似的结果.
物理正确性
几乎所有的渲染实现都是基于物理的. PBR 技术类别的区别在于它们遵循一组属性和规律. 包括：
4. 菲涅耳方程 — 光在介质界面处的反射和折射遵循菲涅耳方程.
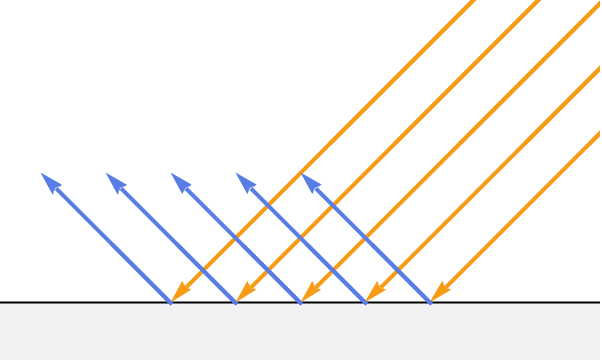
5. 亥姆霍兹互易 — 光线沿着相同的路径时，无论其方向如何，其行为都相同. 这使我们能够准确地“追踪”来自观察者的光线至它们的来源.
局限性
PBR 技术使用几何光学（也称为射线光学）模拟光，将光作为单独的射线建模. 该模型假设光线沿直线路径传播，在不同介质的界面处反射或折射除外.
• 相对论多普勒效应— 高速移动的物体可以改变从其表面反射的光波的频率.
渲染简介
PBS 的核心问题是如何确定离开物体表面的光的数量和方向. 为了理解这个问题的重要性，本节接下来将解释如何使用该信息来渲染场景.
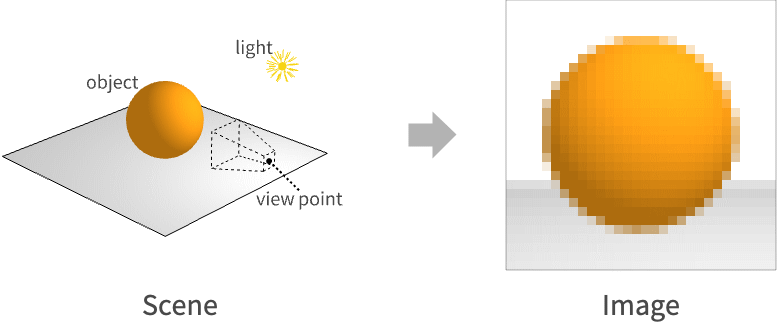
在三维计算机图形学中，渲染是将三维场景的数学表示转换为二维图像的过程. 这个图像由像素的矩形网格组成，其颜色是单独计算的. 计算像素颜色的过程称为着色.
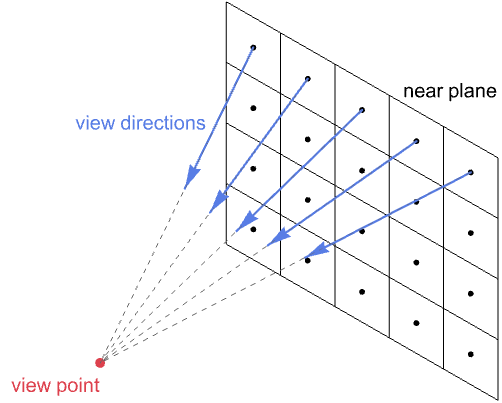
这些像素可以视为嵌入在视点前方小平面上的三维场景中. 这个平面被称为近平面（near plane）. 每个像素从它的中心到视点都有一个对应的视图方向向量.
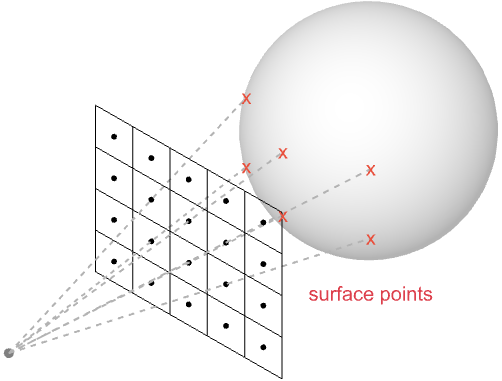
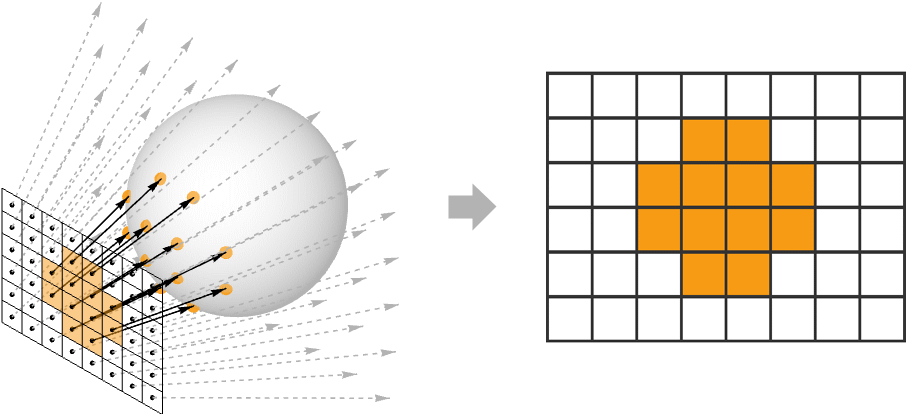
*像素的颜色由沿其视图方向穿过像素中心的入射光量决定. 进入像素的光必须来自场景中的物体表面，要么从表面直接发射，要么从其他光源反射. 由于我们的假设是光线沿直线传播，因此场景中每个像素至多有一个曲面点将光线引导至其中心并沿其观察方向.*
*注意：假设所有表面均不透明. 对于透明表面，可能需要考虑多个点.
有两种常用的方法来确定与给定像素对应的曲面点. 对于离线渲染，通常使用光线追踪从像素中心沿其负视图方向投射光线. 如果它与曲面相交，则相应的击中点就是希望的曲面点.
对于实时渲染，最常用的技术是通过对场景几何体应用一系列线性变换，将所有表面投影到近平面上. 接下来是光栅化和插值步骤，以确定每个像素的确切曲面点.
一旦知道曲面点，像素的颜色就由沿像素观察方向从该点发出的光量给出. 该出射光的量由反射率方程确定.
反射方程
场景中光的全局分布由渲染方程描述. 出于 PBR 的目的，使用了该方程的局部变体，称为反射方程.
该方程描述了从表面 
上的点向特定方向 
的出射光量. 这个光量称为该点的辐射亮度（radiance）.
此辐射亮度是一个光谱量，这意味着它由各种不同波长（即颜色）的光组成. 在测量真实世界的光源时，通常使用光谱功率分布 (SPD) 来描述这种辐射. 该 SPD 给出了整个可见光谱范围内的光强度.
在这些分布上存储和执行计算从计算角度说是昂贵的. 相反，图形程序将辐射存储为三维矢量，其通道表示光的红色、绿色和蓝色波长的强度. 由于人类感知颜色的方式，这三种波长的光可以组合形成大部分可见光谱.
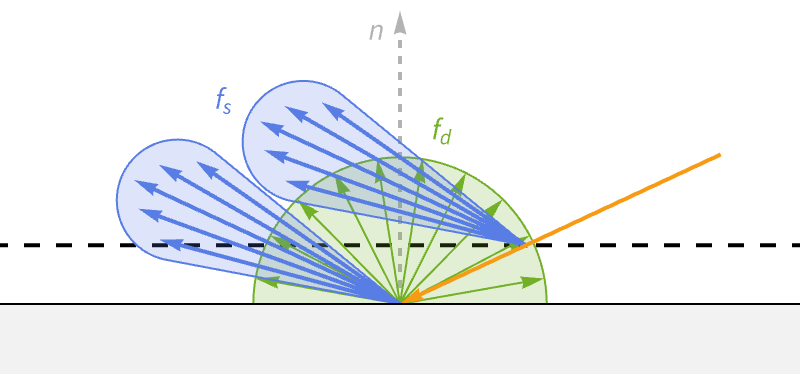
查看反射率方程，它表明出射光的辐射亮度是表面发出的光和反射的光的总和. 以下部分将详细介绍光的这两个贡献.
发射光（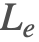
）
发射光是从表面自身产生的光. 在现实生活中，这通常是黑体辐射的结果，它会导致热物体发光.
在大多数图形程序中，此光由用户以 RGB 颜色的形式直接指定. 因此，确定发射光的量是很简单的，因为只需返回指定的颜色即可.
在 Wolfram 语言的默认照明系统中，发射光由 Glow 指定. 对于 MaterialShading，使用 "EmissionColor" 参数.
反射光（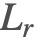
）
反射光包括从场景中的其他地方入射到曲面点上然后在出射方向上重新定向的所有光. 光的这种贡献使我们能够看到大多数物体，因为它们通常太冷而无法在人类可见光谱内发射黑体辐射.
积分来自这样一个事实，即我们必须考虑给定曲面点的所有可能的入射光方向. 所有这些可能方向的集合可以方便地通过与此时表面法线对齐的单位半球来描述. 该半球外的任何方向都来自表面后方，因此不会影响不透明材料的辐射.
不幸的是，这个积分无法对任意场景进行解析求解. 相反，积分必须在数值上近似，或者必须做出额外的假设来简化它.
对于使用光线追踪的离线渲染，常见的数值近似是在半球上执行蒙特卡罗采样. 这之后可能是去噪阶段以清理最终图像. 可以使用进一步优化（如重要性采样等）来减少所需的样本数量.
实时应用程序通常会对光源做出简化假设，从而可以对积分进行解析求解. 这种假设是入射到表面的光只能来自特殊光源，而不能来自场景中的其他表面. 这些特殊的光源被称为解析光. 三种常见的解析光类型是平行光（directional light）、定点光（point light）和聚光（spot light）.
通过仅使用解析光源，可以将半球上的积分转换为场景中所有光的总和.
现在由于我们有一个计算上可行的反射光公式，我们可以涵盖其总和中包含的三个项. 接下来的各节将详细介绍这些项； 下面只是简要说明：
入射光（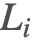
）
入射光项提供从给定光到特定曲面点的辐射亮度. 由于能量守恒，该项表示可以从该光源表面反射的最大辐射亮度.
解析光的辐射亮度取决于其类型. 在 Wolfram 语言中，每种光的辐射亮度定义如下：
下面的例子显示一个正方形被各类型的白色顶灯照亮. 定点光和聚光存在的衰减作用应该很明显.
有关照明规格和计算的更多信息，请参阅 Lighting.
朗伯余弦定律（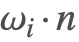
）
入射方向（
）和表面法线（
）之间的点积根据朗伯余弦定律对入射光的辐射亮度进行衰减.
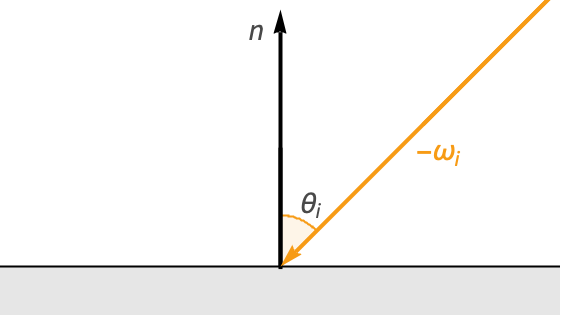
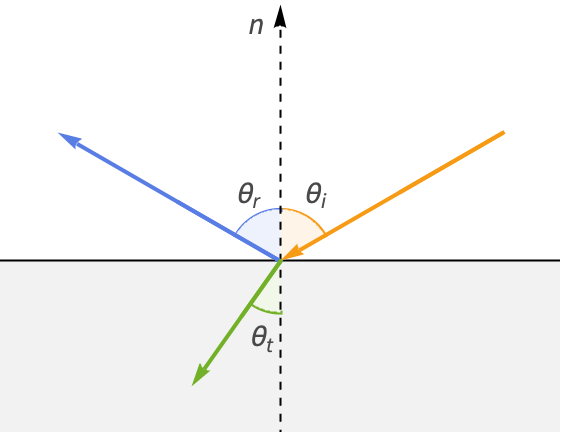
当光照射到表面时，它相对于表面法线所成的角度称为入射角（
）.
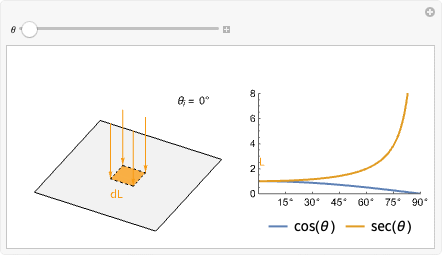
根据朗伯余弦定律，该入射光在该点处的漫射辐射亮度与入射角的余弦（
）成正比.
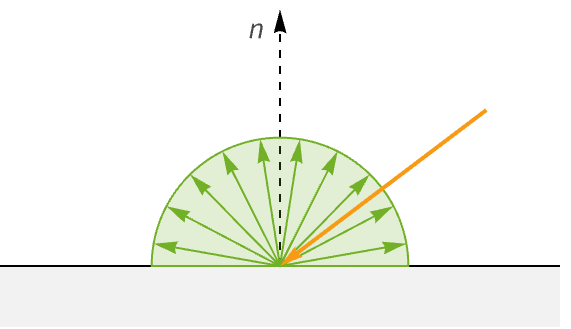
要理解底层原因，请想象物体表面上的一个小二维补丁. 如果一束光束垂直于表面（
）射向这个补丁，那么该光束的所有辐射亮度都会击中补丁. 然而，随着入射角的增加，光束的投影面积也增加，延伸到补丁区域之外。 这会导致光的辐射亮度散布在整个表面，这意味着这个小补丁整体接收的辐射亮度变少.
如果我们假想的小补丁是一个单位正方形，那么投影面积将等于 
. 这意味着原始补丁接收到的辐射亮度为 
.
注意，当入射角达到 90° 时，光束将平行于表面，因此我们的补丁将不会收到辐射亮度而保持黑暗.
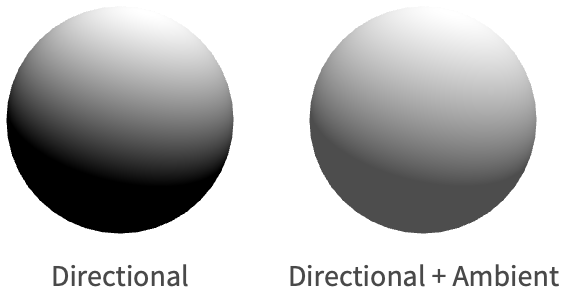
朗伯余弦定律适用于熟悉的哑光表面着色，甚至在非 PBR 实现中也很常见. 例如，以下球体上的照明仅使用朗伯余弦定律和来自上方的单个定向光源进行计算.
在实际应用中，入射角的余弦是通过取入射方向和表面法线的点积来计算的. 只要两个向量都被归一化，这两个操作是等效的. 这正是有时用余弦项代替反射光方程的原因.
双向反射分布函数（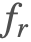
）
反射光的最后一项是双向反射分布函数（BRDF）. BRDF 决定表面点处的入射光重定向到出射方向上的比率. 与之前的项相比，此函数对于不同的材料类型是唯一的.
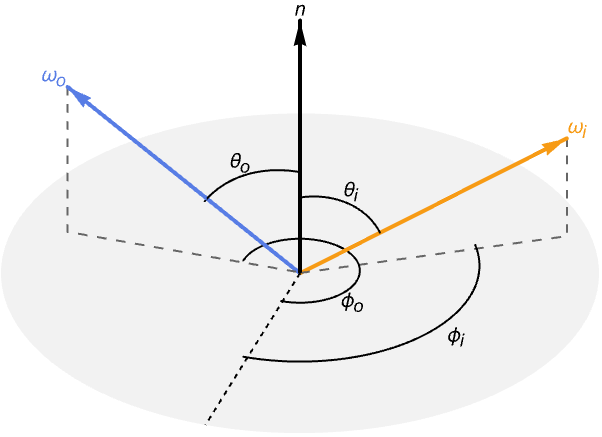
BRDF 是三个向量的函数：入射方向（
），出射方向（
）和表面法线（
）. 表面法线通常被省略，在这种情况下，这意味着法线位于 
轴的正方向.
还存在使用入射和出射方向相对于表面法线的方位角（
）和高度角（
）的等效参数化.
使用特殊设备，可以直接测量实际材料的 BRDF. 一个值得注意的例子是 Mitsubishi [1] 所做的分析. 下面显示了他们测量的一块 PVC 的 BRDF. 对于可视化，入射方向保持不变，而出射方向变化，以覆盖整个半球. 叶瓣的大小和颜色表示在该方向反射的光量.
对于大多数渲染器来说，直接使用实测的 BRDF 数据是不切实际的. 部分原因包括：
2. 渲染需要大量数据，使得 GPU 上的实时计算存在问题.
3. 每个测得的 BRDF 都对被测材料具有高度的特异性，不能轻易修改.
因此，图形程序选择使用可以近似各种材料的参数化 BRDF. 然后可以将测量数据用作基准，以与各种参数 BRDF 模型进行比较. 一旦找到合适的参数化，设计者就可以轻松调整参数以获得所需材料的外观.
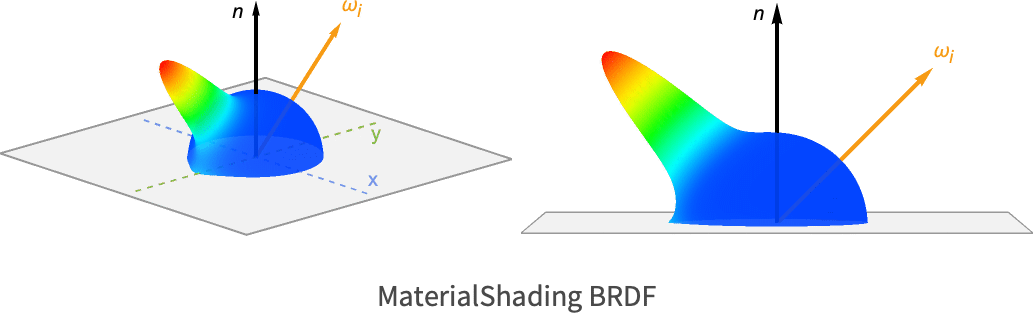
MaterialShading 使用的完整参数化 BRDF 的一个特定实例如下所示：
两种 BRDF
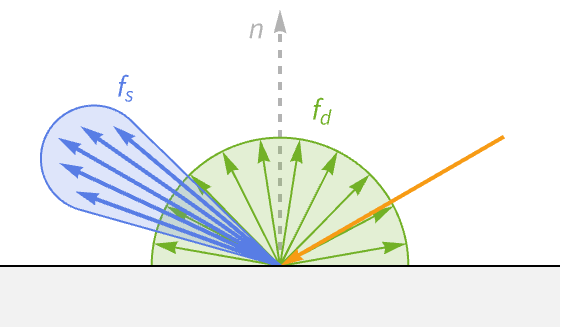
在实践中，图形程序不是使用一个而是两个单独的参数化 BRDF，两者相加以创建材料的完整 BRDF. 这些被称为镜面反射和漫反射 BRDF，它们代表光撞击表面时的两种不同行为——折射和反射.
反射光在理想的反射方向从表面反射. 同时，折射光以一定的倾斜角进入表面，该倾斜角由它离开介质的折射率（IOR）和进入介质的折射率（IOR）决定.
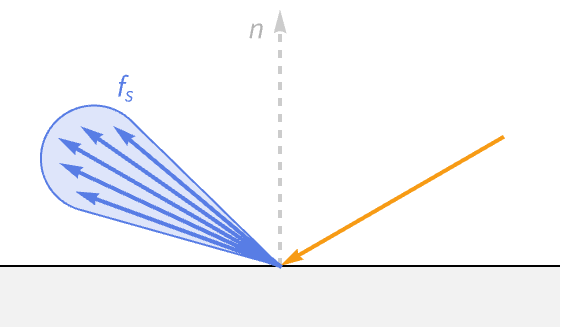
反射光
反射光从表面反射出来，就像一面完美的镜子，遵循理想的反射方向. 这种光被称为镜面光，基于拉丁词 speculum，意思是镜子. 镜面光是在光滑物体上看到明亮高光的原因. 在朝向观察者的角度与反射角度对齐的地方，高光是可见的. 因此，镜面光取决于观察者的方向.
折射光
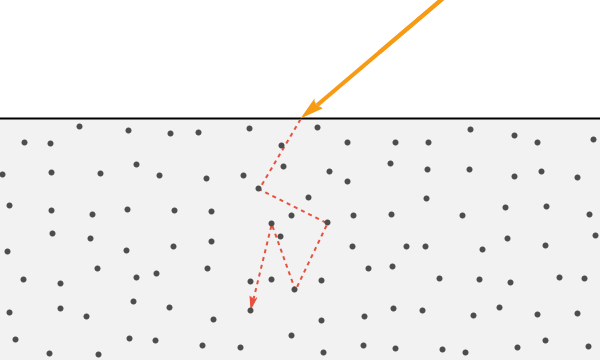
折射光的路径比较复杂. 进入表面后，它继续与材料中的粒子相互作用. 每次相互作用都会导致它进一步散射并损失能量. 如果光线失去所有能量，则认为它被材料吸收（即转化为热量）.
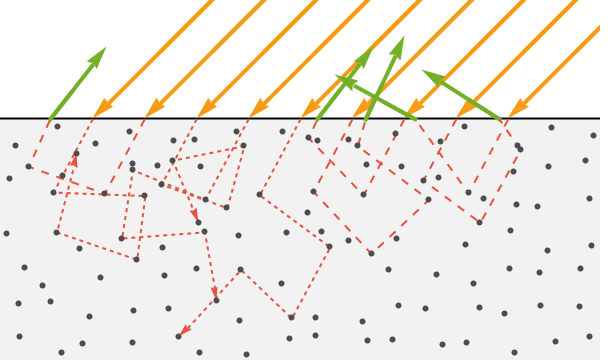
然而，一些散射光会设法逃离表面. 经历了许多次散射后，这种光的方向实际上是随机的.
如果有大量这样逃逸的光线，它们总体看起来在所有方向上是均匀散布的. 因此，这种光被称为漫反射光.
对于大多数不透明材料，折射光可穿透表面下方不到几纳米. 这也意味着离开表面的部分在其入口点附近（即在像素宽度内）. 因此，图形程序通常假设漫反射光从入口点发出.
对于像皮肤这样的半透明材料，折射光会穿透得更深，离开表面的点与进入点距离较远. 这种效果被称为次表面散射，需要额外的技术才能实现. 类似地，玻璃等透明材料在从物体背面射出之前以最小的吸收传输折射光. 这种效果称为传输，也需要额外的技术才能实现.
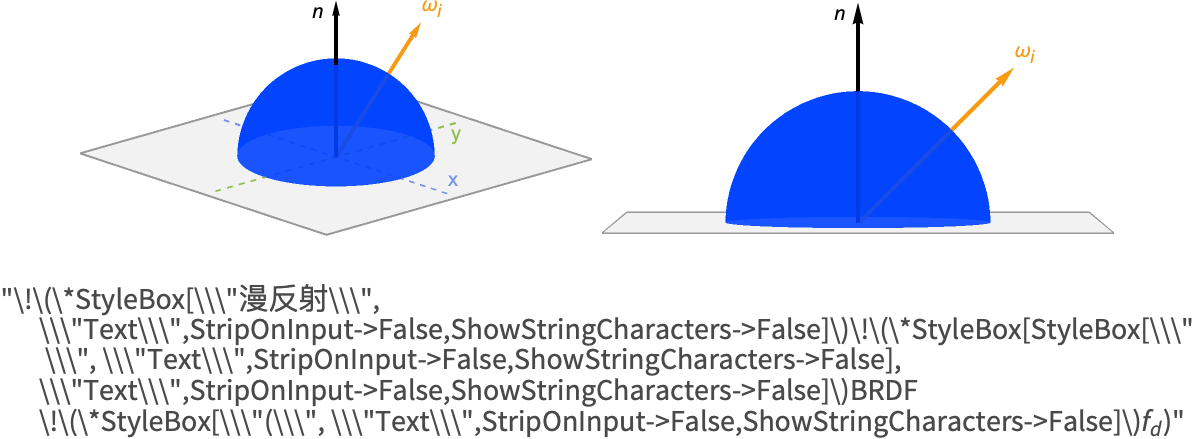
漫反射 BRDF
漫反射 BRDF 用于对光的折射部分进行建模，这些光会在靠近进入点的位置离开表面.
朗伯 BRDF 是漫反射 BRDF 的常见选择，由 MaterialShading 实现. 它被定义为：
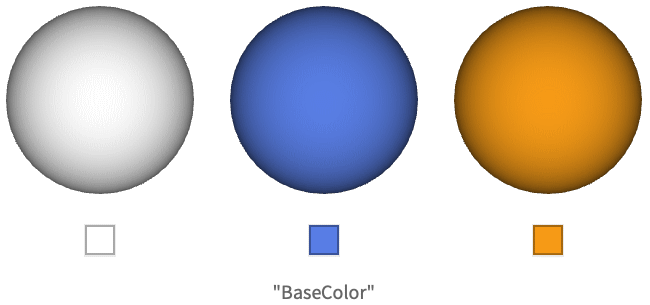
在计算机图形学的语境中，当被垂直于表面的单位辐射度的入射光照亮时，反照率颜色给出了从表面反射的漫射光的颜色. 换句话说，它没有应用任何照明的表面的颜色. 请注意，按 
缩放是为了能量守恒.
由这个 BRDF 形成的漫射瓣只是一个半球，因为它的值不依赖于观察者或光源的位置.
对于 MaterialShading，反照率颜色由 "BaseColor" 参数指定.
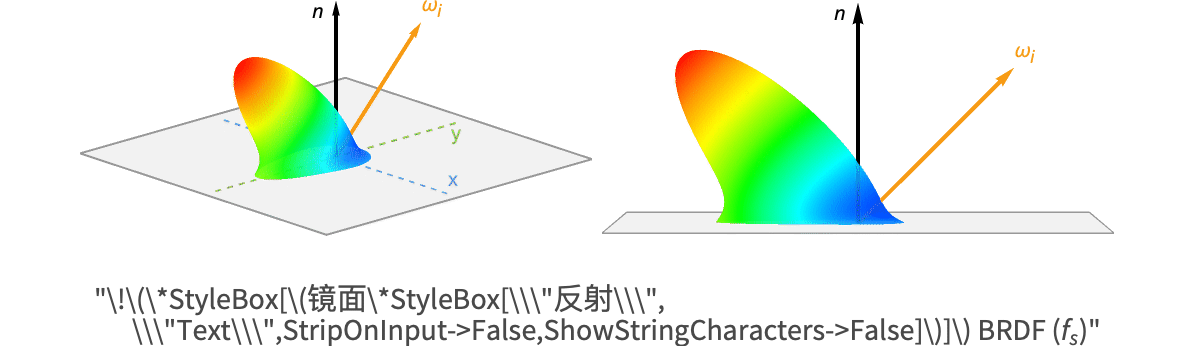
镜面反射 BRDF
与漫反射 BRDF 相比，镜面反射 BRDF 有点复杂，在深入研究最终方程之前需要了解一些理论.
根据定义，镜面光是在理想反射方向上从表面反射的光. 然而，如果真是这样，那么像球体这样的光滑物体上的高光将只存在于视图方向和入射方向对齐的单个无穷小点处. 但对于真实世界的材料而言，情况并非如此，它可以覆盖对象表面合理部分的光泽高光.
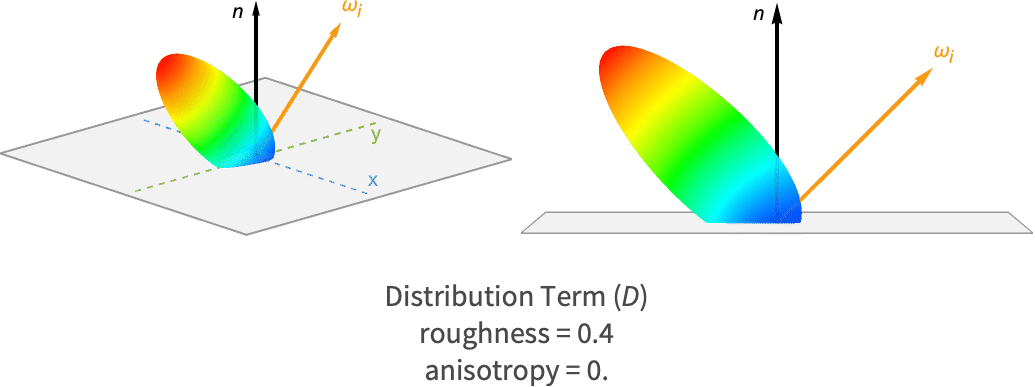
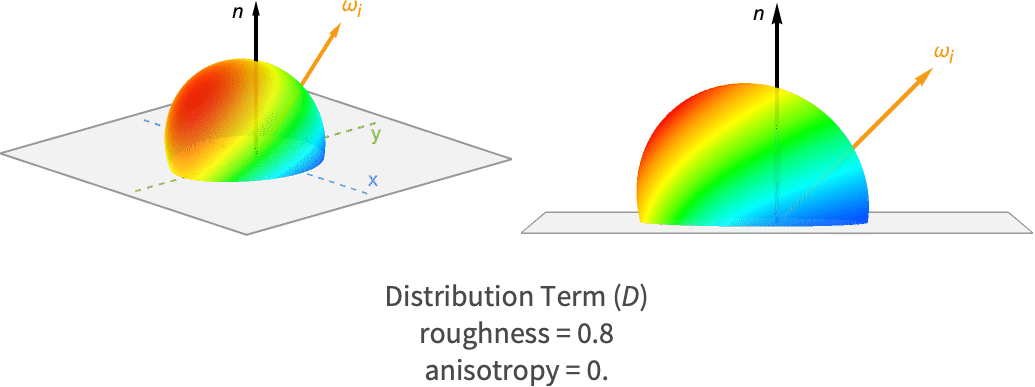
微面理论
微面理论适应于几乎所有镜面反射 BRDF. 该理论表明，虽然表面在宏观层面可能看起来很光滑，但在微观层面则由大量微面组成. 每个微面均是光学上的平面，这意味着当微面被一束光击中时，将以理想的反射方向反射光.
因此，镜面反射的变化是由这些微面方向的变化引起的. 这解释了为什么在宏观层面看起来光滑的表面仍可以返回一个关于理想反射方向变化的镜面波瓣.
在 PBR 实现中，漫反射 BRDF 的选择几乎是一致的，而镜面反射 BRDF 却有多种选项可供选择. 但是，由于每个版本都遵循微面理论，因此都遵循以下所示的相同结构.
该结构包含三个项，描述光如何与微平面相互作用. 各项的选择取决于图形程序，其中通常需要在物理精度和性能之间进行权衡.
• 菲涅耳项 — 被反射（因此没有被折射）的入射光的百分比.
在深入研究各项之前，我们必须首先介绍一下与微面相关的粗糙度和各向异性的概念.
粗糙度
分布项 (
) 和几何项 (
) 都需要一个参数 
来描述表面的粗糙度. 在微面级别，这种粗糙度对应于微面方向的变化. 请注意，在描述微面的方向时，我们实际上描述的是其表面法线的方向.
微面法线的变化越大，光越分散. 当 
时，所有微面法线都与宏观表面法线对齐，从而产生完美的镜面反射. 当 
接近 1 时，微面法线几乎是随机定向的，这导致反射光在本质上更接近漫反射.
通常不直接指定此 
项，而是将粗糙度参数作为输入，并将其重新映射到 
，以使粗糙度在感知上呈线性.
该粗糙度参数对应于 MaterialShading 的 "RoughnessCoefficient" 参数.
各向异性
图形程序通常假设所有材料都是各向同性的，这意味着无论从哪个角度看，它们反射的光都相同. 在微表面级别，这意味着微面法线的方向不会显示出对任何特定方向的偏好.
然而，一些现实世界的材料确实表现出对某一个方向反射光的强烈偏好. 这些材料称为各向异性材料，包括拉丝金属和木材等材料.
这种效果在镜面反射 BRDF 中通过考虑 
的两个值来实现，一个沿切线方向，一个沿双切线方向. 这两个值分别由 
和 
表示.
与 
值一样，用户不直接指定 
和 
，而是传递一个名为 anisotropy （各向异性）的属性，该属性与粗糙度一起用于计算各向异性的 
值.
在 MaterialShading 中，镜面反射的各向异性由 "SpecularAnisotropyCoefficient" 参数控制.
默认情况下，切线方向相对于观察者是水平的. 这个方向可以通过指定一个角度以及 "SpecularAnisotropyCoefficient" 属性来调整.
有了粗糙度和各向异性的知识，我们终于可以深入研究镜面反射 BRDF 的第一项了.
(
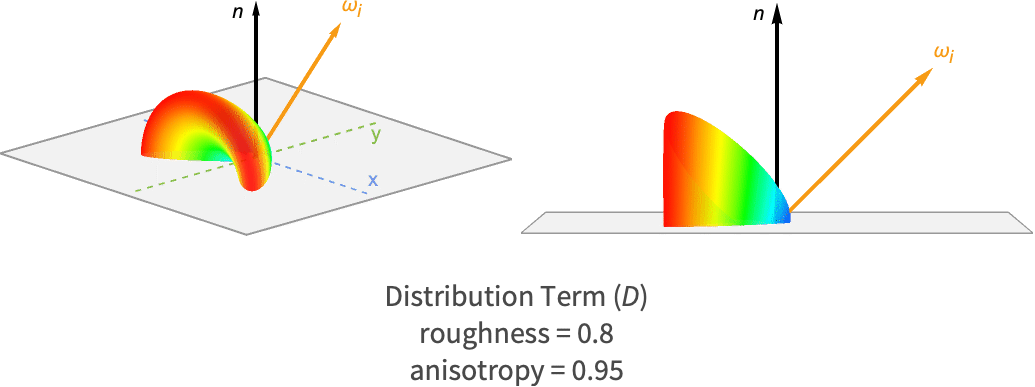
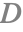) 分布项
正如我们在前面几节中看到的，镜面光总是在理想的反射方向上反射（
）. 因此，为了确定在特定方向上从表面反射的光量，必须首先确定以在该方向反射光的方式定向的微面的比率.
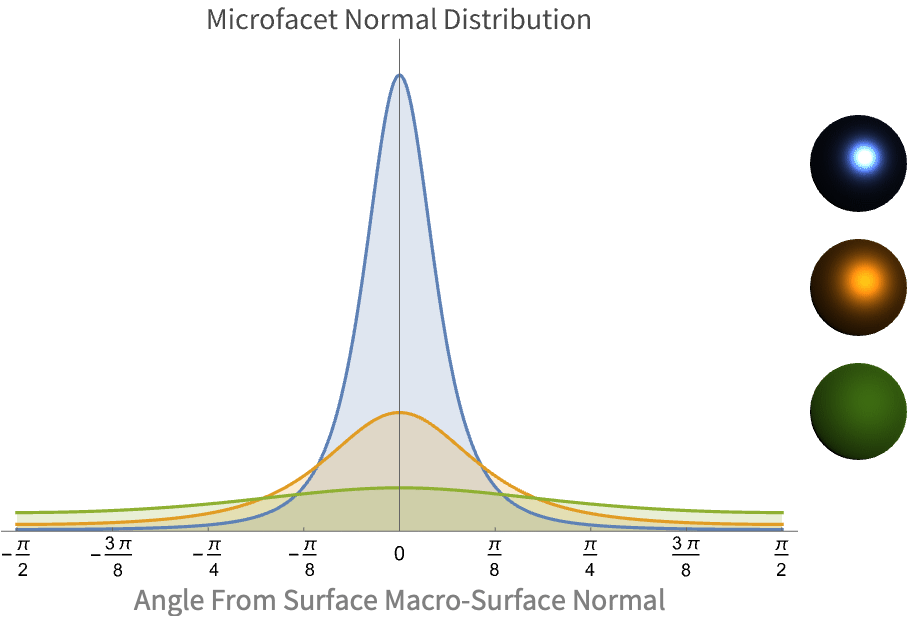
这由分布项给出，它描述微面法线相对于宏观表面法线的分布方式. 该项也称为正态分布函数（NDF）.
请注意有多少微面法线集中在宏观表面法线周围（图中为 0）. 对于光滑材料（蓝色），随着角度的增加，浓度会迅速下降. 同时，较粗糙的材料（绿色）显示出更均匀的微面法线浓度，暗示了它们的漫反射性质.
镜面反射 BRDF 从这个分布中采样一个特定的角度，成为分布项. 这是宏观表面法线与微面法线方向之间的角度，微面会将光从入射方向反射到出射方向. 根据反射定律，该法线方向必须位于入射方向和出射方向的中间. 因此，它通常被称为中间向量，计算如下：
对于各向异性材料，分布项必须考虑该中间向量如何与切线和双切线方向对齐，因为对于各向异性材料，粗糙度将根据这些方向而变化.
用于 MaterialShading 的分布项为 Burley [2]，这与华特迪士尼动画工作室使用的公式相同. 它被定义为：
(
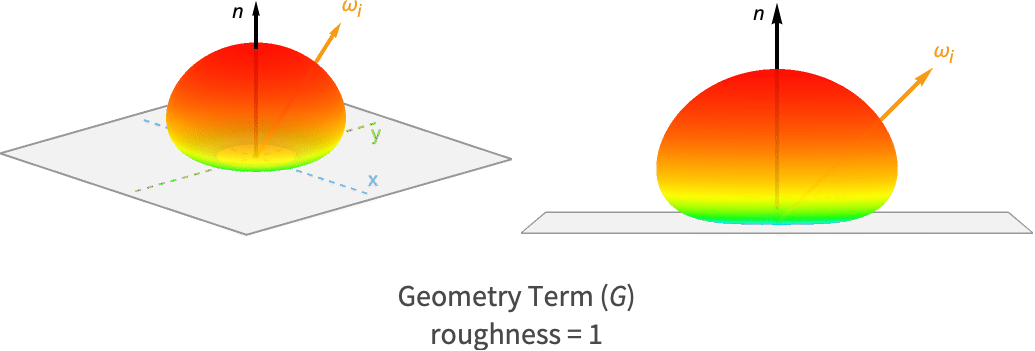
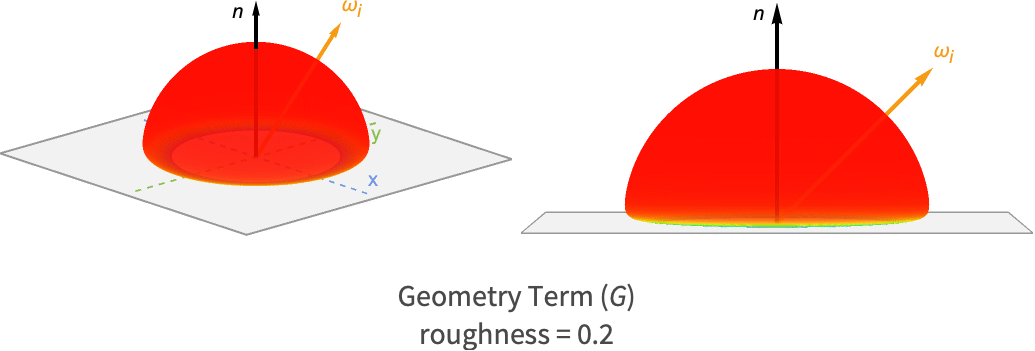
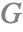) 几何项
几何项考虑了被其他微面遮蔽或掩蔽从而对最终反射光没有贡献的微面.
当微面朝向光源的路径被另一个微面阻挡时，微面就会被遮蔽（shadowing）. 类似地，当一个微面被另一个微面遮挡时，该微面对观察者不可见，这时就发生了掩蔽（masking）.
对于其几何项，MaterialShading 使用 GGX–Smith 高度相关的遮蔽和掩蔽函数 [3]:
注意：该项不受各向异性的影响. 如果材料是各向异性的，则取两个 
的平均值以获得该方程的单个 
值.
对于粗糙和光滑的表面，镜面反射 BRDF 的这个分量的波瓣如下所示.
请注意与光滑表面相比，较粗糙的表面如何在掠射角处产生较小的值. 这是有道理的，因为零方差的微面不会产生遮蔽或阴影，而高方差的微面更有可能在低角度遮挡其他微面.
(
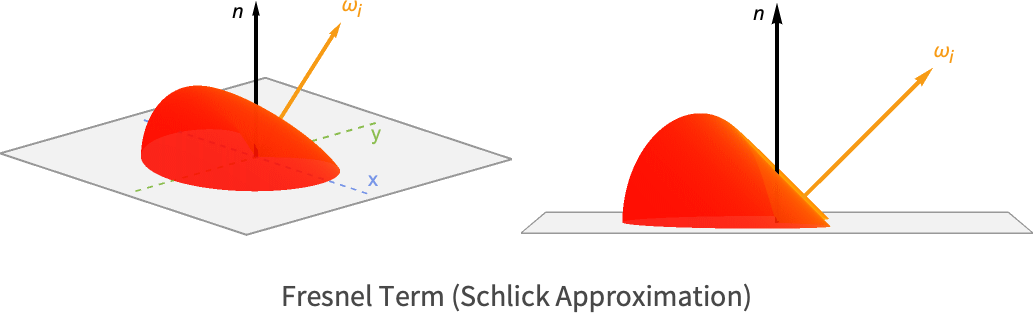
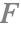) 菲涅耳项
在本文档的前面部分，我们介绍了光从一种介质穿过另一种介质时如何分成两个分量—折射和反射. 然而，光并不总是均匀地分成这两个分量.
菲涅耳方程描述了多少入射光被反射而不是被折射. 该比率由两种介质的入射角和折射率决定. 出于渲染的目的，这些介质通常是空气和相关物体的材质.
菲涅耳方程假设光入射在光学平面上. 因此，它单独适用于每个微面（与分布项和几何项不同，它们对微面做一些统计分布假设）.
在实践中，通常使用这些方程的近似版本，称为 Schlick 近似.
这里 
表示法向入射（光线垂直于表面）的镜面反射率. 同时，
是掠射角处的镜面反射率.
实际上，所有材料在掠射角的镜面反射率为 1.0. 这种行为称为菲涅耳效应，在观察大型平坦表面（例如大片静水）时尤为明显.
对于特别暗的材料，Schlick 近似的波瓣如下所示. 注意反射率在掠射角是如何增加的.
一种复杂情况是材料的折射率（IOR）会根据光的波长（即颜色）而变化. 因此，每个 RGB 颜色通道的 
需要单独计算.
MaterialShading 对介电（非金属）材料使用 Schlick 近似. 值 
由 "SpecularColor" 属性控制. 对于真实世界的介电材料，此值非常低，所有三 (3) 个颜色通道的值都约为 0.04.
用于金属材料的近似更复杂. 在讨论之前，我们将简要介绍计算机图形学中金属和非金属之间的区别.
导体与电介质
基于物理的着色模型通常遵循金属工作流程，它区分金属材料（导体）和非金属材料（电介质）. 漫射光和镜面反射光在这两种材料类型之间的表现显著不同，因此需要进行不同的计算.
电介质（非金属）
电介质是最常见的材料类型，包括塑料、石头、木材和皮革等. 这些材料将反射光而不改变其颜色. 然而，当光线被折射时，某些波长被吸收，而其余的则被发射，从而改变光的颜色. 这种漫射光的改变赋予这些材料我们熟悉的颜色. 例如，我们认为香蕉是黄色的，因为它们往往会吸收其他波长的光，只留下黄光作为它们的漫射颜色.
导体（金属）
所有金属均是导体，如金、铜、钢和青铜等. 这些材料具有吸收所有折射光的独特特性. 因此，它们没有漫反射颜色. 同时，它们仍然反射光，尽管它们改变了光的颜色. 金属如何改变这种反射光将决定我们感知到的金属的颜色. 例如，金使白光呈现黄色，而铜呈现出淡红色. 如果金属对所有波长的反射大致相同，则会显示为某种灰色阴影，例如铁和铝.
(
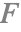) 导体的菲涅耳项
Schlick 近似对于电介质材料很有用，其中镜面反射高光对最终外观有很小的贡献. 然而，对于导体（即金属），镜面反射分量构成了它们的整体外观. 因此，对这些材料使用更精确的近似值是有利的.
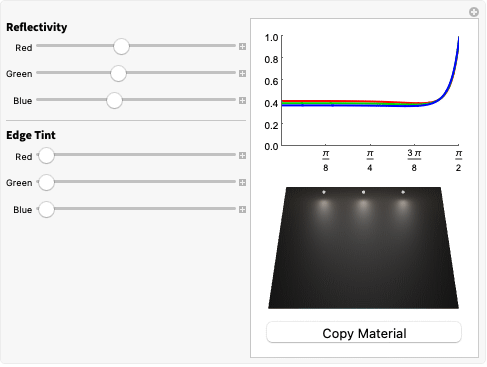
MaterialShading 使用 Sébastien Lagarde [4] 描述的介电导体菲涅耳公式. 他的公式依赖于 IOR 和消光系数来近似材料的反射率曲线.
但是，在尝试对视觉参考中的材质进行匹配时，直接为每个 RGB 通道设置这些属性的值并不直观. 因此，MaterialShading 还使用了一个中间层，该层根据反射率颜色和边缘色调计算 IOR 和消光系数. 反射率颜色描述大部分表面的镜面反射颜色，而边缘色调决定掠射角（通常在物体边缘）的光线色调.
MaterialShading 使用 Gulbrandsen [5] 描述的反射率和边缘色调映射.
下面的示例显示了红色、绿色和蓝色波长的光的反射率，由这些反射率和边缘色调参数控制. 请注意，增加特定波长的边缘色调会导致该颜色在掠射角更加突出.
对于 MaterialShading，金属材料的反射率和边缘色调分别由 "BaseColor" 和 "SpecularColor" 参数设置.
附加效果
到此为止，我们所看到的参数化 BRDF 可以很好地近似具有单个不透明层的材料. 然而，我们可以进行一些修改，以使它能够近似更多的材料类型.
涂层
在某些材料基础表面覆盖一层薄薄的透明涂层是很常见的. 对于汽车油漆和成品木材，这种涂层通常由漆（lacquer）或聚氨酯（polyurethane）制成. 由于额外的反射，这种涂层使表面看起来更光亮.
在 PBS 中，这种效果是通过假设在基础表面正上方存在次要镜面反射层来实现的. 现在我们将两次分离入射光，一次在涂层，一次在基础表面.
因为涂层被假定为非金属材质，涂层的镜面反射分量使用介电镜面反射 BRDF. 与基础层不同，穿过涂层的光不会形成漫反射波瓣，而是传播到基础表面并被基础表面的镜面反射和漫反射 BRDF 使用.
在 MaterialShading 中，涂层可以使用 "CoatColor" 参数指定. 当一个涂层被指定后，可以使用附加属性 "CoatRoughnessCoefficient" 和 "CoatAnisotropyCoefficient"，它们对应于基础表面的 "RoughnessCoefficient" 和 "SpecularAnisotropyCoefficient" 属性.
光泽
一些织物由许多垂直于宏观表面的纤维组成. 在掠射角，这些纤维的边缘倾向于与出射方向对齐并导致反向散射. 这会在材料边缘（如天鹅绒等）创建高光.
这种效果是使用额外的 BRDF 实现的，其分布项适合这类材料. MaterialShading 使用 Sony Pictures [6] 描述的光泽 BRDF：
在 MaterialShading 中，光泽可以使用 "SheenColor" 属性指定. 当指定了光泽颜色时，附加属性 "SheenRoughnessCoefficient" 可用于确定光泽照明的粗糙度.
环境照明
到目前为止，我们只讨论了三种解析照明——平行光、定点光和聚光. 这些有时也称为直接光，因为它们将光直接从光源投射到表面.
然而，在现实世界中，大量入射在表面上的光是间接光. 这是在到达当前表面之前被一个或多个其他表面反射的光. 模拟这种间接光的过程称为全局照明（GI），并且有多种方法可以用来实现它.
对于实时渲染器，一种廉价而有效的方法是使用环境项. 该项被添加到反射方程的结果出射辐射亮度中，以近似来自所有方向的恒定入射辐射亮度. 在 Wolfram 语言中，该项通过指定 "Ambient" 光来设置.
默认系统外观和 MaterialShading 都支持环境光. 但 MaterialShading 还允许用户设置表面的环境光遮蔽.
环境光遮蔽是指物体的角落和缝隙由于不像表面的其余部分那样接收到那么多的间接光，而往往更暗的现象. 对于 MaterialShading，可以使用 "AmbientExposureFraction" 参数设置暴露在材质表面的环境光的比例. 但是该参数通常仅与纹理一起使用，以将材料的裂缝准确地映射到物体的表面.
References
1. Ngan, A., F. Durando and W. Matusik. Experimental Analysis of BRDF Models. The Eurographics Association (2005).
2. Burley, B. Physically-Based Shading at Disney. Walt Disney Animation Studios (2012).
3. Heitz, E. "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs." Journal of Computer Graphics Techniques, Williams College (2014).
4. Lagarde, S. Memo on Fresnel Equations. 2013. https://seblagarde.wordpress.com/2013/04/29/memo-on-fresnel-equations.
5. Gulbrandsen, O. "Artist Friendly Metallic Fresnel." Journal of Computer Graphics Techniques (JCGT) 3, no. 4 (2014): 64–72.
6. Estevez, A. and C. Kulla. Production Friendly Microfacet Sheen BRDF. Sony Pictures Imageworks (2017).
7. Smythe, D. and J. Stone. MaterialX: An Open Standard for Network-Based CG Object Looks, Version 1.38, 2021.