ToUnorderedPairs[g]
constructs a list of unordered pairs representing the edges of graph ![]() . Each edge, directed or undirected, results in a pair in which the smaller vertex appears first.
. Each edge, directed or undirected, results in a pair in which the smaller vertex appears first.


ToUnorderedPairs
ToUnorderedPairs[g]
constructs a list of unordered pairs representing the edges of graph ![]() . Each edge, directed or undirected, results in a pair in which the smaller vertex appears first.
. Each edge, directed or undirected, results in a pair in which the smaller vertex appears first.
Details and Options
- ToUnorderedPairs functionality is now available in the built-in Wolfram Language function EdgeList.
- To use ToUnorderedPairs, you first need to load the Combinatorica Package using Needs["Combinatorica`"].
- An option called Type that takes on values All or Simple can be used, with All being the default value. Type->Simple ignores multiple edges and self-loops in
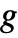 .
.
Tech Notes
Related Guides
-
▪
- Graph Construction and Representations ▪
- Graphs & Networks ▪
- Graph Visualization ▪
- Computation on Graphs ▪
- Graph Construction & Representation ▪
- Graphs and Matrices ▪
- Graph Properties & Measurements ▪
- Graph Operations and Modifications ▪
- Statistical Analysis ▪
- Social Network Analysis ▪
- Graph Properties ▪
- Mathematical Data Formats ▪
- Discrete Mathematics
Text
Wolfram Research (2012), ToUnorderedPairs, Wolfram Language function, https://reference.wolfram.com/language/Combinatorica/ref/ToUnorderedPairs.html.
CMS
Wolfram Language. 2012. "ToUnorderedPairs." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/Combinatorica/ref/ToUnorderedPairs.html.
APA
Wolfram Language. (2012). ToUnorderedPairs. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/Combinatorica/ref/ToUnorderedPairs.html
BibTeX
@misc{reference.wolfram_2025_tounorderedpairs, author="Wolfram Research", title="{ToUnorderedPairs}", year="2012", howpublished="\url{https://reference.wolfram.com/language/Combinatorica/ref/ToUnorderedPairs.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_tounorderedpairs, organization={Wolfram Research}, title={ToUnorderedPairs}, year={2012}, url={https://reference.wolfram.com/language/Combinatorica/ref/ToUnorderedPairs.html}, note=[Accessed: 11-March-2026]}