FEMDocumentation`
FEMDocumentation`

InitializeBoundaryConditions

InitializeBoundaryConditions[vd,sd,{{bc11,…},{bc21,…},…}]

initializes the system of boundary conditions beqni in accordance with variable data vd and solution data sd to generate a BoundaryConditionData object.

更多信息和选项

  • The boundary conditions bcij can either be DirichletCondition, NeumannValue or PeriodicBoundaryCondition.
  • The i^(th) set of boundary conditions bcij is associated with the i^(th) equation from:
  • The boundary conditions can be functions of space and time.
  • Variable data vd and solution data sd are corresponding lists of variables and values. Templates for vd and sd may be generated using NDSolve`VariableData and NDSolve`SolutionData, and components may be set using NDSolve`SetSolutionDataComponent.
  • InitializeBoundaryConditions verifies and optimizes the boundary conditions in accordance with variable data vd and solution data sd.
  • The "Space" component of vd and sd should be set to the spatial variables and the spatial mesh represented as a NumericalRegion object, respectively.
  • The "DependentVariables" component of vd should be set to the list of unknown function names without arguments.
  • For time-dependent problems, the "Time" component of vd and sd should be set to the temporal variable and the initial time, respectively.
  • For parametric problems, the "Parameters" component of vd and sd should be set to the parametric variables and the initial parametric values, respectively.
  • The following options can be given:
  • "BoundaryTolerance"Automatictolerance for boundary condition predicate
    "ScaleFactor"Automaticscaling factor for transient handling of Dirichlet boundary conditions
  • Setting the option from NDSolve and related functions is explained in NDSolve Finite Element Options.

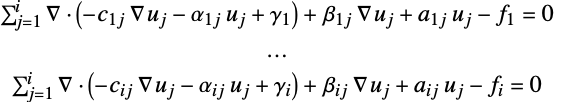
范例

打开所有单元关闭所有单元

基本范例  (1)

Load the finite element package:

Set up a NumericalRegion:

Set up variable and solution data:

Initialize a boundary condition:

Scope  (2)

Set up variable and solution data for a system of two equations:

Initialize the boundary conditions:

Initialize Dirichlet conditions for u and v for the first equation and a Dirichlet condition for v and a Neumann condition for the second equation:

Options  (1)

"BoundaryTolerance"  (1)

Initialize boundary conditions that are inconsistent:

During the boundary condition discretization stage, a warning will be issued if DirichletCondition boundary conditions are inconsistent:

The default "BoundaryTolerance" is Automatic and does not warn about inconsistent boundary conditions but will eliminate duplicate boundary conditions that may come up during the inconsistent boundary condition analysis. Setting "BoundaryTolerance" to Infinity will not perform any inconsistency check.

Wolfram Research (2014)，InitializeBoundaryConditions，Wolfram 语言函数，https://reference.wolfram.com/language/FEMDocumentation/ref/InitializeBoundaryConditions.html （更新于 2020 年）.

文本

Wolfram Research (2014)，InitializeBoundaryConditions，Wolfram 语言函数，https://reference.wolfram.com/language/FEMDocumentation/ref/InitializeBoundaryConditions.html （更新于 2020 年）.

CMS

Wolfram 语言. 2014. "InitializeBoundaryConditions." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/FEMDocumentation/ref/InitializeBoundaryConditions.html.

APA

Wolfram 语言. (2014). InitializeBoundaryConditions. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/FEMDocumentation/ref/InitializeBoundaryConditions.html 年

BibTeX

@misc{reference.wolfram_2024_initializeboundaryconditions, author="Wolfram Research", title="{InitializeBoundaryConditions}", year="2020", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/InitializeBoundaryConditions.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_initializeboundaryconditions, organization={Wolfram Research}, title={InitializeBoundaryConditions}, year={2020}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/InitializeBoundaryConditions.html}, note=[Accessed: 05-November-2024 ]}