InitializePDECoefficients[vd,sd,rules]
initializes the coefficients specified by rules in accordance with variable data vd and solution data sd to generate a PDECoefficientData object.


InitializePDECoefficients
InitializePDECoefficients[vd,sd,rules]
initializes the coefficients specified by rules in accordance with variable data vd and solution data sd to generate a PDECoefficientData object.
Details and Options
- The coefficients are assumed to come from a second-order system of
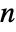 PDEs in
PDEs in 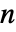 space dimensions of the form:
space dimensions of the form: - In InitializePDECoefficients[vd,sd,rules], the rules should be of the form name->coefficient. The possible coefficient names are:
-
"LoadCoefficients" {{f1},{f2},…} 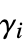 is a scalar
is a scalar"LoadDerivativeCoefficients" {{γ1},{γ2},…} 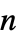 is a vector of length
is a vector of length 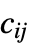
"DiffusionCoefficients" {{-c11,-c12,…},{-c21,-c22,…},…} 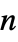 may be specified as scalars, diagonal vectors of length
may be specified as scalars, diagonal vectors of length 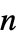 , or
, or 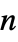 ×
×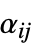 matrices
matrices"ConservativeConvectionCoefficients" {{-α11,-α12,…},{-α21,-α22,…},…} 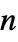 is a vector of length
is a vector of length 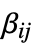
"ConvectionCoefficients" {{β11,β12,…},{β21,β22,…},…} 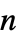 is a vector of length
is a vector of length 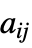
"ReactionCoefficients" {{a11,a12,…},{a21,a22,…},…} 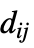 is a scalar
is a scalar - If a rule is not specified for any of these coefficient names, the coefficients of that type are all assumed to be 0.
- DiscretizePDE will take the generated PDECoefficientData object and provide system matrices such that
- where
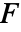 is the stiffness matrix and
is the stiffness matrix and 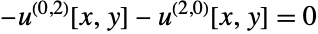 a load vector.
a load vector. - Transient systems of PDEs may be specified up through second, with
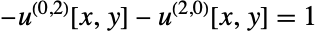 the first-order temporal derivative and
the first-order temporal derivative and 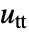 the second-order temporal derivative.
the second-order temporal derivative. - The transient coefficient form is:
- DiscretizePDE will take the generated PDECoefficientData object and provide system matrices such that
- where
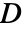 is the mass matrix,
is the mass matrix, 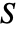 the damping matrix,
the damping matrix, 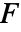 the stiffness matrix and
the stiffness matrix and 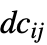 a load vector.
a load vector. - The possible damping coefficient names are:
-
"DampingDiffusionCoefficients" {{-dc11,-dc12,…},{-dc21,-dc22,…},…} 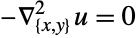 may be specified as scalars, diagonal vectors of length
may be specified as scalars, diagonal vectors of length 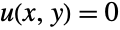 or
or 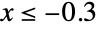 ×
×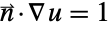 matrices
matrices"DampingConservativeConvectionCoefficients" {{-dα11,-dα12,…},{-dα21,-dα22,…},…} 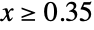 is a vector of length
is a vector of length 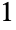
"DampingConvectionCoefficients" {{dβ11,dβ12,…},{dβ21,dβ22,…},…} 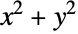 is a vector of length
is a vector of length 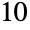
"DampingReactionCoefficients" {{dα11,dα12,…},{dα21,dα22,…},…} 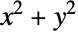 is a scalar
is a scalar - The possible mass coefficient names are:
-
"MassDiffusionCoefficients" {{-mc11,-mc12,…},{-mc21,-mc22,…},…} 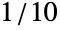 may be specified as scalars, diagonal vectors of length
may be specified as scalars, diagonal vectors of length 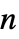 or
or 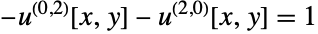 ×
×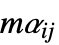 matrices
matrices"MassConservativeConvectionCoefficients" {{-mα11,-mα12,…},{-mα21,-mα22,…},…} 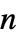 is a vector of length
is a vector of length 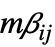
"MassConvectionCoefficients" {{mβ11,mβ12,…},{mβ21,mβ22,…},…} 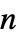 is a vector of length
is a vector of length 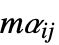
"MassReactionCoefficients" {{mα11,mα12,…},{mα21,mα22,…},…} 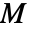 is a scalar
is a scalar - "Mass" coefficients contribute to the mass matrix
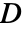 , "Damping" coefficients contribute to the damping matrix
, "Damping" coefficients contribute to the damping matrix 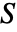 , and the remaining coefficients contribute to the stiffness matrix
, and the remaining coefficients contribute to the stiffness matrix 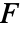 and the load vector
and the load vector 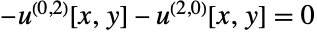 .
. - NDSolve reduces transient systems so that they are first order in time.
- The coefficients can be functions of space, time, parameters, dependent variables and first-order derivatives of dependent variables.
- Variable data vd and solution data sd are corresponding lists of variables and values. Templates for vd and sd may be generated using NDSolve`VariableData and NDSolve`SolutionData, and components may be set using NDSolve`SetSolutionDataComponent.
- InitializePDECoefficients verifies and optimizes the coefficients in accordance with variable data vd and solution data sd.
- The "Space" component of vd and sd should be set to the spatial variables and the spatial mesh represented as a NumericalRegion object, respectively.
- The "DependentVariables" component of vd should be a list of dependent variable name symbols without arguments.
- For time-dependent problems, the "Time" component of vd and sd should be set to the temporal variable and the initial time, respectively.
- For nonlinear problems, the "DependentVariables" component of sd should be set to the initial seedings for the dependent variables.
- For parametric problems, the "Parameters" component of vd and sd should be set to the parametric variables and the initial parametric values, respectively.
- InitializePDECoefficients has the following options:
-
"VerificationData" Automatic specify PDE coefficient verification data - Options given to InitializePDECoefficients can be given to NDSolve by specifying "InitializePDECoefficientsOptions". »
- Setting the option from NDSolve and related functions is explained in NDSolve Finite Element Options.
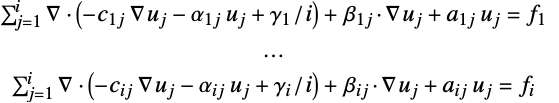
Examples
open all close allBasic Examples (2)
Load the finite element package:
Set up a NumericalRegion:
Set up variable and solution data:
Scope (6)
Coefficients can be functions:
Coefficients can be interpolation functions:
Coefficients can be nonlinear:
If the input for "DiffusionCoefficient" is a vector, it is interpreted as the diagonal of the requested input matrix:
If the input for "DiffusionCoefficient" is a scalar, the scalar is put in all places of the diagonal of the requested matrix:
Options (1)
"VerificationData" (1)
The PDE coefficients that are given to InitializePDECoefficients are verified so that they evaluate to numeric input:
The verification is done by finding a test coordinate that lies within the NumericalRegion. It may, however, happen that the automatically chosen test coordinate or test ElementMarker are at a singularity:
Overwriting the automatic finding of the verification data can be done with the "VerificationData" option:
Additionally, the automatic ElementMarker can be changed:
For nonlinear problems, the verification data for the dependents and the derivative of the dependents can be modified with "DependentVariables" and "DependentVariablesDerivative", respectively:

Change the test value for the dependent variable to be 1 and not 0 from the initial condition:
Change the test value of the derivative of the dependent variable to the vector {1,1}. The components of the vector are the values of the derivative in each space direction. Currently, a default 0.1 is used:
Applications (6)
Specify a Laplace equation ![]() over a disk with Dirichlet and Neumann conditions
over a disk with Dirichlet and Neumann conditions ![]() for
for ![]() and
and ![]() for
for ![]() :
:
Inspect the diffusion coefficients:
Discretize, solve, interpolate and visualize the solution:
The "LoadCoefficients" coefficient is used by NIntegrate to integrate over a region:
Use NIntegrate to verify the result:
A "ReactionCoefficients" of ![]() can be used to evaluate a function, for example,
can be used to evaluate a function, for example, ![]() over a region:
over a region:
Visualize the evaluated function:
A "ReactionCoefficients" of ![]() in combination with a "LoadCoefficients" can be used to scale a function, for example,
in combination with a "LoadCoefficients" can be used to scale a function, for example, ![]() over a region by a factor of
over a region by a factor of ![]() :
:
Visualize the scaled evaluated function:
A "ReactionCoefficients" in combination with a "LoadDerivativeCoefficients" can be used to interpolate the derivative of a function over a region:
Visualize the difference between the numerical approximation and the exact derivative:
Specify an equation with mixed spatial and temporal derivatives ![]() in the domain
in the domain ![]() :
:
Specify Dirichlet conditions ![]() ,
, ![]() and initial conditions
and initial conditions ![]() :
:
Set up the variable and solution data:
Initialize the boundary conditions:
Discretize the PDE coefficients. In this case, all PDE coefficients are time independent:
Discretize the boundary conditions:
Write a function to compute the residual of the PDE:
Evaluate the initial conditions:
Set up a function for the sparsity patterns of the system matrices:
Compute the sparsity patterns:
Create a unified interpolating function:
For comparison, compute a solution with the tensor product grid method:
Properties & Relations (2)
Options given to InitializePDECoefficients can be given to NDSolve by specifying "InitializePDECoefficientOptions":
Specify "VerificationData" to pass a coordinate that is not at a singularity:
Convert a Poisson equation ![]() into coefficients:
into coefficients:
Use GetInactivePDE to create an inactive version of the input:
Possible Issues (1)
Typically, NDSolve will detect if coefficients do not evaluate to numeric quantities with the correct dimensions and warn about that:
To verify that the coefficients given are adequate for each operator, the coefficients undergo a test evaluation using the initial point in time and a coordinate from the region. If the combination of the coefficient and the used values cancel out, NDSolve cannot detect if a coefficient has not been specified. NDSolve will then give a message that it was not able to compute the elements contributed by a specific operator:
In the preceding case, evaluating the load operator at t=0 and x=-π will let the load operator vanish, and NDSolve cannot detect that k has not been specified:
Tech Notes
Related Guides
Text
Wolfram Research (2014), InitializePDECoefficients, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDECoefficients.html (updated 2024).
CMS
Wolfram Language. 2014. "InitializePDECoefficients." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDECoefficients.html.
APA
Wolfram Language. (2014). InitializePDECoefficients. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDECoefficients.html
BibTeX
@misc{reference.wolfram_2025_initializepdecoefficients, author="Wolfram Research", title="{InitializePDECoefficients}", year="2024", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDECoefficients.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_initializepdecoefficients, organization={Wolfram Research}, title={InitializePDECoefficients}, year={2024}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDECoefficients.html}, note=[Accessed: 25-February-2026]}