InitializePDECoefficients
InitializePDECoefficients[vd,sd,rules]
変数データ vd と解データ sd に従った規則によって指定された係数を初期化し,PDECoefficientDataオブジェクトを生成する.
詳細とオプション
- 係数は,以下の形式の
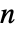 個の空間次数における
個の空間次数における 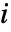 個の二階偏微分方程式の系からのものであると想定される.
個の二階偏微分方程式の系からのものであると想定される. - InitializePDECoefficients[vd,sd,rules]では,rules は name->coefficient の形式のものでなければならない.可能な係数名は以下の通りである.
-
"LoadCoefficients" {{f1},{f2},…} 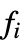 はスカラーである
はスカラーである"LoadDerivativeCoefficients" {{γ1},{γ2},…} 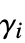 は長さ
は長さ 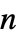 のベクトルである
のベクトルである"DiffusionCoefficients" {{-c11,-c12,…},{-c21,-c22,…},…} 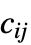 は,スカラー,長さ
は,スカラー,長さ 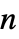 の対角ベクトル,
の対角ベクトル,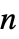 ×
×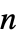 の行列のいずれかとして指定することができる
の行列のいずれかとして指定することができる"ConservativeConvectionCoefficients" {{-α11,-α12,…},{-α21,-α22,…},…} 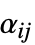 は長さ
は長さ 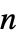 のベクトルである
のベクトルである"ConvectionCoefficients" {{β11,β12,…},{β21,β22,…},…} 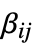 は長さ
は長さ 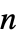 のベクトルである
のベクトルである"ReactionCoefficients" {{a11,a12,…},{a21,a22,…},…} 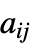 はスカラーである
はスカラーである - 規則がこれらの係数名について指定されていない場合には,そのタイプの係数はすべて0であると想定される.
- DiscretizePDEは一般化されたPDECoefficientDataオブジェクトを取り,以下のような系の行列を提供する.
- このとき
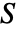 は剛性行列であり,
は剛性行列であり,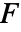 は荷重ベクトルである.
は荷重ベクトルである. - 偏微分方程式の定常系は
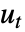 が一階の時間導関数,
が一階の時間導関数,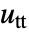 が二階の時間導関数として,二階まで指定することができる.
が二階の時間導関数として,二階まで指定することができる. - 定常係数形式は以下である.
- DiscretizePDEは一般化されたPDECoefficientDataオブジェクトを取り,以下のような系の行列を提供する.
- このとき
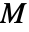 は質量行列,
は質量行列,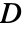 は減衰行列,
は減衰行列,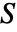 は剛性行列,
は剛性行列,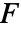 は荷重ベクトルである.
は荷重ベクトルである. - 可能な減衰係数名は以下の通りである.
-
"DampingDiffusionCoefficients" {{-dc11,-dc12,…},{-dc21,-dc22,…},…} 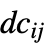 はスカラー,長さ
はスカラー,長さ 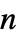 の対角ベクトル,
の対角ベクトル,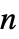 ×
×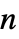 行列のいずれかとして指定できる.
行列のいずれかとして指定できる."DampingConservativeConvectionCoefficients" {{-dα11,-dα12,…},{-dα21,-dα22,…},…} 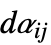 は長さ
は長さ 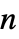 のベクトルである
のベクトルである"DampingConvectionCoefficients" {{dβ11,dβ12,…},{dβ21,dβ22,…},…} 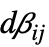 は長さ
は長さ 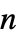 のベクトルである
のベクトルである"DampingReactionCoefficients" {{dα11,dα12,…},{dα21,dα22,…},…} 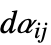 はスカラーである
はスカラーである - 可能な質量係数名は以下の通りである.
-
"MassDiffusionCoefficients" {{-mc11,-mc12,…},{-mc21,-mc22,…},…} 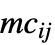 はスカラー,長さ
はスカラー,長さ 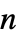 の対角ベクトル,
の対角ベクトル,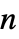 ×
×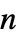 行列のいずれかとして指定できる.
行列のいずれかとして指定できる."MassConservativeConvectionCoefficients" {{-mα11,-mα12,…},{-mα21,-mα22,…},…} 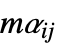 は長さ
は長さ 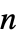 のベクトルである
のベクトルである"MassConvectionCoefficients" {{mβ11,mβ12,…},{mβ21,mβ22,…},…} 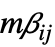 は長さ
は長さ 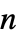 のベクトルである
のベクトルである"MassReactionCoefficients" {{mα11,mα12,…},{mα21,mα22,…},…} 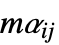 はスカラーである
はスカラーである - "Mass"係数は質量行列
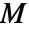 ,"Damping"係数は減衰行列
,"Damping"係数は減衰行列 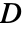 ,残りの係数は剛性行列
,残りの係数は剛性行列 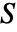 と荷重ベクトル
と荷重ベクトル 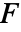 に貢献する.
に貢献する. - NDSolveは,非定常系を簡約し,時間において一階であるようにする.
- 係数は,空間関数,時間関数,パラメータ関数,従属変数関数,従属変数の一次微分の関数のいずれでもよい.
- 変数データ vd と解データ sd は,変数と値の対応するリストである.vd と sd のテンプレートは,NDSolve`VariableDataとNDSolve`SolutionDataを使って生成することができ,成分は,NDSolve`SetSolutionDataComponentを使って設定できる.
- InitializePDECoefficientsは,変数データ vd と解データ sd に従って,係数を確かめ最適化する.
- vd と sd の"Space"成分は,それぞれNumericalRegionオブジェクトとして表された空間変数と空間メッシュに設定されなければならない.
- vd の"DependentVariables"成分は,引数を持たない従属変数名のシンボルのリストでなければならない.
- 時間依存問題については,vd と sd の"Time"成分は,それぞれ時間変数と初期時間に設定されなければならない.
- 非線形問題については,sd の"DependentVariables"成分は,従属変数の初期シード値に設定されなければならない.
- パラメトリック問題については,vd と sd の"Parameters"成分は,それぞれパラメトリック変数と初期パラメトリック値に設定されなければならない.
- InitializePDECoefficientsには以下のオプションがある.
-
"VerificationData" Automatic 偏微分方程式の係数検証データを指定する - InitializePDECoefficientsに与えられるオプションは,"InitializePDECoefficientsOptions"を指定することによってNDSolveに与えることができる. »
- NDSolveおよび関連の関数からオプションを設定することについては,有限要素のためのNDSolveオプションに説明がある.
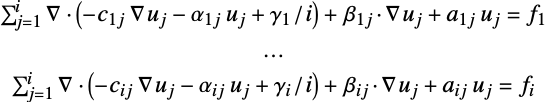
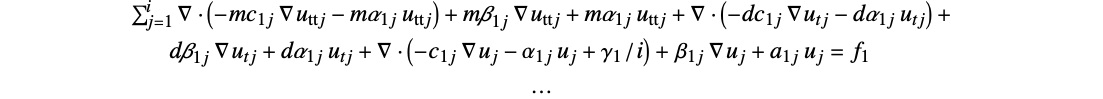
例題
すべて開くすべて閉じる例 (2)
NumericalRegionを設定する:
スコープ (6)
オプション (1)
"VerificationData" (1)
InitializePDECoefficientsに与えられる偏微分方程式の係数は,評価すると数値入力になるように検証される:
検証は,NumericalRegion内に存在する検定座標を求めることによって行われる.しかし,自動的に選ばれた検定座標あるいは検定のElementMarkerが特異点にある場合もある.
検証データから自動的に求められるものを上書きすることは,"VerificationData"オプションを使って行うことができる:
加えて,自動のElementMarkerも変更することができる:
非線形問題では,従属変数と従属変数の微分についての検証データは,それぞれ"DependentVariables"と "DependentVariablesDerivative"を使って変更することができる:
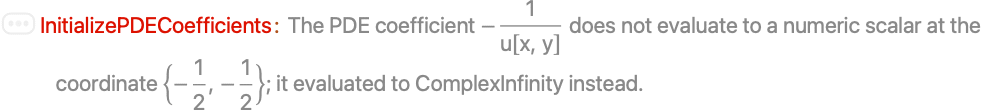
従属変数の微分係数の値をベクトル{1,1}に変更する.ベクトルの成分は,それぞれの空間方向での微分係数の値である.同時にデフォルトの0.1が使われる:
アプリケーション (6)
ラプラス方程式![]() を
を ![]() のときに
のときに ![]() であるディリクレ条件と,
であるディリクレ条件と,![]() のときに
のときに ![]() であるノイマン条件を持つ円板上で指定する:
であるノイマン条件を持つ円板上で指定する:
"LoadCoefficients"係数をNIntegrateで使って,ある領域上で積分する:
NIntegrateを使って結果を確かめる:
"ReactionCoefficients"を![]() とし,例として関数
とし,例として関数 ![]() を評価することができる:
を評価することができる:
"LoadCoefficients"と組み合せた![]() の"ReactionCoefficients"を使って関数をスケールすることができる.例えば,
の"ReactionCoefficients"を使って関数をスケールすることができる.例えば,![]() が領域上で
が領域上で![]() 倍にスケールできる:
倍にスケールできる:
"ReactionCoefficients"を"LoadDerivativeCoefficients"と組み合せて使い,領域上で関数の導関数を補間することができる:
特性と関係 (2)
InitializePDECoefficientsに与えられるオプションは,"InitializePDECoefficientsOptions"を指定することによってNDSolveに与えることができる:
考えられる問題 (1)
通常NDSolveは,係数を評価したときに正しい次元の数量にならない場合に,これを検知して警告を発する:
それぞれの演算子について与えられた係数が適切であるかどうかを確かめるために,この係数は時間の初期点と領域からの座標を使って評価を試行する.係数と使用された値が相殺される場合には,NDSolveは係数が指定されていないのかどうかを検知することができない.その場合NDSolveは,特定の演算子による要素を計算できなかったというメッセージを返す:
上の例では,t=0と x=-π で負荷演算子を評価することによって,負荷演算子が消え,NDSolveは k が指定されていないことを検知することができない:
テキスト
Wolfram Research (2014), InitializePDECoefficients, Wolfram言語関数, https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDECoefficients.html (2024年に更新).
CMS
Wolfram Language. 2014. "InitializePDECoefficients." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDECoefficients.html.
APA
Wolfram Language. (2014). InitializePDECoefficients. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDECoefficients.html