FourierSeries`

NFourierCosCoefficient

gives a numerical approximation to the n coefficient in the Fourier cosine series expansion of expr, where expr is a periodic function of t with period 2π.

Details and Options

To use NFourierCosCoefficient, you first need to load the Fourier Series Package using Needs["FourierSeries`"].
The numerical approximation to the n 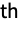coefficient in the Fourier cosine series expansion of expr is by default defined to be 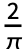NIntegrate[expr Cos[n t],{t,0,π}].
Different choices for the definition of the Fourier cosine series expansion can be specified using the option FourierParameters.
With the setting FourierParameters->{a,b}, expr is assumed to have a period of 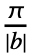, and the n 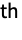coefficient computed by NFourierCosCoefficient is 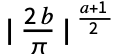NIntegrate[expr Cos[b n t],{t,0,}].
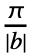The parameter b in the setting FourierParameters->{a,b} must be numeric.
In addition to the option FourierParameters, NFourierCosCoefficient can also accept the options available to NIntegrate. These options are passed directly to NIntegrate.