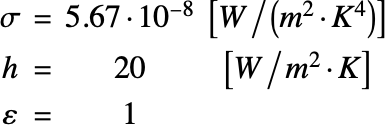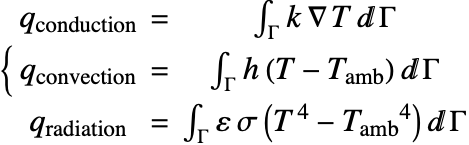Joule Heating of Tungsten Wire
| Introduction | Solve the PDE Model |
| Multiphysics Model | Post-processing and Visualization |
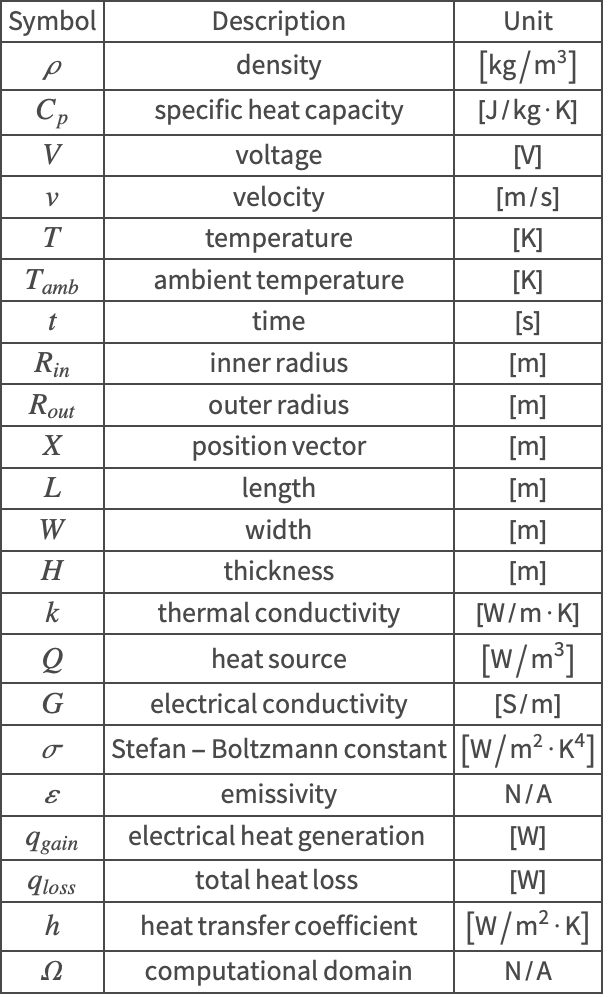
| Domain | Nomenclature |
Introduction
The Joule heating effect (or resistive heating effect) denotes a phenomenon where electric energy is converted into thermal energy as an electric current flows through an object. This effect is commonly found in devices such as electric heaters, incandescent light bulbs and fuses.
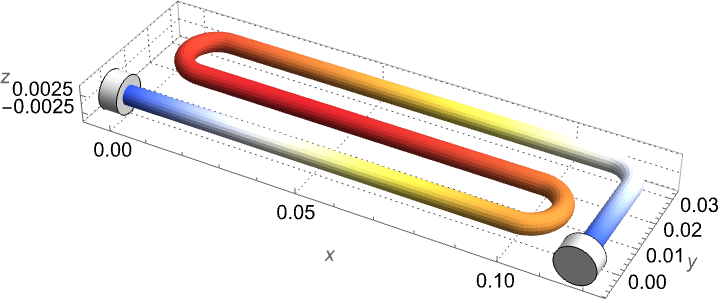
In the following model a voltage of 
is applied to a tungsten wire. Heat is then generated within the wire due to the Joule heating effect. Part of the generated heat dissipates from the side surfaces by both thermal convection and radiation to the surrounding air. The remaining heat propagates towards electrode pads at both ends and leaves the wire by thermal conduction. The electrode pads on both ends act like heat sinks and cool the wire down to the ambient temperature 
.
The electric potential field 
and the total heat generation 
is simulated by an electrostatics model. Based on these result the temperature distribution 
will then be modeled by a heat transfer model. Finally, the amount of heat loss through each surface will calculated and compared.
The symbols and corresponding units used here are summarized in the Nomenclature section.
Please refer to the information provided in "Heat Transfer" for a more general theoretical background for heat transfer analysis.
Multiphysics Model
There are two physical domains involved in this application: the electrostatics model and the heat transfer model. The coupling between two models is one-way only since the temperature field depends on the electric potential but the electric potential field does not depend on the temperature. This type of problem is considered as a sequential multiphysics model, and will be solved in two separate steps.
First the electrostatics model model is built to simulate the potential field 
in the wire. The heat transfer model is then constructed and uses the potential field previously computed to show the Joule heating effect of the wire.
Electrostatics Model
In this model the electric potential field 
is assumed to be independent of the temperature 
. That is, the electrical conductivity 
is kept at a constant value at all time. By Gauss’s law the stationary potential field satisfies Poisson's equation:
Heat Transfer Model
The heat equation (1) is used to solve for the temperature field in a heat transfer model:
For a steady-state heat transfer model the transient term in (2) are set to zero. Since a solid is modeled, the internal velocity 
also vanishes and the heat equation simplifies to:
is the density 
,
is the heat capacity 
,
is the thermal conductivity 
,
is the electrical conductivity 
.
Domain
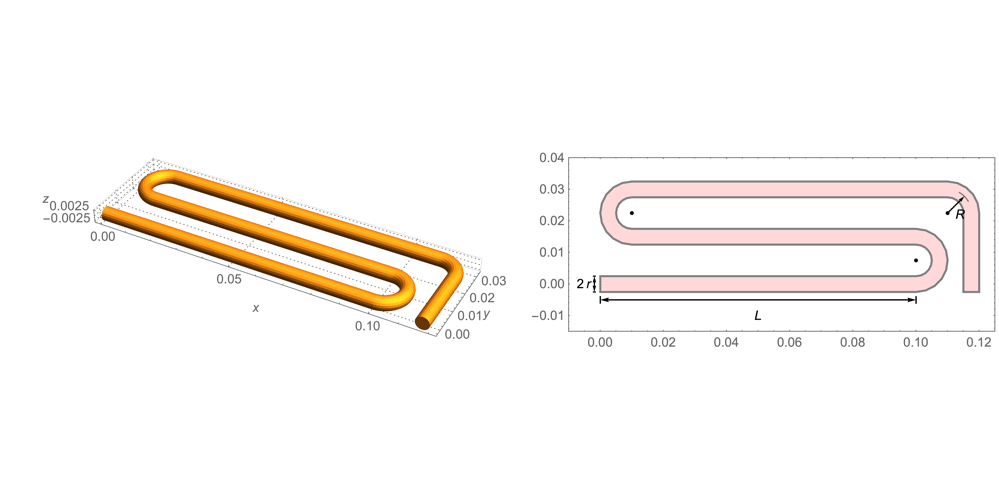
The radius of the tungsten is 
. The simulation domain 
and the geometric shape of the wire are described in the following plot.
Next we construct the 3D domain 
by specifying the path of the tungsten wire.
Now the boundary mesh region and the full element mesh can be generated. In order to get a good result, a finer than the default grid is used for the mesh generation.
In the following sections we will set up the boundary conditions and calculate the heat flux at both ends and the side surfaces. To do so the functions leftEndQ and rightEndQ are defined to determine whether a point 
locates on the corresponding surface.
A tolerance of 
is applied at both ends to account for numerical error in the discretized domain.
Solve the PDE Model
In the following section the electrostatics model will be solved first to simulate the potential field 
of the wire. The heat transfer model is then constructed to show the heating effect of the electric current.
Electrostatics Model
There are two types of the boundary conditions involved in the electrostatics model. At both ends of the wire an electric potential difference 
is applied.
On the remaining boundary a default electrical insulation boundary condition: 
is implicitly used.
Next we visualize the electric potential field 
within the tungsten wire.
Since the electric conductivity 
is homogeneous throughout the wire, the electric potential decreases linearly from left 
to right 
.
With the potential field 
in hand we can calculate the corresponding heat generated by the electric current. The steady-state temperature field 
is then solved for by the heat transfer model in the following section.
Heat Transfer Model
The electrical heat generation is coupled to the stationary heat equation (3) as the source term 
on the right hand side, which is known as the electromagnetic heat source.
Joule's first law (4) states that the heat generated within an object is equivalent to the product of its conductivity 
and the square of the potential gradient.
Before solving the heat transfer PDE model, it is intuitive to inspect the distribution of the electromagnetic heat source 
.
Note that most heat is generated at the inner corners of the wire due to the higher current density in these regions. The total electrical heat generation 
can then be calculated by the volume integration.
The total heat generation is shown to be 
. Next, the heat transfer model is constructed to solve for the steady-state temperature distribution.
There are three types of the boundary conditions involved in the heat transfer model. At both ends of the wire the temperature is fixed at the ambient temperature 
.
On the side surfaces the tungsten wire is losing heat through both thermal convection and radiation. The Stefan-Boltzmann constant 
, the emissivity 
and the heat transfer coefficient 
are given by:
Post-processing and Visualization
To inspect the effect of the Joule heating, we visualize the temperature distribution 
within the tungsten wire.
In the middle portion of the wire the temperature reaches its maximum value at 
. At both ends, however, the temperature is held at the ambient temperature 
.
Next, by computing the boundary integral we can calculate and compare the heat loss on each surface of the wire. As shown in the heat transfer tutorial the heat flux by thermal conduction, convection and radiation are given by
Since the temperature distribution is symmetric along the wire, the amount of the heat conduction should be the same at both ends. Here the difference of 
is the numerical error that can be reduced by using a finer mesh.
The following table summarizes the heat loss through thermal conduction, convection and radiation. It is seen that the tungsten wire loses the majority of the heat it generated through heat conduction at both ends of the wire.
| Power [W] | Ratio [%] | |
| Conduction | 16.28 | 43.8 |
| Convection | 13.24 | 35.7 |
| Radiation | 7.61 | 20.5 |
| Total Heat Loss | 37.13 | 100 |
The total heat loss of the tungsten wire is found as 
. This value can be verified by utilizing the law of energy conservation. That is, in a steady state the total heat loss 
must equal to the internal heat generation 
.
Note that the net heat generation 
matches with the total heat loss 
. A small deviation of 
is a numerical difference introduced by the discrete nature of the finite element mesh used in both cases to compute the heat generation. Using a finer mesh will reduce the numerical error.
