r を m.r にマップするアフィン変換を表すTransformationFunctionを返す.
AffineTransform[{m,v}]
r を m.r+v にマップするアフィン変換を返す.


AffineTransform
r を m.r にマップするアフィン変換を表すTransformationFunctionを返す.
AffineTransform[{m,v}]
r を m.r+v にマップするアフィン変換を返す.
詳細
- AffineTransformはベクトルに適用できるTransformationFunctionを返す.
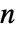 次元の通常のアフィン変換の場合,m は
次元の通常のアフィン変換の場合,m は 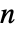 ×
×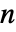 行列である.
行列である.- AffineTransformは,一般に
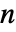 次元の変換で
次元の変換で 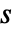 ×
×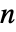 行列をサポートする.
行列をサポートする.
例題
すべて開く すべて閉じるアプリケーション (5)
反復関数系 (3)
画像変換 (2)
関連するガイド
-
▪
- 幾何学変換 ▪
- 計算幾何学 ▪
- 記号的なグラフィックス言語 ▪
- グラフィックスの変形
テキスト
Wolfram Research (2007), AffineTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/AffineTransform.html.
CMS
Wolfram Language. 2007. "AffineTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AffineTransform.html.
APA
Wolfram Language. (2007). AffineTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AffineTransform.html
BibTeX
@misc{reference.wolfram_2025_affinetransform, author="Wolfram Research", title="{AffineTransform}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/AffineTransform.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_affinetransform, organization={Wolfram Research}, title={AffineTransform}, year={2007}, url={https://reference.wolfram.com/language/ref/AffineTransform.html}, note=[Accessed: 07-February-2026]}