gives a TransformationFunction that represents a linear fractional transformation defined by the homogeneous matrix m.
LinearFractionalTransform[{a,b,c,d}]
represents a linear fractional transformation that maps ![]() to
to ![]() .
.


LinearFractionalTransform
gives a TransformationFunction that represents a linear fractional transformation defined by the homogeneous matrix m.
LinearFractionalTransform[{a,b,c,d}]
represents a linear fractional transformation that maps ![]() to
to ![]() .
.
Details
- LinearFractionalTransform gives a TransformationFunction that can be applied to vectors.
- For ordinary linear fractional transforms in n dimensions, m is an
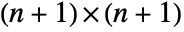 matrix.
matrix. - LinearFractionalTransform in general supports
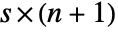 matrices for transformations in
matrices for transformations in 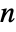 dimensions.
dimensions. - In LinearFractionalTransform[{a,b,c,d}], a is a matrix, b and c are vectors, and d is a scalar.
Examples
open all close allBasic Examples (1)
Scope (3)
If the scalar d is omitted, it is taken to be 1:
A single matrix is taken to be the homogeneous representation of the transform:
Suppose you have a linear fractional transform t:
The inverse is computed by applying InverseFunction:
Related Guides
History
Text
Wolfram Research (2007), LinearFractionalTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/LinearFractionalTransform.html.
CMS
Wolfram Language. 2007. "LinearFractionalTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LinearFractionalTransform.html.
APA
Wolfram Language. (2007). LinearFractionalTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinearFractionalTransform.html
BibTeX
@misc{reference.wolfram_2025_linearfractionaltransform, author="Wolfram Research", title="{LinearFractionalTransform}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/LinearFractionalTransform.html}", note=[Accessed: 16-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_linearfractionaltransform, organization={Wolfram Research}, title={LinearFractionalTransform}, year={2007}, url={https://reference.wolfram.com/language/ref/LinearFractionalTransform.html}, note=[Accessed: 16-January-2026]}