a.b.c or Dot[a,b,c]
gives products of vectors, matrices, and tensors.


Dot 
a.b.c or Dot[a,b,c]
gives products of vectors, matrices, and tensors.
Details

- a.b gives an explicit result when a and b are lists with appropriate dimensions. It contracts the last index in a with the first index in b.
- Various applications of Dot:
-
{a1,a2}.{b1,b2} scalar product of vectors {a1,a2}.{{m11,m12},{m21,m22}}product of a vector and a matrix {{m11,m12},{m21,m22}}.{a1,a2}product of a matrix and a vector {{m11,m12},{m21,m22}}.{{n11,n12},{n21,n22}}product of two matrices - The result of applying Dot to two tensors
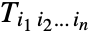 and
and 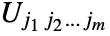 is the tensor
is the tensor 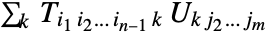 . Applying Dot to a rank
. Applying Dot to a rank 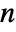 tensor and a rank
tensor and a rank 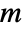 tensor gives a rank
tensor gives a rank 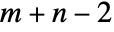 tensor. »
tensor. » - Dot can be used on SparseArray and structured array objects. It will return an object of the same type as the input when possible. »
- Dot is linear in all arguments. » It does not define a complex (Hermitian) inner product on vectors. »
- When its arguments are not lists or sparse arrays, Dot remains unevaluated. It has the attribute Flat.
Examples
open all close allBasic Examples (4)
Scope (28)
Dot Products of Vectors (7)
Scalar product of machine-precision vectors:
Inner product of symbolic vectors:
The dot product of arbitrary-precision vectors:
Dot allows complex inputs, but does not conjugate any of them:
To compute the complex or Hermitian inner product, apply Conjugate to one of the inputs:
Some sources, particularly in the mathematical literature, conjugate the second argument:
Compute the norm of u using the two inner products:
Verify the result using Norm:
Dot product of sparse vectors:
Compute the scalar product of two QuantityArray vectors:
Matrix-Vector Multiplication (5)
Define a rectangular matrix of dimensions ![]() :
:
Define a 2-vector and a 3-vector:
The ![]() matrix can be multiplied by the 2-vector only on the left:
matrix can be multiplied by the 2-vector only on the left:
Multiplying in the opposite order produces an error message due to the incompatible shapes:
Similarly, the ![]() matrix can be multiplied by the 3-vector only on the right:
matrix can be multiplied by the 3-vector only on the right:
Multiply the matrix on both sides at once:
Define a square matrix and a compatible vector:
The products m.v and v.m return different vectors:
The product v.m.v is a scalar:
Define a column and row matrices c and r with the same numerical entries as v:
Products involving m, c and r have the same entries as those involving m and v, but are all matrices:
Moreover, the products must be done in an order that respects the matrices' shapes:
Define a matrix and two vectors:
Since ![]() is a vector,
is a vector, ![]() is an allowed product:
is an allowed product:
Note that it is effectively multiplying ![]() on the left side of the matrix, not the right:
on the left side of the matrix, not the right:
The product of a sparse matrix and sparse vector is a sparse vector:
Format the result as a row matrix:
The product of a sparse matrix and an ordinary vector is a normal vector:
The product of a structured matrix with a vector will retain the structure if possible:
The product of a normal matrix with a structured vector may have the structure of the vector:
Matrix-Matrix Multiplication (11)
Multiply real machine-number matrices:
Visualize the input and output matrices:
Multiply arbitrary-precision matrices:
Since ![]() , these matrices cannot be multiplied in the opposite order:
, these matrices cannot be multiplied in the opposite order:

Product of finite field element matrices:
Product of CenteredInterval matrices:
Find random representatives mrep and nrep of m and n:
Verify that mn contains the product of mrep and nrep:
The product of sparse matrices is another sparse matrix:
The product of structured matrices preserves the structure if possible:
Compare with MatrixPower:
Raise a matrix to the tenth power using Dot in combination with Apply (@@) and ConstantArray:
Higher-Rank Arrays (5)
Dot works for arrays of any rank:
The dimensions of the result are those of the input with the common dimension collapsed:
Any combination is allowed as long as products are done with a common dimension:
Create a rank-three array with three equal dimensions:
Create three vectors of the same dimension:
![]() is the complete contraction
is the complete contraction ![]() that pairs
that pairs ![]() with
with ![]() 's last level and
's last level and ![]() with its first:
with its first:
![]() is the different contraction
is the different contraction ![]() that pairs
that pairs ![]() with
with ![]() 's first level and
's first level and ![]() with its last:
with its last:
Contract both levels of m with the second and third levels of a, respectively:
Dot of two sparse arrays is generally another sparse array:
Dot of a sparse array and an ordinary list may be another sparse array or an ordinary list:
The product of two SymmetrizedArray objects is generally another symmetrized array:
The symmetry of the new array may be much more complicated than the symmetry of either input:
Applications (16)
Projections and Bases (6)
Project the vector ![]() on the line spanned by the vector
on the line spanned by the vector ![]() :
:
Visualize ![]() and its projection onto the line spanned by
and its projection onto the line spanned by ![]() :
:
Project the vector ![]() on the plane spanned by the vectors
on the plane spanned by the vectors ![]() and
and ![]() :
:
First, replace ![]() with a vector in the plane perpendicular to
with a vector in the plane perpendicular to ![]() :
:
The projection in the plane is the sum of the projections onto ![]() and
and ![]() :
:
Find the component perpendicular to the plane:
Confirm the result by projecting ![]() onto the normal to the plane:
onto the normal to the plane:
Visualize the plane, the vector and its parallel and perpendicular components:
Apply the Gram–Schmidt process to construct an orthonormal basis from the following vectors:
The first vector in the orthonormal basis, ![]() , is merely the normalized multiple
, is merely the normalized multiple ![]() :
:
For subsequent vectors, components parallel to earlier basis vectors are subtracted prior to normalization:
Confirm the answers using Orthogonalize:
Verify that the basis is orthonormal:
Find the components of a general vector with respect to this new basis:
Verify the components with respect to the ![]() :
:
Verify that it is a basis by showing that the matrix formed by the vectors has nonzero determinant:
The change of basis matrix is the inverse of the matrix whose columns are the ![]() :
:
A vector whose coordinates are ![]() in the standard bases will have coordinates
in the standard bases will have coordinates ![]() with respect to
with respect to ![]() :
:
Verify that these coordinates give back the vector ![]() :
:
The Frenet–Serret system encodes every space curve's properties in a vector basis and scalar functions. Consider the following curve:
Construct an orthonormal basis from the first three derivatives by subtracting parallel projections:
Ensure that the basis is right-handed:
Compute the curvature, ![]() , and torsion,
, and torsion, ![]() , which quantify how the curve bends:
, which quantify how the curve bends:
Verify the answers using FrenetSerretSystem:
Visualize the curve and the associated moving basis, also called a frame:
Matrices and Linear Operators (6)
A matrix is orthogonal of ![]() . Show that a rotation matrix is orthogonal:
. Show that a rotation matrix is orthogonal:
Confirm using OrthogonalMatrixQ:
A matrix is unitary of ![]() . Show that Pauli matrices are unitary:
. Show that Pauli matrices are unitary:
Confirm with UnitaryMatrixQ:
A matrix is normal if ![]() . Show that the following matrix is normal:
. Show that the following matrix is normal:
Confirm using NormalMatrixQ:
Normal matrices include many other types of matrices as special cases. Unitary matrices are normal:
Hermitian or self-adjoint matrices for which ![]() are also normal, as the matrix
are also normal, as the matrix ![]() shows:
shows:
However, the matrix ![]() is not a named type of normal matrix such as unitary or Hermitian:
is not a named type of normal matrix such as unitary or Hermitian:
In quantum mechanics, systems with finitely many states are represented by unit vectors and physical quantities by matrices that act on them. Consider a spin-1/2 particle such as an electron. It might be in a state such as the following:
The angular momentum in the ![]() direction is given by the following matrix:
direction is given by the following matrix:
The angular momentum of this state is ![]() :
:
The uncertainty in the angular momentum of this state is ![]() :
:
The uncertainty in the ![]() direction is computed analogously:
direction is computed analogously:
The uncertainty principle gives a lower bound on the product of uncertainties, ![]() :
:
Get the matrix representation ![]() for
for ![]() :
:
Create a vector to be acted upon:
Apply the linear mapping to the vector using different methods:
Using ![]() with Dot is the faster method:
with Dot is the faster method:
The application of a single matrix to multiple vectors ![]() can be computed as
can be computed as ![]() :
:
The matrix method is significantly faster than repeated application:
Matrices and Arrays with Symmetry (4)
A real symmetric matrix ![]() gives a quadratic form
gives a quadratic form ![]() by the formula
by the formula ![]() :
:
Quadratic forms have the property that ![]() :
:
Equivalently, they define a homogeneous quadratic polynomial in the variables of ![]() :
:
The range of the polynomial can be ![]() ,
, ![]() ,
, ![]() or
or ![]() . In this case it is
. In this case it is ![]() :
:
A positive-definite, real symmetric matrix or metric ![]() defines an inner product by
defines an inner product by ![]() :
:
Being positive-definite means that the associated quadratic form ![]() is positive for
is positive for ![]() :
:
Note that Dot itself is the inner product associated with the identity matrix:
Apply the Gram–Schmidt process to the standard basis to obtain an orthonormal basis:
Confirm that this basis is orthonormal with respect to the inner product ![]() :
:
An antisymmetric matrix ![]() for which
for which ![]() defines a Hamiltonian 2-form
defines a Hamiltonian 2-form ![]() :
:
However, the form is nondegenerate, meaning ![]() implies
implies ![]() :
:
Construct six vectors in dimension six:
Construct the totally antisymmetric array in dimension six using LeviCivitaTensor:
Compute the complete contraction ![]() :
:
This is equal to the determinant of the matrix formed by the vectors:
By the antisymmetry of ![]() , the reversed contraction differs by
, the reversed contraction differs by ![]() in dimension
in dimension ![]() :
:
Properties & Relations (16)
Dot is linear in each argument:
For a vector ![]() with real entries, Norm[v] equals
with real entries, Norm[v] equals ![]() :
:
For a vector with complex values, the norm is given by ![]() :
:
For two vectors with real entries, ![]() , with
, with ![]() the angle between
the angle between ![]() and
and ![]() :
:
The scalar product of vectors is invariant under rotations:
For two matrices, the ![]() ,
, ![]()
![]() entry of
entry of ![]() is the dot product of the
is the dot product of the ![]()
![]() row of
row of ![]() with the
with the ![]()
![]() column of
column of ![]() :
:
Matrix multiplication is non-commutative, ![]() :
:
Use MatrixPower to compute repeated matrix products:
Compare with a direct computation:
The action of b on a vector is the same as acting four times with a on that vector:
For two tensors ![]() and
and ![]() ,
, ![]() is the tensor
is the tensor ![]() :
:
Applying Dot to a rank-![]() tensor and a rank-
tensor and a rank-![]() tensor gives a rank-
tensor gives a rank-![]() tensor:
tensor:
Dot with two arrays is a special case of Inner:
Dot implements the standard inner product of arrays:
Use Times to do elementwise multiplication:
Dot can be implemented as a combination of TensorProduct and TensorContract:
Use Dot in combination with Flatten to contract multiple levels of one array with those of another:
TensorReduce can simplify expressions involving Dot:
Outer of two vectors can be computed with Dot:
Construct the column and row matrices corresponding to u and v:
Dot of a row and column matrix equals the KroneckerProduct of the corresponding vectors:
Possible Issues (2)
Dot effectively treats vectors multiplied from the right as column vectors:
Dot effectively treats vectors multiplied from the left as row vectors:
Dot does not give the standard inner product on ![]() :
:
Use Conjugate in one argument to get the Hermitian inner product:
Check that the result coincides with the square of the norm of a:
See Also
MatrixPower Cross Norm KroneckerProduct Inner Outer Times Div TensorContract TensorProduct AffineTransform NonCommutativeMultiply VectorAngle Covariance LinearLayer DotLayer
Function Repository: FromTensor
Tech Notes
Related Links
History
Introduced in 1988 (1.0) | Updated in 2003 (5.0) ▪ 2012 (9.0) ▪ 2024 (14.0)
Text
Wolfram Research (1988), Dot, Wolfram Language function, https://reference.wolfram.com/language/ref/Dot.html (updated 2024).
CMS
Wolfram Language. 1988. "Dot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Dot.html.
APA
Wolfram Language. (1988). Dot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Dot.html
BibTeX
@misc{reference.wolfram_2025_dot, author="Wolfram Research", title="{Dot}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Dot.html}", note=[Accessed: 07-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_dot, organization={Wolfram Research}, title={Dot}, year={2024}, url={https://reference.wolfram.com/language/ref/Dot.html}, note=[Accessed: 07-January-2026]}