ArrayDot

ArrayDot[a,b,k]

a の最後の k 次元と b の最初の k 次元の項の積を合計することで得られた配列 a と配列 b の積を計算する．

ArrayDot[a,b,{{s1,t1},{s2,t2},…}]

次元のペア{si,ti}の項の積を合計することで得られた配列 a と配列 b の積を計算する．

詳細

  • ArrayDot[a,b,k]の引数 a と b は，それぞれ次元が{m1,…,mp,d1,…,dk}と{d1,…,dk,n1,…,nq}の配列でなければならない．結果は次元が{m1,…,mp,n1,…,nq}の配列 c で， ci1,…,ip,j1,…,jq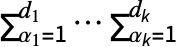sum_(alpha_(1)=1)^(d_(1))...sum_(alpha_k=1)^(d_k)ai1,…,ip,α1,…,αkbα1,…,αk,j1,…,jqである．
  • ArrayDot[a,b,{{s1,t1},…,{sk,tk}}]の引数 a と b は次元がそれぞれ{m1,…,mp}と{n1,…,nq}の配列でなければならない．ここで，すべての siと tiは他と異なり，すべての i について1≤si≤p，1≤ti≤q，msintiである．結果はTensorContract[ab,{{s1,p+t1},…,{sk,p+tk}}]に等しい．
  • ArrayDotは，SparseArrayオブジェクトおよび構造化配列オブジェクトに使うことができる．
  • ArrayDotは，配列微分連鎖法則に使用される．

例題

すべて開くすべて閉じる

例  (3)

2つの次元でArrayDotを計算する：

指定された次元のペアでArrayDotを計算する：

ArrayDotは配列微分連鎖法則に使用される：

スコープ  (9)

数の配列を抽出する：

機械精度の実数配列：

複素数配列：

記号配列：

有限体要素の配列：

CenteredInterval配列：

a と b のランダムな代表 arep と brep：

ArrayDot[a,b,3]がArrayDot[arep,brep,3]を含んでいることを確認する：

疎な配列のArrayDotは，疎な配列である：

結果をフォーマットする：

構造化配列：

大きい配列の乗算を効率的に行う：

アプリケーション  (1)

摂動行列の行列式を近似する：

次数0の近似：

厳密値と比較する：

次数1の近似：

厳密値と比較する：

次数2の近似：

厳密値と比較する：

特性と関係  (9)

ArrayDotは，各引数において線形である：

Dot[a,b]はArrayDot[a,b,1]に等しい：

SymbolicIdentityArrayはArrayDotの単位元である：

厳密行列 a について，Norm[a,"Frobenius"]はArrayDot[a,a,2]の平方根に等しい：

c=ArrayDot[a,b, k]なら ci1,…,ip,j1,…,jqsum_(alpha_(1)=1)^(d_(1))...sum_(alpha_k=1)^(d_k)ai1,…,ip,α1,…,αkbα1,…,αk,j1,…,jqである：

ArrayDepth[ArrayDot[a,b,k]]はArrayDepth[a]+ArrayDepth[b]-2kに等しい：

ArrayDotはTensorProductとTensorContractの組合せとして実装できる：

ArrayDotはFlattenとDotの組合せとして実装できる：

ArrayDotは，配列の微分連鎖律で使われる：

Wolfram Research (2024), ArrayDot, Wolfram言語関数， https://reference.wolfram.com/language/ref/ArrayDot.html.

テキスト

Wolfram Research (2024), ArrayDot, Wolfram言語関数， https://reference.wolfram.com/language/ref/ArrayDot.html.

CMS

Wolfram Language. 2024. "ArrayDot." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArrayDot.html.

APA

Wolfram Language. (2024). ArrayDot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArrayDot.html

BibTeX

@misc{reference.wolfram_2024_arraydot, author="Wolfram Research", title="{ArrayDot}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ArrayDot.html}", note=[Accessed: 04-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_arraydot, organization={Wolfram Research}, title={ArrayDot}, year={2024}, url={https://reference.wolfram.com/language/ref/ArrayDot.html}, note=[Accessed: 04-November-2024 ]}