ArrayDot

ArrayDot[a,b,k]

计算数组 a 和 b 的乘积，该乘积是通过对 a 的后 k 维和 b 的前 k 维的项的乘积求和而获得.

ArrayDot[a,b,{{s1,t1},{s2,t2},…}]

计算数组 a 和 b 的乘积，该乘积是通过通过对维度对 {si,ti} 上各项的乘积求和获得.

更多信息

  • ArrayDot[a,b,k] 中的参数 a 和 b 应分别为具有维度 {m1,…,mp,d1,…,dk} 和 {d1,…,dk,n1,…,nq} 的数组. 结果是一个数组 c，维度为 {m1,…,mp,n1,…,nq} 和ci1,…,ip,j1,…,jq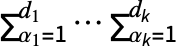sum_(alpha_(1)=1)^(d_(1))...sum_(alpha_k=1)^(d_k)ai1,…,ip,α1,…,αkbα1,…,αk,j1,…,jq.
  • 在 ArrayDot[a,b,{{s1,t1},…,{sk,tk}}] 中，参数 a 和 b 应分别为具有维度 {m1,…,mp} 和 {n1,…,nq} 的数组，其中所有 si 是不同的，所有 ti 是不同的，并且对于所有 i，1≤si≤p，1≤ti≤q 且 msinti. 该结果等于 TensorContract[ab,{{s1,p+t1},…,{sk,p+tk}}].
  • ArrayDot 可以用于 SparseArray 和结构化数组对象.
  • ArrayDot 用于数组微分链式法则.

范例

打开所有单元关闭所有单元

基本范例  (3)

在两个维度上计算 ArrayDot：

在指定的维度对上计算 ArrayDot：

ArrayDot 用于数组微分链式法则：

范围  (9)

精确数值数组：

实机器数数组：

复数数组：

符号数组：

有限域元素数组：

CenteredInterval 数组：

求 a 和 b 的随机表示 arep 和 brep：

验证 ArrayDot[a,b,3] 包含 ArrayDot[arep,brep,3]：

稀疏数组的 ArrayDot 是也是稀疏数组：

格式化结果：

结构化数组：

有效地乘以大型数组：

应用  (1)

近似扰动矩阵的行列式：

零阶近似：

与精确值进行比较：

一阶近似：

与精确值进行比较：

二阶近似：

与精确值进行比较：

属性和关系  (9)

ArrayDot 对于每个参数都是线性的：

Dot[a,b] 等于 ArrayDot[a,b,1]：

SymbolicIdentityArray 对象是 ArrayDot 的恒等元素：

对于实数矩阵 a，Norm[a,"Frobenius"] 等于 ArrayDot[a,a,2] 的平方根：

如果 c=ArrayDot[a,b, k]，则 ci1,…,ip,j1,…,jqsum_(alpha_(1)=1)^(d_(1))...sum_(alpha_k=1)^(d_k)ai1,…,ip,α1,…,αkbα1,…,αk,j1,…,jq：

ArrayDepth[ArrayDot[a,b,k]] 等于 ArrayDepth[a]+ArrayDepth[b]-2k：

ArrayDot 可以作为 TensorProduct 和 TensorContract 的组合来实现：

ArrayDot 可以作为 Flatten 和 Dot 的组合来实现：

ArrayDot 用于数组微分链式法则：

Wolfram Research (2024)，ArrayDot，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ArrayDot.html.

文本

Wolfram Research (2024)，ArrayDot，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ArrayDot.html.

CMS

Wolfram 语言. 2024. "ArrayDot." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ArrayDot.html.

APA

Wolfram 语言. (2024). ArrayDot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ArrayDot.html 年

BibTeX

@misc{reference.wolfram_2024_arraydot, author="Wolfram Research", title="{ArrayDot}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ArrayDot.html}", note=[Accessed: 04-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_arraydot, organization={Wolfram Research}, title={ArrayDot}, year={2024}, url={https://reference.wolfram.com/language/ref/ArrayDot.html}, note=[Accessed: 04-November-2024 ]}