AsymptoticEqual[f,g,xx*]
gives conditions for ![]() or
or ![]() as xx*.
as xx*.
AsymptoticEqual[f,g,{x1,…,xn}{![]() ,…,
,…,![]() }]
}]
gives conditions for ![]() or
or ![]() as {x1,…,xn}{
as {x1,…,xn}{![]() ,…,
,…,![]() }.
}.


AsymptoticEqual
AsymptoticEqual[f,g,xx*]
gives conditions for ![]() or
or ![]() as xx*.
as xx*.
AsymptoticEqual[f,g,{x1,…,xn}{![]() ,…,
,…,![]() }]
}]
gives conditions for ![]() or
or ![]() as {x1,…,xn}{
as {x1,…,xn}{![]() ,…,
,…,![]() }.
}.
Details and Options




- Asymptotic equal is also expressed as f is big-theta of g, f is bounded by g, f is of order g, and f grows as g. The point x* is often assumed from context.
- Asymptotic equal is an equivalence relation and means
![c_1 TemplateBox[{{g, (, x, )}}, Abs]<=TemplateBox[{{f, (, x, )}}, Abs]<=c_2 TemplateBox[{{g, (, x, )}}, Abs] c_1 TemplateBox[{{g, (, x, )}}, Abs]<=TemplateBox[{{f, (, x, )}}, Abs]<=c_2 TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticEqual.en/9.png) when x is near x* for some constants
when x is near x* for some constants 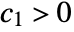 and
and 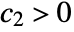 . It is a coarser asymptotic equivalence relation than AsymptoticEquivalent.
. It is a coarser asymptotic equivalence relation than AsymptoticEquivalent. - Typical uses include expressing simple bounds for functions and sequences near some point. It is frequently used for asymptotic solutions to equations and to give simple lower bounds for computational complexity.
- For a finite limit point x* and {
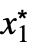 ,…,
,…,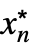 }, the result is:
}, the result is: -
AsymptoticEqual[f[x],g[x],xx*] there exist 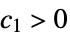 ,
, 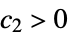 and
and 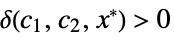 such that
such that ![0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<delta(c_1,c_2,x^*) 0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<delta(c_1,c_2,x^*)](Files/AsymptoticEqual.en/17.png) implies
implies ![c_1 TemplateBox[{{g, (, x, )}}, Abs]<=TemplateBox[{{f, (, x, )}}, Abs]<=c_2 TemplateBox[{{g, (, x, )}}, Abs] c_1 TemplateBox[{{g, (, x, )}}, Abs]<=TemplateBox[{{f, (, x, )}}, Abs]<=c_2 TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticEqual.en/18.png)
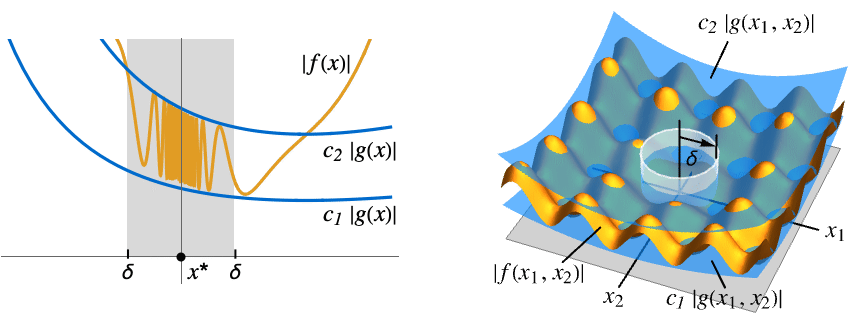
AsymptoticEqual[f[x1,…,xn],g[x1,…,xn],{x1,…,xn}{ 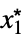 ,…,
,…,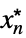 }]
}]there exist 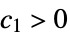 ,
, 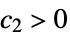 and
and 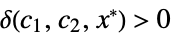 such that
such that ![0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<delta(epsilon,x^*) 0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<delta(epsilon,x^*)](Files/AsymptoticEqual.en/24.png) implies
implies ![c_1 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=c_2 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs] c_1 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=c_2 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]](Files/AsymptoticEqual.en/25.png)
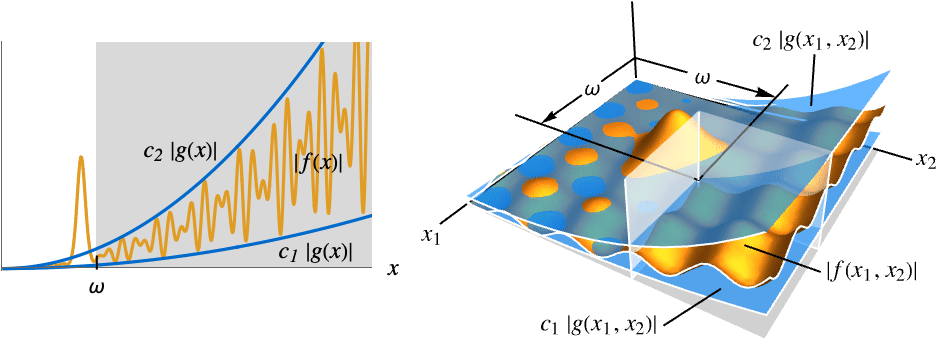
- For an infinite limit point, the result is:
-
AsymptoticEqual[f[x],g[x],x∞] there exist 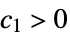 ,
, 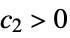 and
and 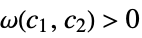 such that
such that 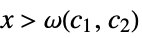 implies
implies ![c_1 TemplateBox[{{g, (, x, )}}, Abs]<=TemplateBox[{{f, (, x, )}}, Abs]<=c_2 TemplateBox[{{g, (, x, )}}, Abs] c_1 TemplateBox[{{g, (, x, )}}, Abs]<=TemplateBox[{{f, (, x, )}}, Abs]<=c_2 TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticEqual.en/31.png)
AsymptoticEqual[f[x1,…,xn],g[x1,…,xn],{x1,…,xn}{∞,…,∞}] there exist 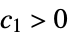 ,
, 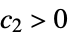 and
and 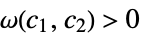 such that
such that 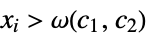 implies
implies ![c_1 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=c_2 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs] c_1 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=c_2 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]](Files/AsymptoticEqual.en/36.png)
- AsymptoticEqual[f[x],g[x],xx*] exists if and only if MinLimit[Abs[f[x]/g[x]],xx*]>0 and MaxLimit[Abs[f[x]/g[x]],xx*]<∞ when g[x] does not have an infinite set of zeros near x*.
- The following options can be given:
-
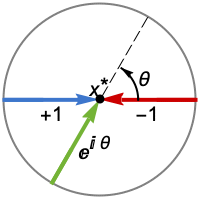
Assumptions $Assumptions assumptions on parameters Direction Reals direction to approach the limit point GenerateConditions Automatic generate conditions for parameters Method Automatic method to use PerformanceGoal "Quality" what to optimize - Possible settings for Direction include:
-
Reals or "TwoSided" from both real directions "FromAbove" or -1 from above or larger values "FromBelow" or +1 from below or smaller values Complexes from all complex directions Exp[ θ] in the direction 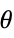
{dir1,…,dirn} use direction diri for variable xi independently - DirectionExp[ θ] at x* indicates the direction tangent of a curve approaching the limit point x*.
- Possible settings for GenerateConditions include:
-
Automatic non-generic conditions only True all conditions False no conditions None return unevaluated if conditions are needed - Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, Limit typically solves more problems or produces simpler results, but it potentially uses more time and memory.
Examples
open all close allBasic Examples (2)
Scope (9)
Compare functions that are not strictly positive:
Show that ![]() diverges at the same rate as
diverges at the same rate as ![]() at the origin:
at the origin:
Answers may be Boolean expressions rather than explicit True or False:
When comparing functions with parameters, conditions for the result may be generated:
By default, a two-sided comparison of the functions is made:
When comparing larger values of ![]() ,
, ![]() vanishes at the same rate as
vanishes at the same rate as ![]() :
:
The relationship fails for smaller values of ![]() :
:
Visualize the ratio of the two functions, showing it approaches a nonzero limit from above:
Functions like Sqrt may have the same relationship in both real directions along the negative reals:
If approached from above in the complex plane, the same relationship is observed:
However, approaching from below in the complex plane produces a different result:
This is due to a branch cut where the imaginary part of Sqrt reverses sign as the axis is crossed:
Hence, the relationship does not hold in the complex plane in general:
Visualize the relative sizes of the functions when approached from the four real and imaginary directions:
Compare multivariate functions:
Visualize the norms of the two functions:
Options (9)
Assumptions (1)
Specify conditions on parameters using Assumptions:
Direction (5)
Equality at piecewise discontinuities:
Since it fails in one direction, the two-sided result is false as well:
Visualize the two functions and their ratio:
Equality at a pole is independent of the direction of approach:
Compute equality, approaching from different quadrants:
Approaching the origin from the third quadrant:
Approaching the origin from the second quadrant:
Approaching the origin from the right half-plane:
GenerateConditions (3)
Return a result without stating conditions:
This result is only valid if n>0:
Return unevaluated if the results depend on the value of parameters:
By default, conditions are not generated if only special values invalidate the result:
With GenerateConditions->True, even these non-generic conditions are reported:
Applications (10)
Basic Applications (5)
Show that two monomials equivalent at infinity have the same power:
Use this to show that two polynomials that are equivalent are of the same order:
Visualize the ratios of three pairs of asymptotically equivalent polynomials:
Show that two monomials in ![]() equivalent at
equivalent at ![]() have the same power:
have the same power:
Use this to show that two polynomials in ![]() that are equivalent have the same leading monomial:
that are equivalent have the same leading monomial:
Visualize the ratios of three pairs of asymptotically equivalent polynomials in ![]() :
:
Even though the absolute value of their ratio wiggles incessantly as ![]() , it is bounded away from
, it is bounded away from ![]() :
:
Even though the absolute value of their ratio wiggles incessantly as ![]() , it is bounded away from
, it is bounded away from ![]() :
:
Computational Complexity (3)
In a bubble sort, adjoining neighbors are compared and swapped if they are out of order. After one pass of n-1 comparisons, the largest element is at the end. The process is then repeated on remaining n-1 elements, and so forth, until only two elements at the very beginning remain. If comparison and swap takes c steps, the total number of steps for the sort is as follows:
Show that ![]() , and thus the algorithm has quadratic run time:
, and thus the algorithm has quadratic run time:
Visualize the ratios for the two functions for different values of c:
In a merge sort, the list of elements is split in two, each half is sorted, and then the two halves are combined. Thus, the time T[n] to do the sort will be the sum of some constant time b to compute the middle, 2T[n/2] to sort each half, and some multiple a n of the number of elements to combine the two halves:
Solve the recurrence equation to find the time t to sort n elements:
Show that ![]() , and thus the algorithm has
, and thus the algorithm has ![]() run time:
run time:
Strassen's algorithm was the first subcubic matrix multiplication algorithm found. It consists of four steps: splitting each of the two ![]() matrices into 4 equal-sized submatrices, forming 14 particular linear combinations out of the 8 submatrices, multiplying 7 pairs of these and forming linear combinations of the 7 results. The time
matrices into 4 equal-sized submatrices, forming 14 particular linear combinations out of the 8 submatrices, multiplying 7 pairs of these and forming linear combinations of the 7 results. The time ![]() to do the multiplication will therefore be a constant time
to do the multiplication will therefore be a constant time ![]() to split the matrix,
to split the matrix, ![]() for forming linear combinations in the second and fourth steps and
for forming linear combinations in the second and fourth steps and ![]() for the third step:
for the third step:
Solve the recurrence relation:
Though the result is complicated, it is asymptotically equal to ![]() :
:
Compare the rate of growth of the naive cubic algorithm and Strassen's algorithm:
Convergence Testing (2)
A sequence ![]() is said to be absolutely summable if
is said to be absolutely summable if ![]() . If a second sequence
. If a second sequence ![]() , the comparison test states that
, the comparison test states that ![]() is absolutely summable if and only if
is absolutely summable if and only if ![]() is. Use the test to show that
is. Use the test to show that ![]() converges by comparing with the sum of
converges by comparing with the sum of ![]() :
:
Compare with the answer given by SumConvergence:
Show that ![]() convergence by comparing with the sum of
convergence by comparing with the sum of ![]() :
:
Show that ![]() divergence by comparing with the sum of
divergence by comparing with the sum of ![]() :
:
Compare with the answer given by SumConvergence:
The sequence ![]() , and thus is not absolutely summable:
, and thus is not absolutely summable:
A function ![]() is said to be absolutely integrable on
is said to be absolutely integrable on ![]() if
if ![]() . If
. If ![]() and
and ![]() are continuous on the open interval
are continuous on the open interval ![]() and
and ![]() at both
at both ![]() and
and ![]() , the comparison test states that
, the comparison test states that ![]() is absolutely integrable if and only if
is absolutely integrable if and only if ![]() is. Use the test to show that
is. Use the test to show that ![]() is absolutely integrable on
is absolutely integrable on ![]() :
:
Since ![]() is integrable on
is integrable on ![]() , so is
, so is ![]() :
:
That ![]() is not integrable over
is not integrable over ![]() can be shown by comparing it with
can be shown by comparing it with ![]() :
:
The result follows from the nonintegrability of ![]() on the unit interval:
on the unit interval:
The function ![]() is not absolutely integrable on
is not absolutely integrable on ![]() :
:
Show that ![]() is not absolutely integrable either, by comparing it to
is not absolutely integrable either, by comparing it to ![]() :
:
Properties & Relations (6)
AsymptoticEqual is an equivalence relation, meaning it is reflexive (![]() ):
):
It is transitive (![]() and
and ![]() implies
implies ![]() ):
):
And it is symmetric (![]() implies
implies ![]() ):
):
AsymptoticEqual[f[x],g[x],xx0] iff MaxLimit[Abs[f[x]/g[x]],xx0]<∞ and MinLimit[Abs[f[x]/g[x]],xx0]>0:
AsymptoticEqual[f[x],g[x],xx0] if 0<Limit[Abs[f[x]/g[x]],xx0]<∞:
However, the limit need not exist:
The converse, however, is false:
The converse is false, so AsymptoticEqual is coarser than AsymptoticEquivalent:
Related Guides
History
Text
Wolfram Research (2018), AsymptoticEqual, Wolfram Language function, https://reference.wolfram.com/language/ref/AsymptoticEqual.html.
CMS
Wolfram Language. 2018. "AsymptoticEqual." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AsymptoticEqual.html.
APA
Wolfram Language. (2018). AsymptoticEqual. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AsymptoticEqual.html
BibTeX
@misc{reference.wolfram_2025_asymptoticequal, author="Wolfram Research", title="{AsymptoticEqual}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/AsymptoticEqual.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_asymptoticequal, organization={Wolfram Research}, title={AsymptoticEqual}, year={2018}, url={https://reference.wolfram.com/language/ref/AsymptoticEqual.html}, note=[Accessed: 06-March-2026]}