AsymptoticEqual

AsymptoticEqual[f,g,xx^*]

xx^*のときのまたはの条件を与える．

AsymptoticEqual[f,g,{x₁,…,x_n}{,…,}]

{x₁,…,x_n}{,…,}のときのまたはの条件を与える．

詳細とオプション

「漸近的に等しい」は，f は g の「big-theta」である，f g によって有界である，f は g 程度である，f は g と同じように成長する，等とも表現される．点 x^*はコンテキストから推測されることが多い．
「漸近的に等しい」は同値関係で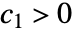，かつ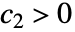である定数について，x が x^*の近くにあるときに $c_1 TemplateBox[{{g, (, x, )}}, Abs]<=TemplateBox[{{f, (, x, )}}, Abs]<=c_2 TemplateBox[{{g, (, x, )}}, Abs]$ であることを意味する．これは，AsymptoticEquivalentよりもきめが粗い漸近的同値関係である．
点の近くの関数や級数の単純な表現のため，方程式の漸近解のため，複雑な計算で単純に下限を表すためにしばしば用いられる．
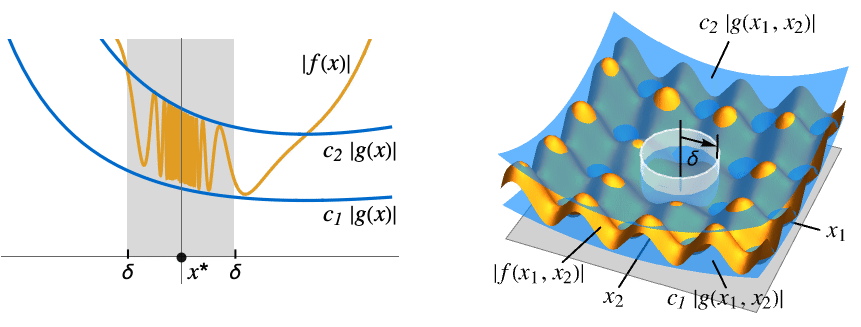
有限極限点の x^*および{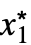,…,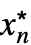}については以下のようになる．

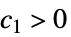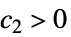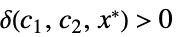	AsymptoticEqual[f[x],g[x],xx^*]	$0<TemplateBox[{{x, -, {x, ^, }}}, Abs]<delta(c_1,c_2,x^)$ が $c_1 TemplateBox[{{g, (, x, )}}, Abs]<=TemplateBox[{{f, (, x, )}}, Abs]<=c_2 TemplateBox[{{g, (, x, )}}, Abs]$ を意味する，，が存在する
	AsymptoticEqual[f[x₁,…,x_n],g[x₁,…,x_n],{x₁,…,x_n}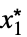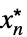{,…,}]	$0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, }}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, }}}, }}}, Norm]<delta(epsilon,x^*)$ が $c_1 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=c_2 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]$ を意味する，，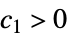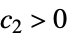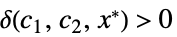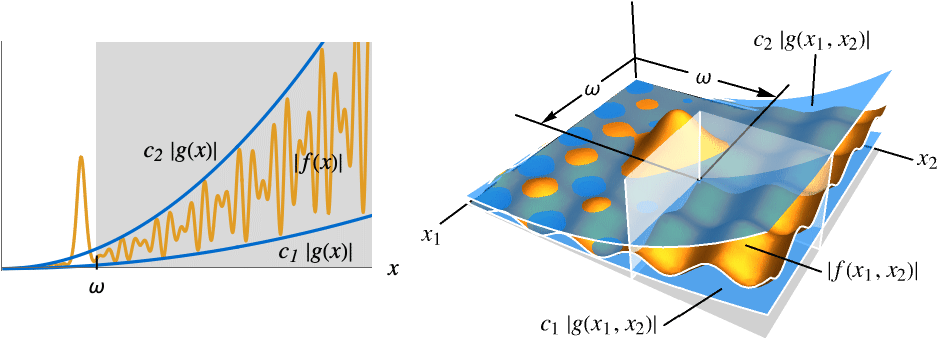が存在する

無限極限点については以下のようになる．

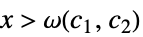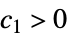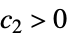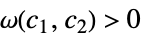	AsymptoticEqual[f[x],g[x],x∞]	が $c_1 TemplateBox[{{g, (, x, )}}, Abs]<=TemplateBox[{{f, (, x, )}}, Abs]<=c_2 TemplateBox[{{g, (, x, )}}, Abs]$ を意味する，，が存在する
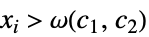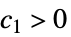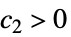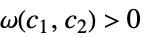	AsymptoticEqual[f[x₁,…,x_n],g[x₁,…,x_n],{x₁,…,x_n}{∞,…,∞}]	が $c_1 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]<=c_2 TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]$ を意味する，，が存在する

g[x]が x^*付近に0の無限集合を持たない場合，AsymptoticEqual[f[x],g[x],xx^*]は，MinLimit[Abs[f[x]/g[x]],xx^*]>0かつMaxLimit[Abs[f[x]/g[x]],xx^*]<∞のときかつそのときに限り存在する．
次は，使用可能なオプションである．

Assumptions	$Assumptions	パラメータについての仮定
Direction	Reals	極限点に近付く方向
GenerateConditions	Automatic	パラメータについての条件を生成する
Method	Automatic	使用するメソッド
PerformanceGoal	"Quality"	何を最適化するか

次は，Directionの可能な設定である．

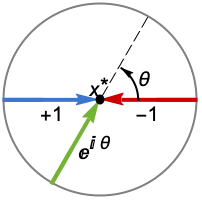
	Reals または "TwoSided"	両実数方向から
	"FromAbove" または -1	上，つまり大きい値から
	"FromBelow" または +1	下，つまり小さい値から
	Complexes	すべての複素方向から
	Exp[ θ]	の方向
	{dir₁,…,dir_n}	変数 x_iに方向 dir_iを使う

x^*におけるDirectionExp[ θ]は，曲線の接線が極限点 x^*に近付く方向を示す．

次は，GenerateConditionsの可能な設定である．
Automatic 一般的ではない条件のみ

True すべての条件

False 条件なし

None 条件が必要な場合には未評価で返す
PerformanceGoalの可能な設定には，$PerformanceGoal，"Quality"，"Speed"がある．"Quality"設定のとき，Limitはより多くの問題を解いたり，より簡単な結果を与えたりすることが多いが，より多くの時間とメモリが必要になる可能性がある．

例題

すべて開くすべて閉じる

例 (2)

のときに，であることを検証する：

前者は後者の2つの定倍数に挟まれるかもしれない：

のときに，であることを検証する：

前者は後者の2つの定倍数に挟まれるかもしれない：

スコープ (9)

厳密には正ではない関数を比較する：

がと同じ割合で原点付近で発散することを示す：

答は明示的なTrueまたはFalseではなく，ブール式かもしれない：

パラメータを含む関数を比較する場合は，結果についての条件が生成されることがある：

デフォルトで，関数の両側比較が行われる：

のより大きい値を比較する場合は，は $x^2(1-cos(x)) TemplateBox[{{x}}, UnitStepSeq]$ と同じ割合で消失する：

この関係は，のより小さい値については成り立たない：

上から非零の極限に近付くときの2つの関数の割合を可視化する：

Sqrtのような関数は，負の実数に沿って両方の実数方向で同じ関係を持つかもしれない：

複素平面で上から近付く場合には，同じ関係が見られる：

しかし，複素平面で下から近付く場合は異なる結果になる：

これは，軸が交差するときにSqrtの虚部の符号が逆になるところで分枝切断されているためである：

したがって，この関係は，一般に，複素平面では成り立たない：

4つの実数方向および複素数方向から近付く場合の関数の相対サイズを可視化する：

多変量関数を比較する：

2つの関数のノルムを可視化する：

多変量関数を無限大で比較する：

多変量関数を比較する際にパラメータを使用する：

オプション (9)

Assumptions (1)

Assumptionsを使ってパラメータについての条件を指定する：

異なる仮定に対しては，異なる結果が生成されるかもしれない：

Direction (5)

下からの等価性：

同様に：

上からの等価性：

同様に：

区分的不連続点における等価性：

片方の方向でうまくいかないので，両方からもうまくいかない：

2関数とその割合を可視化する：

極における等価性は近付く方向とは無関係である：

分枝切断線における等価性：

異なる象限から近付く際の等価性を計算する：

第3象限から原点に近付く：

同様に：

第2象限から原点に近付く：

右半平面から原点に近付く：

下半平面から原点に近付く：

この関数の割合を可視化する：

GenerateConditions (3)

条件を述べずに結果を返す：

この結果は n>0のときしか有効ではない：

結果がパラメータの値に依存する場合は未評価で返される：

デフォルトで，特殊な値でしか結果が無効にならないときは，条件は生成されない：

GenerateConditions->Trueのときは，それら一般的ではない条件さえもがレポートされる：

アプリケーション (10)

基本的なアプリケーション (5)

無限大において等しい2つの単項式のベキが等しいことを示す：

これを使って，等価である2つの多項式の次数が等しいことを示す：

漸近的に等しい3対の多項式の割合を可視化する：

中のにおいて等しい2つの単項式のベキが等しいことを示す：

これを使って，中の等価である2つの多項式の先頭単項式が等しいことを示す：

中の漸近的に等しい3対の多項式の割合を可視化する：

においてであることを示す：

関数を可視化する：

のとき，両者の割合の絶対値は絶え間無く変動するが，で有界である：

であることを示す：

のとき，これらの割合の絶対値は絶え間無く変動するが，で有界である：

においてであることを示す：

計算の複雑性 (3)

バブルソートでは，隣接近傍が比較され，順序が狂っている場合には入れ替えられる．1回のパス（n-1 回の比較）の後で最大要素が末尾になる．このプロセスが残りの n-1個の要素に対して行われ，先頭の2つの要素が残るまでこれが繰り返される．比較と入替えが c ステップだとすると，ソートのステップ総数は次のようになる：

であり，したがってこのアルゴリズムのランタイムが2次であることを示す：

c の異なる値についての2つの関数の割合を可視化する：

マージソートでは，要素のリストが2つに分割され，半分ずつソートされ，最後に2つの部分が結合される．であるから，ソート時間T[n]は中間を計算する一定の時間 b，各半分を計算する時間2T[n/2]，2つの半分を結合するための要素数の倍数 a n の合計になる：

再帰方程式を解いて n 個の要素をソートする時間 t を求める：

であり，したがってこのアルゴリズムのランタイムがであることを示す：

シュトラッセン(Strassen)のアルゴリズムは，はじめて求まったSubcubic行列の乗法アルゴリズムである．このアルゴリズムは，2つの行列のそれぞれをサイズが等しい4つの部分行列に分割し，8つの部分行列から14個の特定の線形結合を形成し，これらの7対の乗算を行なって，7つの結果の線形結合を形成する，という4ステップからなる．乗算を行う時間は，したがって，行列を分割する固定時間，2番目と4番目の線形結合を形成する時間，第3ステップのである：

再帰関係を解く：

結果は複雑ではあるが，と漸近的に等しい：

ナイーブな立方アルゴリズムとシュトラッセンのアルゴリズムの成長率を比較する：

収束判定法 (2)

$sum_(n=1)^inftyTemplateBox[{{a, _, n}}, Abs]<infty$ であれば，列は絶対加算可能であると言われる．第2列がなら，比較判定法は，が絶対加算可能であるときかつそのときに限りみも絶対加算可能であると述べる．この判定法を使って，総和と比較することによってが収束することを示す：

SumConvergenceが与える答と比較する：

の総和と比較することでが収束することを示す：

の総和と比較することでが発散することを示す：

SumConvergenceが与える答と比較する：

列は，したがって，絶対加算可能ではない：

$int_a^bTemplateBox[{{f, , {(, x, )}}}, Abs]dx<infty$ ならば，関数はに対して完全に積分可能であると言われる．とが開区間で連続的であり，との両方でなら，比較判定法はが完全に積分可能であるときかつそのときに限りもそうであるとする．この判定法を使ってがで完全に積分可能であることを示す：