BinLists

BinLists[data]

gives lists of the elements of data whose values lie in successive integer bins.

BinLists[data,binspec]

gives lists of the elements of data whose values lie in successive bins specified by binspec.

BinLists[datainds,…]

gives the lists of the labels inds specified by the binning of data.

Details

  • BinLists drops elements whose values do not correspond to real numbers.
  • The following bin-width specifications binspec can be given:
  • dxbins of width dx »
    {xmin,xmax,dx}bins of width dx from xmin to xmax »
    {{b1,b2,…}}the intervals [b1,b2), [b2,b3), … »
    xbins,ybins,…bin specifications for multivariate data understood as {{x1,y1,…},{x2,y2, …},…} »
  • BinLists[data,dx] takes the bin boundaries to be integer multiples of dx, with the first bin starting at Ceiling[Min[data]-dx,dx] and the last bin ending at Floor[Max[data]+dx,dx].
  • BinLists[data] is equivalent to BinLists[data,1].
  • In BinLists[data,{xmin,xmax,dx}], elements are placed in bin i when their values satisfy .
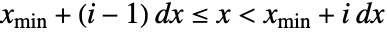
  • BinLists[data,{xmin,xmax}] is equivalent to BinLists[data,{xmin,xmax,1}].
  • In BinLists[data,{{b1,b2,…}}], elements are put in bin i when their values satisfy .
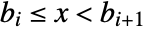
  • In the form BinLists[data,{{b1,b2,…}}], the bi at each end can be -Infinity and +Infinity.
  • If the bi do not form an increasing sequence, they are automatically sorted by BinLists.
  • If data consists of length-n sublists, then n bin specifications must be given, and BinLists[data,…] yields an array of lists of depth n.
  • Within each bin, elements appear in the same order as in the original data.
  • The data can have the following forms and interpretations:
  • {x1,x2,…}list of real numbers or quantities »
    {{x1,y1,…},{x2,y2,…},…}list of vectors of the same dimension »
    SparseArrayan array equivalent to Normal[data] »
    QuantityArrayarray of column-compatible quantities »
    TimeSeries, TemporalData,…vector or array of values (the time stamps ignored) »
  • Labels inds for the input elements xi can be given in the following formats: »
  • {x1,x2,…}use the xi themselves (no labels by default)
    {x1,x2,…}Automaticuse integer labels
    {x1,x2,…}{v1,v2,…}a rule between all the elements and all the labels
    {x1v1,x2v2,…}a list of rules between the element xi and its label vi

Examples

open allclose all

Basic Examples  (3)

List elements in bins of a specified width:

Make lists of elements in bins of width 1 from 0 to 10:

List elements in a sequence of ranges:

Scope  (12)

Basic Uses  (8)

List squares mod 3 and 5 in two-dimensional unit bins:

List random pairs in bins of width 0.25 in both dimensions:

List multidimensional data in ranges:

Bin data in any dimension:

Bin data, ignoring values that are not real:

Bin data of any precision:

SparseArray data can be used just like dense arrays:

Bin data from a time series:

The time stamps are ignored:

Data with Quantities  (3)

Bin quantity data:

Automatic bins:

Specify bin width:

Bins of fixed width, minimum and maximum:

Specify bin intervals:

Bin mixed-type data:

The units are compatible for each dimension:

Specify bin width for each dimension:

QuantityArray can be used just like arrays:

Automatic bins:

Specify bin width in compatible units:

Data with Labels  (1)

Bin data with output as an array of labels:

Bin data with default integer labels:

Applications  (1)

Visualize two-dimensional data in bins:

Properties & Relations  (1)

The length of BinLists is equivalent to the results from BinCounts:

For a list of vectors:

Possible Issues  (4)

Binning intervals are closed on the left:

For data involving quantities, the bin specification must be given in compatible units:

Matrix data must have unit-compatible columns:

The bins obtained using the specification {min,max,dx} may not include all data points:

Specify the min and max so all data points are included in the bin covering:

Alternatively, use the width-only bin specification dx:

Wolfram Research (2007), BinLists, Wolfram Language function, https://reference.wolfram.com/language/ref/BinLists.html (updated 2024).

Text

Wolfram Research (2007), BinLists, Wolfram Language function, https://reference.wolfram.com/language/ref/BinLists.html (updated 2024).

CMS

Wolfram Language. 2007. "BinLists." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/BinLists.html.

APA

Wolfram Language. (2007). BinLists. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BinLists.html

BibTeX

@misc{reference.wolfram_2025_binlists, author="Wolfram Research", title="{BinLists}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/BinLists.html}", note=[Accessed: 29-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_binlists, organization={Wolfram Research}, title={BinLists}, year={2024}, url={https://reference.wolfram.com/language/ref/BinLists.html}, note=[Accessed: 29-May-2025 ]}