WOLFRAM

Wolfram 语言与系统参考资料中心

CanonicalizePolygon[poly]

给出多边形 poly 的标准表示，其中包含共享坐标和内外边界.

CanonicalizePolygon[poly,"filter"]

给出 poly 的经过指定“过滤器”的标准表示.

更多信息
Details and Options Details and Options
范例  
基本范例  
范围  
基本用法  
规范  
应用  
属性和关系  
可能存在的问题  
参见
相关指南
历史
按以下格式引用：

CanonicalizePolygon

CanonicalizePolygon[poly]

给出多边形 poly 的标准表示，其中包含共享坐标和内外边界.

CanonicalizePolygon[poly,"filter"]

给出 poly 的经过指定“过滤器”的标准表示.

更多信息

  • CanonicalizePolygon 用于从各种表示和描述中获取多边形的简单标准表示.
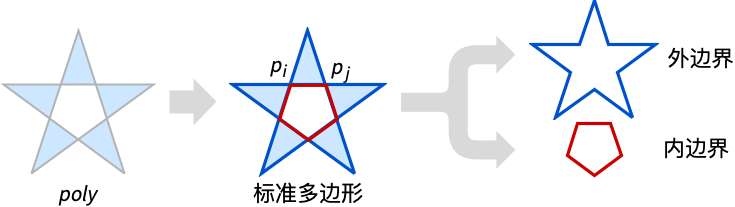
  • CanonicalizePolygon 将多边形转换为最优的标准形式 Polygon[{p1,p2,…},{outer1,outer2inner2,…}].
  • 点 pi 是非交叉线段的端点，并按 Sort 顺序排序.
  • 外边界 outerk 是一个由线段 {pi,pj} 组成的闭合曲线，可能在端点相接但没有其他交叉点.
  • 内边界 innerk 是一个由线段 {pi,pj} 组成的闭合曲线，可能在端点相接但没有其他交叉点.
  • 广义的多边形规范可以给出表示线和点的退化多边形. 通过使用 "filter" 规范，可以控制是否保留这些低维部分.
  • 可能的 "filter" 规范包括：
  • All所有组件，包括线和点
    Full只保留全维部分

范例

打开所有单元 关闭所有单元

基本范例  (1)

给出 Polygon 的标准形式：

Wolfram Language code: 𝒫 = Polygon[{{1, 0}, {0, Sqrt[3]}, {-1, 0}}];
Wolfram Language code: CanonicalizePolygon[𝒫]
Wolfram Language code: Graphics[%]

范围  (9)

基本用法  (7)

CanonicalizePolygon 适用于多边形：

Wolfram Language code: Polygon[{{0, 0}, {1., 0.}, {0.5, 1}}];
Wolfram Language code: CanonicalizePolygon[%]

三角形：

Wolfram Language code: CanonicalizePolygon[Triangle[]]

长方形：

Wolfram Language code: CanonicalizePolygon[Rectangle[]]

有洞的多边形：

Wolfram Language code: Polygon[{{0, 0}, {3, 0}, {3, 3}, {0, 3}, {1, 1}, {1, 2}, {2, 2}, {2, 1}}, {1, 2, 3, 4} -> {{5, 6, 7, 8}}];
Wolfram Language code: CanonicalizePolygon[%]

CanonicalizePolygon 适用于具有地理实体的多边形：

Wolfram Language code: CanonicalizePolygon[Polygon[["france"]]]

具有 GeoPosition 的多边形：

Wolfram Language code: Polygon[GeoPosition[{{{40.083441, -88.235716}, {40.083607, -88.257488}, {40.082603, -88.257149}, {40.076136999999996, -88.25740499999999}, {40.076178, -88.270888}, {40.076516, -88.271558}, {40.083686, -88.271512}, {40.083659999999995, -88.267046}, ... 33323}, {40.098112, -88.228687}, {40.095216, -88.228627}, {40.095179, -88.238547}, {40.094480999999995, -88.238546}, {40.094508999999995, -88.23267}, {40.094106, -88.232556}, {40.090666999999996, -88.232477}, {40.090741, -88.235745}}}]];
Wolfram Language code: CanonicalizePolygon[%]

具有 GeoPositionXYZ 的多边形：

Wolfram Language code: Polygon[GeoPositionXYZ[{{{150451.6968462432, -4.884430486484052*^6, 4.085078564164219*^6}, {148595.27532671497, -4.884475441490381*^6, 4.085092666620835*^6}, {148626.35829777512, -4.884546311005128*^6, 4.0850073717259285*^6}, {148618.5908634042 ... 7*^6, 4.0860187668081024*^6}, {150697.56410771207, -4.8836599487428395*^6, 4.085984535480795*^6}, {150711.88303095422, -4.883905546449982*^6, 4.0856924143435075*^6}, {150433.15479548014, -4.883908845676418*^6, 4.0856987003255524*^6}}}]];
Wolfram Language code: CanonicalizePolygon[%]

具有 GeoPositionENU 的多边形：

Wolfram Language code: Polygon[GeoPositionENU[{{{3378.2547059731055, -3369.2234780923936, -0.7440009205072329}, {1521.3211635380246, -3351.391253626573, -0.022340134218666208}, {1550.2571145363192, -3462.8657556618973, -0.08899812728964207}, {1528.5672303494055, -418 ... 63383291193, -0.37494203351275246}, {3654.121991908476, -2566.7472331234085, -0.5214977847472255}, {3375.420726854886, -2558.6597093173914, -0.3648706331350695}}}, GeoPosition[{40.11379115639895, -88.2753251202516, -1.0415787873318691}]]];
Wolfram Language code: CanonicalizePolygon[%]

具有 GeoGridPosition 的多边形：

Wolfram Language code: Polygon[GeoGridPosition[{{{-0.9950503945490105, 1.2366760550756015}, {-0.9952074890903578, 1.2369207053693891}, {-0.9952196732768064, 1.2369073327446167}, {-0.9953160063787643, 1.236848436956935}, {-0.9954141759436825, 1.2369993898475449}, {-0. ... 197645333103}, {-0.9949098578570917, 1.2368130881428654}, {-0.9948663952535768, 1.2367477711687371}, {-0.9948714472169538, 1.2367426500757825}, {-0.9949211061652593, 1.2367089232486177}, {-0.9949439717990124, 1.236746107097628}}}, "Bonne"]];
Wolfram Language code: CanonicalizePolygon[%]

自相交的多边形：

Wolfram Language code: Polygon[{{0.35, 0.2}, {0.9, 0.75}, {0.1, 0.55}, {0.9, 0.35}, {0.42, 0.9}}];
Wolfram Language code: CanonicalizePolygon[%]

组件不相连的多边形：

Wolfram Language code: Polygon[{{0, 0}, {1, 0}, {0, 1}, {1, 1}, {2, 1}, {1, 2}}, {{1, 2, 3}, {4, 5, 6}}];
Wolfram Language code: CanonicalizePolygon[%]

中的多边形：

Wolfram Language code: Polygon[{{2, 3, 1, 0}, {6, 9, 1, 0}, {5, 4, 1, 0}, {8, 2, 1, 0}}, {1, 2, 3, 4}];
Wolfram Language code: CanonicalizePolygon[%]

规范  (2)

给出多边形的所有组件：

Wolfram Language code: 𝒫 = Polygon[{{{1, 0}, {0, Sqrt[3]}, {-1, 0}}, {{2, 2}, {3, 3}}}]
Wolfram Language code: CanonicalizePolygon[𝒫, All]

给出多边形的全维组件：

Wolfram Language code: 𝒫 = Polygon[{{{1, 0}, {0, Sqrt[3]}, {-1, 0}}, {{2, 2}, {3, 3}}}]
Wolfram Language code: CanonicalizePolygon[𝒫, Full]

应用  (2)

设置一个共享坐标的图形复合体:

Wolfram Language code: 𝒞𝒫 = CanonicalizePolygon[Polygon[{{{0, 0, 0}, {2, 0, 0}, {1, 1, 2}}, {{2, 0, 0}, {2, 2, 0}, {1, 1, 2}}, {{2, 2, 0}, {0, 2, 0}, {1, 1, 2}}, {{0, 2, 0}, {0, 0, 0}, {1, 1, 2}}}]]
Wolfram Language code: Graphics3D[{GraphicsComplex[𝒞𝒫[[1]], Polygon[𝒞𝒫[[2]]]]}]

求给定线段的自交点：

Wolfram Language code: seg = {{-0.6, -0.8}, {0.9, 0.3}, {-0.9, 0.3}, {0.6, -0.8}, {0., 1.}, {-0.6, -0.8}};
Wolfram Language code: coords = CanonicalizePolygon[Polygon[seg]][[1]];
Wolfram Language code: intersection = Complement[coords, seg];
Wolfram Language code: Graphics[{Line[seg], PointSize[Medium], Red, Point[intersection], Blue, Point[seg]}]

属性和关系  (4)

使用 CanonicalizePolygon 获取 PolygonCoordinates：

Wolfram Language code: 𝒫 = Polygon[{{1, 0}, {0, Sqrt[3]}, {-1, 0}}];
Wolfram Language code: First[CanonicalizePolygon[𝒫]]
Wolfram Language code: PolygonCoordinates[𝒫]

简单多边形的 CanonicalizePolygon 保留多边形坐标数：

Wolfram Language code: 𝒫 = Polygon[{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}];
Wolfram Language code: SimplePolygonQ[𝒫]
Wolfram Language code: Length[First[#]]& /@ {𝒫, CanonicalizePolygon[𝒫]}

OuterPolygon 给出外多边形的标准表示：

Wolfram Language code: OuterPolygon[Polygon[{{0.35, 0.2}, {0.9, 0.75}, {0.1, 0.55}, {0.9, 0.35}, {0.42, 0.9}}]]

InnerPolygon 给出内多边形的标准表示：

Wolfram Language code: InnerPolygon[Polygon[{{0.35, 0.2}, {0.9, 0.75}, {0.1, 0.55}, {0.9, 0.35}, {0.42, 0.9}}]]

可能存在的问题  (1)

CanonicalizePolygon 只适于几何区域：

Wolfram Language code: 𝒫 = Polygon[{{0, 0, 0}, {1, 1, 0}, {0, 1, 0}, {0, 0, 1}}];
Wolfram Language code: {CanonicalizePolygon[𝒫], RegionQ[𝒫]}
Wolfram Research (2019)，CanonicalizePolygon，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CanonicalizePolygon.html.

文本

Wolfram Research (2019)，CanonicalizePolygon，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CanonicalizePolygon.html.

CMS

Wolfram 语言. 2019. "CanonicalizePolygon." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CanonicalizePolygon.html.

APA

Wolfram 语言. (2019). CanonicalizePolygon. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CanonicalizePolygon.html 年

BibTeX

@misc{reference.wolfram_2026_canonicalizepolygon, author="Wolfram Research", title="{CanonicalizePolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/CanonicalizePolygon.html}", note=[Accessed: 22-June-2026]}

BibLaTeX

@online{reference.wolfram_2026_canonicalizepolygon, organization={Wolfram Research}, title={CanonicalizePolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/CanonicalizePolygon.html}, note=[Accessed: 22-June-2026]}