WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

WindingPolygon
✖
WindingPolygon

✖
WindingPolygon[{p1,p2,…,pn}]

gives a polygon representing all points for which the closed contour p1,p2,…,pn,p1 winds around at least once.

✖
WindingPolygon[{{p11,p12,…},{p21,p22,…},…}]

gives a polygon from the closed contours p11,p12,… and p21,p22,….

✖
WindingPolygon[…,"wrule"]

uses the specified winding rule "wrule" to define the polygon.

Details and Options

  • WindingPolygon is also known as winding filling rule.
  • WindingPolygon is commonly used to define a polygon from self-intersecting closed curves.
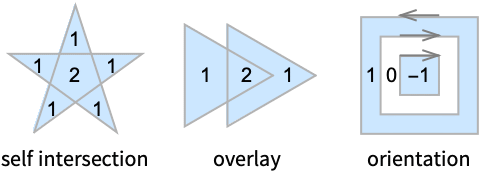
  • A point p is in the polygon if the number of revolutions of the closed contour around p is not zero. The number of revolutions is given by WindingCount.
  • The number of winding counts are given below for each region:
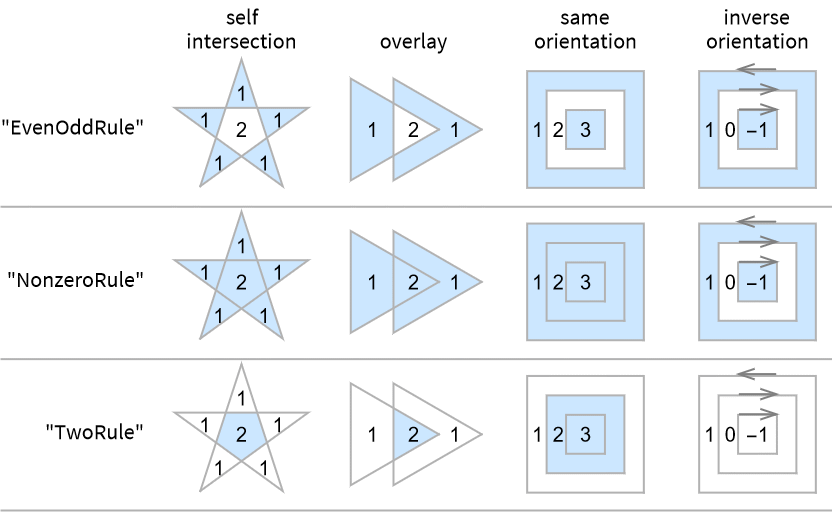
  • Different winding rules "wrule" give different polygons. Possible winding rules include:
  • WindingPolygon[{p1,p2,…}] is equivalent to WindingPolygon[{p1,p2,…},"NonzeroRule"].
  • The points pi can have any embedding dimension, but must all lie in a plane and have the same embedding dimension.
  • WindingPolygon takes the same options as Polygon.

    • List of all options

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Define a polygon:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-p3b1a8
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-it4riy
Out[2]=2

Construct a polygon from a self-intersecting contour:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-ihjkg4
Out[1]=1

Its area:

In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-qdev09
Out[2]=2

Scope  (14)Survey of the scope of standard use cases

Basic Uses  (5)

Define a two-dimensional polygon:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-6wznbi
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-k7h2jz
Out[2]=2

Three-dimensional polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-d5b3jx
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-zl0rxy
Out[2]=2

n-dimensional polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-tto0a3
Out[1]=1

Construct polygons from self-intersecting contours:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-tgsruf
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-5pmab3
Out[2]=2

Multiple contours:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-z2w99s
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-pageqd
Out[2]=2

Nonzero Rule  (3)

Polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-hkfe8s
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-7sdo6l
Out[2]=2

Three-dimensional polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-nwkw0d
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-cz4s4c
Out[2]=2

n-dimensional polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-r2012o
Out[1]=1

EvenOdd Rule  (3)

Polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-iq6flg
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-u2y9kk
Out[2]=2

Three-dimensional polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-emp4sz
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-mj7qx7
Out[2]=2

n-dimensional polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-53u2au
Out[1]=1

Two Rule  (3)

Polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-9p0fmk
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-2n139l
Out[2]=2

Three-dimensional polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-h7cau
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-ddzc0m
Out[2]=2

n-dimensional polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-ikf7sy
Out[1]=1

Options  (6)Common values & functionality for each option

VertexColors  (2)

Polygon with vertex colors:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-emgyge
Out[1]=1

Specify vertex colors for 3D polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-2k04y9
Out[1]=1

VertexNormals  (1)

Compute normal vectors using the cross-product of edge vectors:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-lx25c
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-bpd9f0
Out[2]=2

A triangle with normals pointing in the direction {1,-1,1}:

In[3]:=3
✖
https://wolfram.com/xid/0b0l38rewmi-cvwg32
Out[3]=3

Using different normals will affect shading:

In[4]:=4
✖
https://wolfram.com/xid/0b0l38rewmi-dxgk6r
Out[4]=4

VertexTextureCoordinates  (3)

Texture mapping with 2D polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-1jlxp
Out[1]=1

Texture mapping with 3D polygons:

In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-eg1zja
Out[2]=2

Repeat a texture by using non-unified texture coordinate values:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-drfwj5
Out[1]=1

Texture mapping is preceded by VertexColors:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-ew2q5d
Out[1]=1

Applications  (3)Sample problems that can be solved with this function

Basic Applications  (1)

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-f0eecn
Out[1]=1

Geometry  (1)

Generation of regular star polygons:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-32sy0l
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-lbxtsa
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b0l38rewmi-lvckt4
Out[3]=3

Computational Geometry  (1)

Generate random polygons:

In[3]:=3
✖
https://wolfram.com/xid/0b0l38rewmi-x3b685
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0b0l38rewmi-hz73c1
Out[4]=4

Properties & Relations  (2)Properties of the function, and connections to other functions

WindingPolygon is in general different than Polygon:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-hf6fz3
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-c82bc3
Out[2]=2

CrossingPolygon is an alternate polygon constructor:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-0h89de
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-14smh2
Out[2]=2

Possible Issues  (2)Common pitfalls and unexpected behavior

WindingPolygon always gives full-dimensional components:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-gs2kxl
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0l38rewmi-xtcaug
Out[2]=2

The points in WindingPolygon must lie on a plane:

In[1]:=1
✖
https://wolfram.com/xid/0b0l38rewmi-4o4cqe
Out[1]=1
Wolfram Research (2019), WindingPolygon, Wolfram Language function, https://reference.wolfram.com/language/ref/WindingPolygon.html.
✖
Wolfram Research (2019), WindingPolygon, Wolfram Language function, https://reference.wolfram.com/language/ref/WindingPolygon.html.

Text

Wolfram Research (2019), WindingPolygon, Wolfram Language function, https://reference.wolfram.com/language/ref/WindingPolygon.html.

✖
Wolfram Research (2019), WindingPolygon, Wolfram Language function, https://reference.wolfram.com/language/ref/WindingPolygon.html.

CMS

Wolfram Language. 2019. "WindingPolygon." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WindingPolygon.html.

✖
Wolfram Language. 2019. "WindingPolygon." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WindingPolygon.html.

APA

Wolfram Language. (2019). WindingPolygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WindingPolygon.html

✖
Wolfram Language. (2019). WindingPolygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WindingPolygon.html

BibTeX

@misc{reference.wolfram_2025_windingpolygon, author="Wolfram Research", title="{WindingPolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/WindingPolygon.html}", note=[Accessed: 05-May-2025 ]}

✖
@misc{reference.wolfram_2025_windingpolygon, author="Wolfram Research", title="{WindingPolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/WindingPolygon.html}", note=[Accessed: 05-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_windingpolygon, organization={Wolfram Research}, title={WindingPolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/WindingPolygon.html}, note=[Accessed: 05-May-2025 ]}

✖
@online{reference.wolfram_2025_windingpolygon, organization={Wolfram Research}, title={WindingPolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/WindingPolygon.html}, note=[Accessed: 05-May-2025 ]}