CrossingPolygon[{p1,p2,…,pn}]
gives a Polygon representing all points for which a ray from the point in any direction in the plane crosses the line segments {p1,p2},…,{pn-1,pn},{pn,p1} an odd number of times.
CrossingPolygon[{{p11,p12,…},{p21,p22,…},…}]
gives a Polygon from the line segments {p11,p12},…,{p21,p22},….


CrossingPolygon
CrossingPolygon[{p1,p2,…,pn}]
gives a Polygon representing all points for which a ray from the point in any direction in the plane crosses the line segments {p1,p2},…,{pn-1,pn},{pn,p1} an odd number of times.
CrossingPolygon[{{p11,p12,…},{p21,p22,…},…}]
gives a Polygon from the line segments {p11,p12},…,{p21,p22},….
Details and Options

- CrossingPolygon is also known as even–odd filling rule.
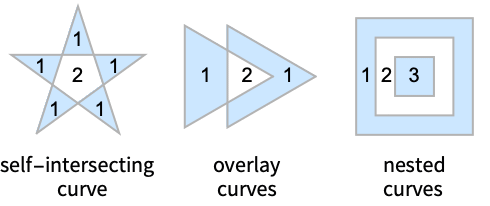
- A point is in CrossingPolygon if a ray starting at that point to infinity in any direction will cross the boundary curves an odd number of times. The number of ray crossings is given by CrossingCount.
- The number of ray crossings is given below for each region.
- CrossingPolygon is used to define a polygon from possibly self-intersecting closed curves.
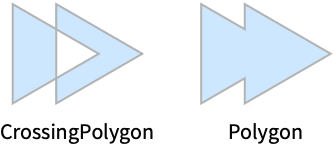
- CrossingPolygon[{p1,p2,…,pn}] is effectively equivalent to Polygon[{p1,p2,…,pn}].
- CrossingPolygon[{{p11,p12,…},{p21,p22,…},…}] is, in general, different than Polygon[{{p11,p12,…},{p21,p22,…},…}] since the former will use the ray crossing rule for all closed curves {pi1,pi2,…}. The latter is the union of polygons Polygon[{pi1,pi2,…}].
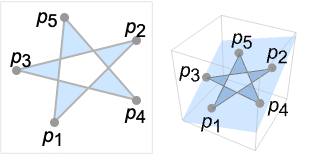
- The points pi can have any length but must all lie in a plane.
- CrossingPolygon takes the same options as Polygon.
List of all options
Examples
open all close allBasic Examples (2)
Scope (11)
Basic Uses (5)
Self-Intersecting Contours (3)
CrossingPolygon works on self-intersecting contours:
Multiple Contours (3)
Options (6)
VertexNormals (1)
VertexTextureCoordinates (3)
Texture mapping with 2D polygons:
Texture mapping with 3D polygons:
Repeat a texture by using non-unified texture coordinate values:
Texture mapping is preceded by VertexColors:
Applications (3)
Properties & Relations (3)
CrossingPolygon is effectively equivalent to Polygon for a single contour:
CrossingPolygon is, in general, different than Polygon for multiple intersecting contours:
WindingPolygon is an alternate polygon constructor:
Possible Issues (1)
The points in CrossingPolygon must all lie on a plane:
Related Guides
History
Text
Wolfram Research (2019), CrossingPolygon, Wolfram Language function, https://reference.wolfram.com/language/ref/CrossingPolygon.html.
CMS
Wolfram Language. 2019. "CrossingPolygon." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CrossingPolygon.html.
APA
Wolfram Language. (2019). CrossingPolygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CrossingPolygon.html
BibTeX
@misc{reference.wolfram_2025_crossingpolygon, author="Wolfram Research", title="{CrossingPolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/CrossingPolygon.html}", note=[Accessed: 02-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_crossingpolygon, organization={Wolfram Research}, title={CrossingPolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/CrossingPolygon.html}, note=[Accessed: 02-March-2026]}