CarlsonRJ

CarlsonRJ[x,y,z,ρ]

gives Carlson's elliptic integral TemplateBox[{x, y, z, rho}, CarlsonRJ].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • For non-negative arguments, TemplateBox[{x, y, z, rho}, CarlsonRJ]⩵3/2int_0^infty(t+x)^(-1/2)(t+y)^(-1/2)(t+z)^(-1/2)(t+rho)^(-1)dt.
  • CarlsonRJ[x,y,z,ρ] has a branch cut discontinuity at .
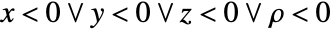  • CarlsonRJ[x,y,z,ρ] is understood as a Cauchy principal value integral for .
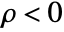  • For certain arguments, CarlsonRJ automatically evaluates to exact values.
  • CarlsonRJ can be evaluated to arbitrary precision.
  • CarlsonRJ automatically threads over lists.
  • CarlsonRJ can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (3)

Evaluate numerically:

Visualize over a range of arguments:

CarlsonRJ is related to the Legendre elliptic integral of the third kind TemplateBox[{n, phi, m}, EllipticPi3] for :

Scope  (14)

Numerical Evaluation  (6)

Evaluate numerically:

Evaluate at high precision:

Precision of the output tracks the precision of the input:

Evaluate for complex arguments:

Evaluate efficiently at high precision:

CarlsonRJ threads elementwise over lists:

CarlsonRJ can be used with Interval and CenteredInterval objects:

Specific Values  (3)

Simple exact values are generated automatically:

When one of the first three arguments of CarlsonRJ is zero, CarlsonRJ reduces to the complete elliptic integral CarlsonRM:

When one of the first three arguments of CarlsonRJ is equal to the last argument, and they do not lie on the negative real axis, CarlsonRJ reduces to CarlsonRD:

Differentiation and Integration  (2)

Derivative of TemplateBox[{x, y, z, rho}, CarlsonRJ] with respect to :

Derivative of TemplateBox[{x, y, z, rho}, CarlsonRJ] with respect to :

Indefinite integral of TemplateBox[{x, y, z, rho}, CarlsonRJ] with respect to :

Function Representations  (1)

TraditionalForm formatting:

Function Identities and Simplifications  (2)

CarlsonRJ satisfies the Euler–Poisson partial differential equation:

CarlsonRJ satisfies Euler's homogeneity relation:

Applications  (1)

Use CarlsonRJ to define a conformal map:

Visualize the image of lines of constant real and imaginary parts:

Properties & Relations  (2)

CarlsonRJ is invariant under a permutation of its first three arguments:

Verify the change of parameter relation for CarlsonRJ:

Wolfram Research (2021), CarlsonRJ, Wolfram Language function, https://reference.wolfram.com/language/ref/CarlsonRJ.html (updated 2023).

Text

Wolfram Research (2021), CarlsonRJ, Wolfram Language function, https://reference.wolfram.com/language/ref/CarlsonRJ.html (updated 2023).

CMS

Wolfram Language. 2021. "CarlsonRJ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/CarlsonRJ.html.

APA

Wolfram Language. (2021). CarlsonRJ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CarlsonRJ.html

BibTeX

@misc{reference.wolfram_2024_carlsonrj, author="Wolfram Research", title="{CarlsonRJ}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/CarlsonRJ.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_carlsonrj, organization={Wolfram Research}, title={CarlsonRJ}, year={2023}, url={https://reference.wolfram.com/language/ref/CarlsonRJ.html}, note=[Accessed: 18-November-2024 ]}