CarmichaelLambda

CarmichaelLambda[n]

gives the Carmichael function .

Details

  • CarmichaelLambda is also known as the reduced totient function or the least universal exponent function.
  • CarmichaelLambda is typically used in primality testing to find a composite number that cannot be proved composite by some primality tests.
  • Integer mathematical function, suitable for both symbolic and numerical manipulation.
  • CarmichaelLambda[n] is the smallest positive integer 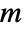such that 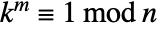for all 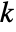relatively prime to .
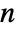  • For a number 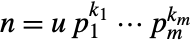with 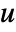a unit and 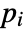primes, CarmichaelLambda[n] returns LCM[(p1-1)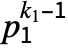,…,(pm-1)].

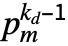Examples

open allclose all

Basic Examples  (2)

Compute CarmichaelLambda of :

Plot the sequence:

Scope  (7)

Numerical Evaluation  (4)

Compute using integers:

Compute for large integers:

CarmichaelLambda threads over lists:

TraditionalForm formatting:

Symbolic Manipulation  (3)

Find an integer solution instance:

Simplify an expression:

Identify the CarmichaelLambda sequence:

Applications  (7)

Basic Applications  (3)

The first 20 values of CarmichaelLambda:

Discrete plot:

Number line plot:

Plot the generating function:

Exponential generating function:

Dirichlet series:

Primality Testing  (2)

Given a prime, for all positive numbers a less than p:

A natural test for primality:

This test can be inconclusive for composite integers n satisfying :

Verify for all a coprime to 561:

Recognize Carmichael numbers, composite numbers with an≡1 mod n for all a coprime to n:

The number is a Carmichael number, is not:

Cryptography  (1)

Build RSA-like encryption scheme. Start with the modulus:

Find the universal exponent of the multiplication group modulo n:

Private key:

Public key:

Encrypt a message:

Decrypt it:

Number Theory  (1)

Find the number of elements in the largest subgroup of Z_n^*:

Properties & Relations  (7)

The result is non-negative:

Divisibility is preserved:

The LCM of CarmichaelLambda is equal to CarmichaelLambda of the LCM:

If is square-free then a≡aλ(n)+1mod n:

The multiplicative order of an element modulo divides CarmichaelLambda[n]:

CarmichaelLambda divides EulerPhi:

If has a primitive root, then CarmichaelLambda and EulerPhi are the same:

Neat Examples  (2)

A plot of varying CarmichaelLambda values:

Ulam spiral where numbers are colored based on the values of CarmichaelLambda:

Wolfram Research (1999), CarmichaelLambda, Wolfram Language function, https://reference.wolfram.com/language/ref/CarmichaelLambda.html (updated 2018).

Text

Wolfram Research (1999), CarmichaelLambda, Wolfram Language function, https://reference.wolfram.com/language/ref/CarmichaelLambda.html (updated 2018).

CMS

Wolfram Language. 1999. "CarmichaelLambda." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2018. https://reference.wolfram.com/language/ref/CarmichaelLambda.html.

APA

Wolfram Language. (1999). CarmichaelLambda. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CarmichaelLambda.html

BibTeX

@misc{reference.wolfram_2024_carmichaellambda, author="Wolfram Research", title="{CarmichaelLambda}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/CarmichaelLambda.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_carmichaellambda, organization={Wolfram Research}, title={CarmichaelLambda}, year={2018}, url={https://reference.wolfram.com/language/ref/CarmichaelLambda.html}, note=[Accessed: 22-November-2024 ]}