CarmichaelLambda

CarmichaelLambda[n]

カーマイケル(Carmichael)関数 を与える．

詳細

  • CarmichaelLambdaは，簡約トーシェント関数あるいは最小普遍指数関数としても知られている．
  • CarmichaelLambdaは，素数判定で，ある種の素数判定では合成数であると証明できない合成数を求めるためによく使われる．
  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • CarmichaelLambda[n]は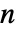， と互いに素であるすべての 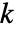について 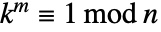となるような最小の正の整数 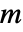である．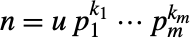
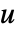  • （ は単数で 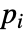は素数）について，CarmichaelLambda[n]はLCM[(p1-1)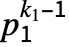,…,(pm-1)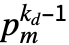]を返す．

例題

すべて開くすべて閉じる

例  (2)

のCarmichaelLambdaを計算する：

数列をプロットする：

スコープ  (7)

数値評価  (4)

整数を使って計算する：

大きい整数について計算する：

CarmichaelLambdaはリストに縫い込まれる：

TraditionalFormによる表示：

記号演算  (3)

整数の解の例を求める：

式を簡約する：

CarmichaelLambda数列を識別する：

アプリケーション  (7)

基本的なアプリケーション  (3)

CarmichaelLambdaの最初の20の値：

離散プロット：

数直線プロット：

母関数をプロットする：

指数母関数：

ディリクレ(Dirichlet)級数：

素数判定  (2)

素数が与えられた場合，p より小さいすべての正の数 a について である：

素数性についての自然なテスト：

このテストは を満足する合成整数 n に対しては結論が出せないかもしれない：

561と互いに素なすべての a について を検証する：

カーマイケル数，すなわち n と互いに素であるすべての a について an≡1 mod n である合成数を認識する：

はカーマイケル数だがは違う：

暗号学  (1)

RSAのような暗号スキームを構築する．まず，モジュラスから始める：

n を法とする乗法群の普遍指数を求める：

秘密鍵：

公開鍵：

メッセージを暗号化する：

これを解読する：

整数論  (1)

Z_n^*の最大部分群の元の数を求める：

特性と関係  (7)

結果は非負である：

被整除性は保持される：

CarmichaelLambdaのLCMはLCMのCarmichaelLambdaに等しい：

が無平方なら a≡aλ(n)+1mod n である：

を法とした元の乗法的位数はCarmichaelLambda[n]を割る：

CarmichaelLambdaはEulerPhiを割る：

が原始根を持つなら，CarmichaelLambdaとEulerPhiは等しい：

おもしろい例題  (2)

CarmichaelLambdaの値を変化させるプロット：

CarmichaelLambdaの値に基づいて数が彩色されたウラム(Ulam)螺線：

Wolfram Research (1999), CarmichaelLambda, Wolfram言語関数， https://reference.wolfram.com/language/ref/CarmichaelLambda.html （2018年に更新）.

テキスト

Wolfram Research (1999), CarmichaelLambda, Wolfram言語関数， https://reference.wolfram.com/language/ref/CarmichaelLambda.html （2018年に更新）.

CMS

Wolfram Language. 1999. "CarmichaelLambda." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2018. https://reference.wolfram.com/language/ref/CarmichaelLambda.html.

APA

Wolfram Language. (1999). CarmichaelLambda. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CarmichaelLambda.html

BibTeX

@misc{reference.wolfram_2024_carmichaellambda, author="Wolfram Research", title="{CarmichaelLambda}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/CarmichaelLambda.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_carmichaellambda, organization={Wolfram Research}, title={CarmichaelLambda}, year={2018}, url={https://reference.wolfram.com/language/ref/CarmichaelLambda.html}, note=[Accessed: 22-November-2024 ]}