CarmichaelLambda
给出卡迈克尔函数 ![]() .
.
更多信息

- CarmichaelLambda 也被称为简化欧拉函数或最小通用指数函数.
- CarmichaelLambda 通常在质数测试中使用,以查找无法通过某些质数测试证明为合数的合数.
- 整型数学函数,适合于符号和数值计算.
- CarmichaelLambda[n] 是最小的正整数
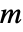 ,使得对于所有
,使得对于所有 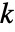 而言,
而言,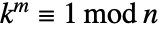 与
与 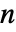 互质.
互质. - 对于数字
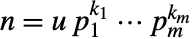 ,其中,
,其中,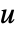 为单位值,
为单位值,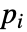 为素数,CarmichaelLambda[n] 返回 LCM[(p1-1)
为素数,CarmichaelLambda[n] 返回 LCM[(p1-1)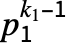 ,…,(pm-1)
,…,(pm-1)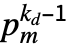 ].
].

范例
打开所有单元关闭所有单元基本范例 (2)
范围 (7)
数值运算 (4)
符号运算 (3)
应用 (7)
基本应用 (3)
素性测试 (2)
属性和关系 (7)
CarmichaelLambda 的 LCM 等于 LCM 的 CarmichaelLambda:
元素模除 ![]() 的乘法阶数整除 CarmichaelLambda[n]:
的乘法阶数整除 CarmichaelLambda[n]:
如果 ![]() 具有原根,则 CarmichaelLambda 和 EulerPhi 相同:
具有原根,则 CarmichaelLambda 和 EulerPhi 相同:
巧妙范例 (2)
Wolfram Research (1999),CarmichaelLambda,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CarmichaelLambda.html (更新于 2018 年).
文本
Wolfram Research (1999),CarmichaelLambda,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CarmichaelLambda.html (更新于 2018 年).
CMS
Wolfram 语言. 1999. "CarmichaelLambda." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2018. https://reference.wolfram.com/language/ref/CarmichaelLambda.html.
APA
Wolfram 语言. (1999). CarmichaelLambda. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CarmichaelLambda.html 年