CatalanNumber
给出了第 n![]() 个 卡塔兰数
个 卡塔兰数 ![]() .
.
更多信息
- CatalanNumber[n] 的一般定义为
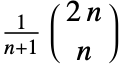 .
. - 对于整数参数,卡塔兰数为整数且出现在各种树状列举问题中.
- CatalanNumber 可与 Interval 和 CenteredInterval 对象一起使用: »
范例
打开所有单元关闭所有单元范围 (9)
计算涉及 CatalanNumber 的和:
CatalanNumber 按元素线性作用于列表:
CatalanNumber 可与 Interval 和 CenteredInterval 对象一起使用:
TraditionalForm 格式:
应用 (3)
分配到 CirclePlus 中的列表上:
卡塔兰数 CatalanNumber[n] 可描述为唯一一组使得两个汉克尔行列式都等于一的数字. 对前几种情况进行验证:
属性和关系 (6)
可以用 DifferenceRoot 来表示 CatalanNumber:
FindSequenceFunction 可以识别 CatalanNumber 序列:
CatalanNumber 的指数母函数:
巧妙范例 (2)
Wolfram Research (2007),CatalanNumber,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CatalanNumber.html (更新于 2014 年).
文本
Wolfram Research (2007),CatalanNumber,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CatalanNumber.html (更新于 2014 年).
CMS
Wolfram 语言. 2007. "CatalanNumber." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/CatalanNumber.html.
APA
Wolfram 语言. (2007). CatalanNumber. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CatalanNumber.html 年