CategoricalDistribution

CategoricalDistribution[{c1,c2,…}]

represents a uniform categorical distribution over classes c1, c2, etc.

CategoricalDistribution[{c1,c2,…},{w1,w2,…}]

represents a categorical distribution over classes ci with weights wi.

CategoricalDistribution[{{a1,a2,…},{b1,b2,…},…}]

represents a uniform multivariate categorical distribution over domain {a1,a2,…}×{b1,b2,…}×….

CategoricalDistribution[domain,weights]

uses the array weights to define probabilities over each element of the domain.

Details and Options

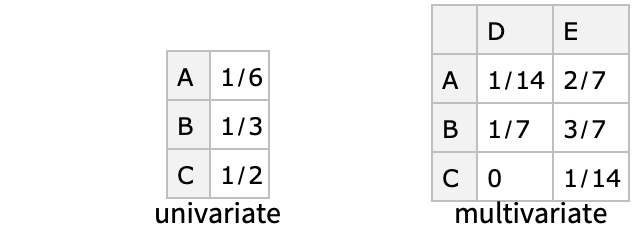
  • Categorical distribution is a discrete distribution whose domain is made of unordered classes (e.g. "A", "B", "C") and is typically used to give probability measures to finite collections of things.
  • Categorical distribution can have one or more variables. Probabilities for each domain element can be visualized in a contingency table:
  • CategoricalDistribution[…] can be used in functions such as RandomVariate, PDF, Probability and Expectation.
  • CategoricalDistribution[…] is not a numeric distribution: functions such as Mean or CDF cannot be used on it.
  • In CategoricalDistribution[domain,weights], the dimension of array weights must match the number of classes for each variable defined in domain.
  • Array weights can be given in a SparseArray[…] form.
  • When defined, weights are normalized to become probabilities.
  • CategoricalDistribution[{c1w1,c2w2,…}] can be used to define classes ci and weights wi.
  • CategoricalDistribution[{{c11,c12,…}w1,elem2w2,…}] can be used to define multivariate domain elements elemi (list of classes) and their weights wi. Omitted elements are given a 0 default weight.
  • In CategoricalDistribution[{elem1w1,elem2w2,…, _val}], omitted elements are given the weight val.
  • CategoricalDistribution[domain,{elem1w1,elem2w2,…}] can be used to specify both a distribution domain and probabilities for some domain elements.
  • Information[CategoricalDistribution[…]] gives a report about the distribution.
  • Information for CategoricalDistribution includes the following properties:
  • "Categories"list of distribution classes
    "Dimension"number of variables
    "DomainElements"all elements in the domain
    "DomainSize"number of elements in the domain
    "Entropy"exact entropy
    "NEntropy"approximate entropy
    "Probabilities"association of probabilities
    "ProbabilityArray"probability array
    "ProbabilityPlot"visualization of probability function
    "ProbabilityTable"probabilities in a Dataset
    "Properties"all available properties
    "TopProbabilities"list of elements with highest probabilities
    "TopProbabilities"ntop-n elements with highest probabilities

Examples

open allclose all

Basic Examples  (2)

Create a univariate and uniform categorical distribution:

Generate a random sample from the distribution:

Compute the probability mass of a class:

Create a weighted univariate categorical distribution:

Generate random samples from the distribution:

Compute the probability mass of classes:

Visualize the probabilities in a plot:

Scope  (15)

Univariate Definitions  (4)

Define a univariate categorical distribution with symbols as classes:

Generate samples from the distribution:

Define a univariate categorical distribution using rules:

Visualize information about the distribution:

Define a univariate categorical distribution using a domain and rules:

Visualize information about the distribution:

Specify default weights for undefined elements:

Visualize information about the distribution:

Define a categorical distribution with repeating elements:

Probabilities are proportional to the number of repeating elements:

Multivariate Definitions  (4)

Create a multivariate categorical distribution:

Generate random samples from the distribution:

Compute the probability mass of an element:

Visualize the contingency table of the distribution:

Compute the marginal distribution over the first variable:

Visualize the contingency table of the marginal distribution:

Define a multivariate categorical distribution using a sparse array:

Visualize its probability table:

Define a multivariate categorical distribution by defining a domain and rules:

Visualize its probability table:

Specify that undefined elements should have a given weight:

Visualize the probability table:

Create a categorical distribution with many variables:

Visualize its probability table:

Information  (2)

Create a univariate distribution:

Obtain an information report about the distribution:

Obtain a list of possible information properties:

Obtain the list of classes:

Obtain probabilities of all classes:

Visualize the probabilities:

Obtain the exact entropy of the distribution:

Create a multivariate distribution:

Obtain an information report about the distribution:

Obtain a list of possible information properties:

Obtain the possible classes for each variable:

Obtain all possible domain elements:

Obtain probabilities for all domain elements:

Obtain the elements that have the two highest probabilities:

Visualize the probabilities:

Obtain the exact entropy of the distribution:

Symbolic Weights  (2)

Define a categorical distribution with a symbolic (non-numeric) parameter:

Visualize the probability table:

Replace the parameter a with a numeric value:

Visualize the probability table:

Define a categorical distribution with a symbolic parameter:

RandomVariate does not evaluate:

Replace the symbolic parameter with a value:

Out-of-Domain Behavior  (1)

Define a categorical distribution:

The probability mass on "out-of-domain" classes is not defined, so PDF does not evaluate:

Replace the out-of-domain class with a domain class:

Probability & Expectation  (2)

Create a multivariate distribution:

Compute the probability that the first variable is "A":

Compare with the same probability computed with MarginalDistribution:

Create a multivariate distribution:

Compute its entropy using Expectation:

Compare with the entropy as given in Information:

Compute its entropy using NExpectation:

Specify that the "MonteCarlo" method should be used:

Specify the number of samples that should be used:

Applications  (2)

Train a classifier:

Return the predicted distribution for a given input:

Generate a random sample from the predicted distribution:

Load a dataset of passengers on the Titanic:

Extract three categorical variables and count their joined occurrences:

Create a categorical distribution from these counts:

Visualize the probability table of the distribution:

Compute the probability of surviving for a passenger:

Compute the probability of surviving for a female passenger:

Properties & Relations  (1)

Create a categorical distribution:

Obtain its probabilities for each element of the domain:

Probabilities are never negative:

Probabilities always sum to one:

Wolfram Research (2020), CategoricalDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/CategoricalDistribution.html.

Text

Wolfram Research (2020), CategoricalDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/CategoricalDistribution.html.

CMS

Wolfram Language. 2020. "CategoricalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CategoricalDistribution.html.

APA

Wolfram Language. (2020). CategoricalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CategoricalDistribution.html

BibTeX

@misc{reference.wolfram_2023_categoricaldistribution, author="Wolfram Research", title="{CategoricalDistribution}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CategoricalDistribution.html}", note=[Accessed: 19-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2023_categoricaldistribution, organization={Wolfram Research}, title={CategoricalDistribution}, year={2020}, url={https://reference.wolfram.com/language/ref/CategoricalDistribution.html}, note=[Accessed: 19-April-2024 ]}