NExpectation[expr,xdist]
gives the numerical expectation of expr under the assumption that x follows the probability distribution dist.
NExpectation[expr,{x1,x2,…}dist]
gives the numerical expectation of expr under the assumption that {x1,x2,…} follows the multivariate distribution dist.
NExpectation[expr,{x1dist1,x2dist2,…}]
gives the numerical expectation of expr under the assumption that x1, x2, … are independent and follow the distributions dist1, dist2, ….
NExpectation[exprpred,…]
gives the numerical conditional expectation of expr given pred.


NExpectation
NExpectation[expr,xdist]
gives the numerical expectation of expr under the assumption that x follows the probability distribution dist.
NExpectation[expr,{x1,x2,…}dist]
gives the numerical expectation of expr under the assumption that {x1,x2,…} follows the multivariate distribution dist.
NExpectation[expr,{x1dist1,x2dist2,…}]
gives the numerical expectation of expr under the assumption that x1, x2, … are independent and follow the distributions dist1, dist2, ….
NExpectation[exprpred,…]
gives the numerical conditional expectation of expr given pred.
Details and Options

- xdist can be entered as x
 dist
dist dist or x \[Distributed]dist.
dist or x \[Distributed]dist. - exprpred can be entered as expr
 cond
cond pred or expr \[Conditioned]pred.
pred or expr \[Conditioned]pred. - NExpectation works like Expectation, except numerical summation and integration methods are used.
- For a continuous distribution dist, the expectation of expr is given by
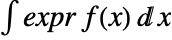 where
where 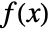 is the probability density function of dist and the integral is taken over the domain of dist.
is the probability density function of dist and the integral is taken over the domain of dist. - For a discrete distribution dist, the expectation of expr is given by
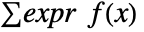 where
where 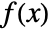 is the probability density function of dist and the summation is taken over the domain of dist.
is the probability density function of dist and the summation is taken over the domain of dist. - NExpectation[expr,{x1dist1,x2dist2}] corresponds to NExpectation[NExpectation[expr,x2dist2],x1dist1] so that the last variable is summed or integrated first.
- N[Expectation[…]] calls NExpectation for expectations that cannot be done symbolically.
- The following options can be given:
-
AccuracyGoal ∞ digits of absolute accuracy sought PrecisionGoal Automatic digits of precision sought WorkingPrecision MachinePrecision the precision used in internal computations Method Automatic what method to use TargetUnits Automatic units to display in the output
Examples
open all close allBasic Examples (3)
Scope (28)
Basic Uses (9)
Compute the expectation for an expression in a continuous univariate distribution:
Discrete univariate distribution:
Continuous multivariate distribution:
Discrete multivariate distribution:
Compute the expectation using independently distributed random variables:
Find the conditional expectation with general nonzero probability conditioning:
Discrete univariate distribution:
Multivariate continuous distribution:
Multivariate discrete distribution:
Compute the conditional expectation with a zero-probability conditioning event:
Apply N[Expectation[…]] to invoke NExpectation if symbolic evaluation fails:
Find the expectation of a rational function:
Obtain results with different precisions:
Compute an expectation for a time slice of a Poisson process:
Find the expectation of an expression when the distribution is specified by a list:
Quantity Uses (4)
Find expectation of quantity expressions:
Find expectations specified using QuantityDistribution:
Find conditional expectations:
Calculate expectation with QuantityMagnitude:
Parametric Distributions (4)
Nonparametric Distributions (2)
Using a univariate HistogramDistribution:
A multivariate histogram distribution:
Using a univariate KernelMixtureDistribution:
Derived Distributions (9)
Compute the expectation using a TransformedDistribution:
An equivalent way of formulating the same expectation:
Find the expectation using a ProductDistribution:
An equivalent formulation for the same expectation:
Using a component mixture of normal distributions:
Parameter mixture of exponential distributions:
Truncated Dirichlet distribution:
Censored triangular distribution:
Options (7)
AccuracyGoal (1)
Obtain a result with the default setting for accuracy:
Use AccuracyGoal to obtain the result with a different accuracy:
Method (3)
Use the Method option to increase the number of recursive bisections for numerical integration:
Compare with the exact result from Expectation:
Calculate the expectation for an expression:
Obtain an estimate based on simulation:
Calculate the expectation of an expression:
This example uses NIntegrate:
Use Activate to evaluate the result:
PrecisionGoal (1)
Obtain a result with the default setting for precision:
Use PrecisionGoal to obtain the result with a different precision:
WorkingPrecision (1)
By default, NExpectation uses machine precision:
Use WorkingPrecision to obtain results with higher precision:
TargetUnits (1)
Create a distribution object with quantity:
Expectation uses the quantity provided in the distribution as default:
Applications (17)
Distribution Properties (3)
Actuarial Science (4)
An insurance policy reimburses a loss up to a benefit limit of 10. The policyholder's loss, ![]() , follows a distribution with density function
, follows a distribution with density function ![]() for
for ![]() and 0 otherwise. Find the expected value of the benefit paid under the insurance policy:
and 0 otherwise. Find the expected value of the benefit paid under the insurance policy:
An insurance company's monthly claims are modeled by a continuous, positive random variable ![]() , whose probability density function is proportional to
, whose probability density function is proportional to ![]() where
where ![]() . Determine the company's expected monthly claims:
. Determine the company's expected monthly claims:
Claim amounts for wind damage to insured homes are independent random variables with common density function ![]() for
for ![]() and 0 otherwise, where
and 0 otherwise, where ![]() is the amount of a claim in thousands. Suppose 3 such claims will be made. Compute the expected value of the largest of the three claims:
is the amount of a claim in thousands. Suppose 3 such claims will be made. Compute the expected value of the largest of the three claims:
Let ![]() represent the age of an insured automobile involved in an accident. Let
represent the age of an insured automobile involved in an accident. Let ![]() represent the length of time the owner has insured the automobile at the time of the accident.
represent the length of time the owner has insured the automobile at the time of the accident. ![]() and
and ![]() have joint probability density function
have joint probability density function ![]() for
for ![]() and
and ![]() , and 0 otherwise. Calculate the expected age of an insured automobile involved in an accident:
, and 0 otherwise. Calculate the expected age of an insured automobile involved in an accident:
Sports (2)
Random Experiments (2)
Four six-sided dice are rolled. Find the expectation of the minimum value:
Find the expectation of the maximum value:
Find the expectation of the sum of the three largest values. Using the identity ![]() and linearity of Expectation, you get:
and linearity of Expectation, you get:
A random sample of size 10 from a continuous distribution ![]() is sorted in ascending order. A new random variate is generated. Find the probability that the 11
is sorted in ascending order. A new random variate is generated. Find the probability that the 11![]() sample falls between the fourth and fifth smallest values in the sorted list:
sample falls between the fourth and fifth smallest values in the sorted list:
Risk Analysis (2)
Study the tail value at risk (TVaR) for the exponential distribution:
Value at risk may underestimate possible losses. Consider two models for stock log-returns:
Fix parameter ![]() so that values at risk at the 99.5% level are equal:
so that values at risk at the 99.5% level are equal:
Now compute the expected losses in both models, given that they exceed the value at risk:
Other Applications (4)
A drug has proven to be effective in 40% of cases. Find the expected number of successes when applied to 100 cases:
Assuming stock logarithmic return follows a stable distribution, find the value at risk at the 95% level:
Compute the 95% value at risk point loss of the current S&P 500 index value, assuming the above distribution:
Find the expected shortfall of logarithmic return:
Compute the associated point loss:
A site has mean wind speed 7 m/s and Weibull distribution with shape parameter 2:
The resulting wind speed distribution over a whole year:
The power curve for a GE 1.5 MW wind turbine:
The total mean energy produced over the course of a year is then 4.3 GWh:
Estimate the distribution of the lengths of human chromosomes:
The expected chromosome length, given that the length is greater than the mean:
Properties & Relations (7)
The expectation of an expression in a continuous distribution is defined by an integral:
The expectation of an expression in a discrete distribution is defined by a sum:
Mean, Moment, Variance, and other properties are defined as expectations:
Use Expectation to find a symbolic expression for an expectation:
N[Expectation[…]] is equivalent to NExpectation if symbolic evaluation fails:
Use AsymptoticExpectation to find an asymptotic approximation of an expectation:
Compute the probability of an event:
Obtain the same result using NExpectation:
Possible Issues (1)
NExpectation may fail without a warning message in the presence of symbolic parameters:
Expectation gives a closed-form result for this example:
See Also
Expectation AsymptoticExpectation Distributed Conditioned NProbability Probability Mean Moment CentralMoment FactorialMoment NSum NIntegrate
Function Repository: KullbackLeiblerDivergence
History
Text
Wolfram Research (2010), NExpectation, Wolfram Language function, https://reference.wolfram.com/language/ref/NExpectation.html.
CMS
Wolfram Language. 2010. "NExpectation." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NExpectation.html.
APA
Wolfram Language. (2010). NExpectation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NExpectation.html
BibTeX
@misc{reference.wolfram_2025_nexpectation, author="Wolfram Research", title="{NExpectation}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/NExpectation.html}", note=[Accessed: 12-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_nexpectation, organization={Wolfram Research}, title={NExpectation}, year={2010}, url={https://reference.wolfram.com/language/ref/NExpectation.html}, note=[Accessed: 12-March-2026]}