ClosenessCentrality

ClosenessCentrality[g]

给出图 g 中顶点的紧密中心度组成的列表.

ClosenessCentrality[{vw,…}]

使用规则 vw 来指定图 g.

更多信息

  • ClosenessCentrality 对于与每个其它可到达顶点处于较短平均距离的顶点，给出较高的中心度.
  • 图的 ClosenessCentrality 由 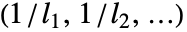给出，其中 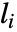是从顶点 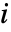到所有与 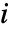连通的顶点的平均距离.
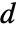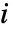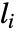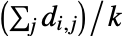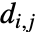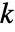  • 如果 是距离矩阵，那么从顶点 到所有连通顶点的平均距离 由 给出，其中和在所有有限 上求得，而 是与 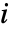相连的顶点数目.
  • 孤立顶点的紧密中心度为0.
  • ClosenessCentrality 适用于无向图、有向图、加权图、多重图和混合图.

范例

打开所有单元关闭所有单元

基本范例  (2)

计算紧密中心度：

突出显示：

对顶点排序. 排得靠前的顶点到所有其他顶点的平均距离较短：

范围  (7)

ClosenessCentrality 可用于无向图：

有向图：

加权图：

多重图：

混合图：

使用规则来指定图：

ClosenessCentrality 可用于大规模图：

应用  (9)

根据顶点到其他顶点的相对紧密程度排序：

突出显示 CycleGraph 的紧密中心度：

GridGraph:

CompleteKaryTree:

PathGraph:

计算机 ad hoc 网络可以使用 SpatialGraphDistribution 建模. 求可帮助电脑病毒在感染网络里迅速扩散的计算机：

重要计算机：

在酵母的蛋白质作用网络中，求最可能成为重要蛋白质的前10位蛋白质：

在一个基因管制网络中，如果两个基因之间有可复制的管制交互作用，则称这两个基因是连通的. 求最可能成为全局管制者的基因：

一个有向网络描述美国某中西部城市的社会福利相关的10个机构之间的信息流. 求能够与所有其他机构最有效沟通的机构：

一条公路网络连接芝加哥各个郊区. 求医院和消防队的最佳位置，以最小化急救车辆的行驶距离：

一个功率网格网络表示美国 Western States Power Grid 的拓扑图. 证明紧密中心度服从正态分布：

假定正态分布，求最大似然参数估计：

可视化比较原始分布和估计分布的概率密度函数：

对于具有 个顶点图，最中心顶点和所有其它顶点之间的紧密中心度的差值的最大和是 的倒数：

测量最中心的顶点与其他顶点的相对中心度：

社交网络中心化处理：

属性和关系  (4)

ClosenessCentrality 是到其他可到达顶点的平均距离的倒数：

到其他可达到顶点的最大距离的倒数：

紧密中心度位于0和1之间：

一个无向图的紧密中心度等同于每个分量的中心度：

对每个分量计算中心度给出相同的结果：

使用 VertexIndex 获得特定顶点的中心度：

Wolfram Research (2010)，ClosenessCentrality，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ClosenessCentrality.html （更新于 2015 年）.

文本

Wolfram Research (2010)，ClosenessCentrality，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ClosenessCentrality.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "ClosenessCentrality." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/ClosenessCentrality.html.

APA

Wolfram 语言. (2010). ClosenessCentrality. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ClosenessCentrality.html 年

BibTeX

@misc{reference.wolfram_2024_closenesscentrality, author="Wolfram Research", title="{ClosenessCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/ClosenessCentrality.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_closenesscentrality, organization={Wolfram Research}, title={ClosenessCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/ClosenessCentrality.html}, note=[Accessed: 22-November-2024 ]}