PageRankCentrality

PageRankCentrality[g,α]

gives a list of page-rank centralities for the vertices in the graph g and weight α.

PageRankCentrality[g,α,β]

gives a list of page-rank centralities, using weight α and initial centralities β.

PageRankCentrality[{vw,…},…]

uses rules vw to specify the graph g.

Details and Options

  • Page-rank centralities represent the likelihood that a person randomly following links arrives at any particular page on the web graph.
  • PageRankCentrality gives a list of centralities that are solutions to c=alpha TemplateBox[{a}, Transpose].d.c+beta, where 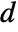is the adjacency matrix of g and 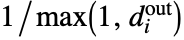is the diagonal matrix consisting of 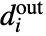, where 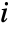is the out-degree of the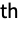 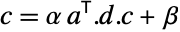^(th) vertex. »
  • If β is a scalar, it is taken to mean {β,β,…}.
  • PageRankCentrality[g,α] is equivalent to PageRankCentrality[g,α,1/VertexCount[g]].
  • Page-rank centralities are normalized.
  • The option WorkingPrecision->p can be used to control the precision used in internal computations.
  • PageRankCentrality works with undirected graphs, directed graphs, multigraphs, and mixed graphs.

Examples

open allclose all

Basic Examples  (2)

Compute page-rank centralities:

Highlight:

Find the probability that a person randomly clicking hyperlinks will arrive at a particular page:

Rank webpages, with the most visible pages first:

Scope  (7)

PageRankCentrality works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

Use rules to specify the graph:

Nondefault initial centralities:

PageRankCentrality works with large graphs:

Options  (3)

WorkingPrecision  (3)

By default, PageRankCentrality finds centralities using machine-precision computations:

Specify a higher working precision:

Infinite working precision corresponds to exact computation:

Applications  (6)

Rank websites based on the likelihood that a person randomly clicking on hyperlinks will reach a particular page:

Highlight the page-rank centrality for CycleGraph:

GridGraph:

CompleteKaryTree:

PathGraph:

A corporate network of webpages linked via hyperlinks. Find the page that you are most likely to arrive at after a large number of clicks, with a damping factor of 0.85:

A road network where a node represents a road, and two roads are connected if they intersect. Predict the road that always has a traffic flow:

Find species whose extinctions would lead to ecosystem collapse in a food chain:

A metabolic cellular network for Neisseria gonorrhoeae. Find those proteins that play a marginal functional role in the system:

These proteins have the lowest in-degree:

Properties & Relations  (3)

The centrality vector is the normalized solution of the linear system c=alpha TemplateBox[{a}, Transpose].d.c+beta:

Solve the linear system:

Page-rank centralities are normalized:

Use VertexIndex to obtain the centrality of a specific vertex:

Wolfram Research (2010), PageRankCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/PageRankCentrality.html (updated 2024).

Text

Wolfram Research (2010), PageRankCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/PageRankCentrality.html (updated 2024).

CMS

Wolfram Language. 2010. "PageRankCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/PageRankCentrality.html.

APA

Wolfram Language. (2010). PageRankCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PageRankCentrality.html

BibTeX

@misc{reference.wolfram_2024_pagerankcentrality, author="Wolfram Research", title="{PageRankCentrality}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/PageRankCentrality.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pagerankcentrality, organization={Wolfram Research}, title={PageRankCentrality}, year={2024}, url={https://reference.wolfram.com/language/ref/PageRankCentrality.html}, note=[Accessed: 22-December-2024 ]}