CombinatorC
✖
CombinatorC
[Experimental]
![TemplateBox[{}, CombinatorC]](Files/CombinatorC.en/1.png "TemplateBox[{}, CombinatorC]"){kind=small}
Details
- The
![TemplateBox[{}, CombinatorC]](Files/CombinatorC.en/2.png "TemplateBox[{}, CombinatorC]")
combinator has the property that ![TemplateBox[{}, CombinatorC]xyz](Files/CombinatorC.en/3.png "TemplateBox[{}, CombinatorC]xyz")
reduces to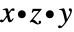 
. - No transformations for CombinatorC are applied automatically.
- CombinatorC is output in StandardForm or TraditionalForm as
![TemplateBox[{}, CombinatorC]](Files/CombinatorC.en/5.png "TemplateBox[{}, CombinatorC]")
. This typeset form can be input using 
cC
.
Examples
open allclose allBasic Examples (1)Summary of the most common use cases
![TemplateBox[{}, CombinatorC]](Files/CombinatorC.en/12.png "TemplateBox[{}, CombinatorC]"){kind=small}
![TemplateBox[{}, CombinatorS]](Files/CombinatorC.en/13.png "TemplateBox[{}, CombinatorS]"){kind=small}
![TemplateBox[{}, CombinatorK]](Files/CombinatorC.en/14.png "TemplateBox[{}, CombinatorK]"){kind=small}
(TemplateBox[{}, CombinatorS](TemplateBox[{}, CombinatorK]TemplateBox[{}, CombinatorK])TemplateBox[{}, CombinatorS]))(TemplateBox[{}, CombinatorK]TemplateBox[{}, CombinatorK])](Files/CombinatorC.en/15.png "TemplateBox[{}, CombinatorS](TemplateBox[{}, CombinatorS](TemplateBox[{}, CombinatorK]TemplateBox[{}, CombinatorS])(TemplateBox[{}, CombinatorS](TemplateBox[{}, CombinatorK]TemplateBox[{}, CombinatorK])TemplateBox[{}, CombinatorS]))(TemplateBox[{}, CombinatorK]TemplateBox[{}, CombinatorK])"){kind=small}
Wolfram Research (2020), CombinatorC, Wolfram Language function, https://reference.wolfram.com/language/ref/CombinatorC.html.
✖
Wolfram Research (2020), CombinatorC, Wolfram Language function, https://reference.wolfram.com/language/ref/CombinatorC.html.Text
Wolfram Research (2020), CombinatorC, Wolfram Language function, https://reference.wolfram.com/language/ref/CombinatorC.html.
✖
Wolfram Research (2020), CombinatorC, Wolfram Language function, https://reference.wolfram.com/language/ref/CombinatorC.html.CMS
Wolfram Language. 2020. "CombinatorC." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CombinatorC.html.
✖
Wolfram Language. 2020. "CombinatorC." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CombinatorC.html.APA
Wolfram Language. (2020). CombinatorC. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CombinatorC.html
✖
Wolfram Language. (2020). CombinatorC. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CombinatorC.htmlBibTeX
✖
@misc{reference.wolfram_2025_combinatorc, author="Wolfram Research", title="{CombinatorC}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CombinatorC.html}", note=[Accessed: 27-March-2025
]}BibLaTeX
✖
@online{reference.wolfram_2025_combinatorc, organization={Wolfram Research}, title={CombinatorC}, year={2020}, url={https://reference.wolfram.com/language/ref/CombinatorC.html}, note=[Accessed: 27-March-2025
]}