ConjugateTranspose
or ![]() gives the conjugate transpose of
gives the conjugate transpose of ![]() .
.
Details and Options
- ConjugateTranspose[m] is equivalent to Conjugate[Transpose[m]]. »
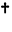 can be entered as
can be entered as  ct
ct or \[ConjugateTranspose].
or \[ConjugateTranspose].- ConjugateTranspose[m] can also be given as
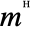 , where
, where 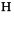 can be entered as
can be entered as  hc
hc or \[HermitianConjugate].
or \[HermitianConjugate]. - ConjugateTranspose[m,spec] gives Conjugate[Transpose[m,spec]].
Examples
open allclose allScope (12)
Matrices (7)
Conjugate-transpose the matrix and format the result:
Conjugate and transpose a row matrix into a column matrix:
Conjugate and transpose the column matrix back into a row matrix:
ConjugateTranspose[vec] conjugates the entries but does not change the shape of vec:
ConjugateTranspose works for symbolic matrices:
Use ComplexExpand to assume all variables are real:
ConjugateTranspose leaves the identity matrix unchanged:
The conjugate transpose is also sparse:
Transpose a SymmetrizedArray object:
As the matrix is antihermitian, the result is the negation of the original:
Format a symbolic conjugate transpose in TraditionalForm:
Arrays (5)
Conjugate-transpose the first two levels of a rank-3 array, effectively treating it as a matrix of vectors:
Transpose an array of depth 3 using different permutations:
Perform transpositions using TwoWayRule notation:
Transpose levels 2 and 3 of a depth-4 array:
The second and third dimensions have been exchanged:
Get the conjugated leading diagonal by transposing two identical levels:
Applications (10)
Matrix Decompositions (4)
Find the QRDecomposition of ![]() :
:
![]() is unitary, so its inverse is
is unitary, so its inverse is ![]() :
:
Reconstruct ![]() from the decomposition:
from the decomposition:
Compute the SchurDecomposition of a matrix ![]() :
:
The matrix ![]() is unitary, so its inverse is
is unitary, so its inverse is ![]() :
:
Reconstruct ![]() from the decomposition:
from the decomposition:
Compute the SingularValueDecomposition of a matrix ![]() :
:
The matrices ![]() and
and ![]() are unitary, so their inverses are their conjugate transposes:
are unitary, so their inverses are their conjugate transposes:
Reconstruct ![]() from the decomposition:
from the decomposition:
Construct the singular value decomposition of ![]() , a random
, a random ![]() complex matrix:
complex matrix:
First compute the eigensystem of ![]() :
:
The singular values are the square roots of the nonzero eigenvalues:
The ![]() matrix is a diagonal matrix of singular values with the same shape as
matrix is a diagonal matrix of singular values with the same shape as ![]() :
:
The ![]() matrix has the eigenvectors as its columns:
matrix has the eigenvectors as its columns:
The ![]() matrix has columns of the form
matrix has columns of the form ![]() for each of the nonzero eigenvalues:
for each of the nonzero eigenvalues:
Special Matrices (6)
A Hermitian matrix obeys ![]() , an antihermitian matrix
, an antihermitian matrix ![]() . This matrix is Hermitian:
. This matrix is Hermitian:
Confirm with HermitianMatrixQ:
Confirm with AntihermitianMatrixQ:
A matrix is unitary if ![]() . Check if the matrix
. Check if the matrix ![]() is unitary:
is unitary:
Confirm that it is unitary using UnitaryMatrixQ:
A Hermitian matrix is unitarily diagonalizable as ![]() , with
, with ![]() diagonal and real valued and
diagonal and real valued and ![]() unitary. Verify that the following matrix is Hermitian and then diagonalize it:
unitary. Verify that the following matrix is Hermitian and then diagonalize it:
To diagonalize, first compute ![]() 's eigenvalues and place them in a diagonal matrix:
's eigenvalues and place them in a diagonal matrix:
Next, compute the unit eigenvectors:
Then ![]() can be diagonalized with
can be diagonalized with ![]() as previously, and
as previously, and ![]() :
:
An antihermitian matrix is unitarily diagonalizable as ![]() , with
, with ![]() diagonal and imaginary valued and
diagonal and imaginary valued and ![]() unitary. Verify that the following matrix is antihermitian and then diagonalize it:
unitary. Verify that the following matrix is antihermitian and then diagonalize it:
To diagonalize, first compute ![]() 's eigenvalues and place them in a diagonal matrix:
's eigenvalues and place them in a diagonal matrix:
Next, compute the unit eigenvectors:
Then ![]() can be diagonalized with
can be diagonalized with ![]() as previously, and
as previously, and ![]() :
:
An unitary matrix is itself unitarily diagonalizable as ![]() , with
, with ![]() unitary and
unitary and ![]() diagonal with entries that lie on the unit circle. Verify that the following matrix is unitary and then diagonalize it:
diagonal with entries that lie on the unit circle. Verify that the following matrix is unitary and then diagonalize it:
The eigenvalues all lie on the unit circle:
Place the eigenvalues in a diagonal matrix:
Normalize the eigenvectors and place them in a column matrix:
A matrix ![]() is called normal if
is called normal if ![]() . Normal matrices are the most general kind of matrix that can be unitarily diagonalized as
. Normal matrices are the most general kind of matrix that can be unitarily diagonalized as ![]() with
with ![]() diagonal and
diagonal and ![]() unitary. All Hermitian matrices
unitary. All Hermitian matrices ![]() are normal because both sides of the equality are simply
are normal because both sides of the equality are simply ![]() :
:
Similarly, all antihermitian matrices are normal because both sides of the equality are simply ![]() :
:
Unitary matrices are normal, as substituting in the definition ![]() gives an identity matrix on both sides:
gives an identity matrix on both sides:
Show that the following matrix is normal, then diagonalize it:
Confirm using NormalMatrixQ:
A normal matrix like ![]() can be unitarily diagonalized using Eigensystem:
can be unitarily diagonalized using Eigensystem:
The entries on the diagonal can be arbitrary complex numbers:
Normalizing the eigenvectors and putting them in columns gives a unitary matrix:
Properties & Relations (10)
ConjugateTranspose[m] is equivalent to Conjugate[Transpose[m]]:
ConjugateTranspose obeys ![]() :
:
For compatible matrices ![]() and
and ![]() , ConjugateTranspose obeys
, ConjugateTranspose obeys ![]() :
:
Matrix inversion commutes with ConjugateTranspose, i.e. ![]() :
:
Many special matrices are defined by their properties under ConjugateTranspose. A Hermitian matrix has ![]() :
:
The product of a matrix and its conjugate transpose is Hermitian:
![]() is the matrix product of
is the matrix product of ![]() and
and ![]() :
:
The sum of a square matrix and its conjugate transpose is Hermitian:
The difference is antihermitian:
Transposition of {{}} returns {}:
The result cannot be {{}} again because the permutation of the dimensions {1,0} is {0,1} and no expression can have dimensions {0,1}:
ConjugateTranspose[a] transposes the first two levels of an array:
ConjugateTranspose[a,perm] returns an array of dimensions Permute[Dimensions[a],perm]:
Text
Wolfram Research (2004), ConjugateTranspose, Wolfram Language function, https://reference.wolfram.com/language/ref/ConjugateTranspose.html.
CMS
Wolfram Language. 2004. "ConjugateTranspose." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ConjugateTranspose.html.
APA
Wolfram Language. (2004). ConjugateTranspose. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConjugateTranspose.html