ConoverTest

ConoverTest[{data1,data2,…}]

data1, data2, …の分散が等しいかどうかの検定を行う．

ConoverTest[dspec,]

に対する分散尺度の検定を行う．

ConoverTest[dspec,,"property"]

"property"の値を返す．

詳細とオプション

  • ConoverTestは，帰無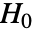仮説 と対立仮説 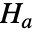で検定を行う．
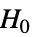
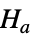
  • {data1,data2}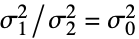
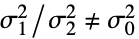
    {data1,data2,…}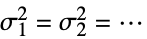すべてが等しいわけではない
  • ただし，σi2は dataiの母分散である．
  • デフォルトで，確率値すなわち 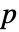値が返される．
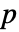  • 値が小さければ 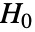が真である可能性は低い．
  • dspec 中の data は一変量{x1,x2,…}でなければならない．
  • 引数 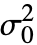は任意の正の実数でよい．特に指定されていない限り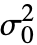のデフォルト値は1であり，dspec 内のグループ数が2よりも多い場合は無視される．
  • ConoverTestは data が共通の中央値について対称であると仮定する．
  • ConoverTest[data,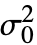,"HypothesisTestData"]は htd["property"]の形で追加的な検定結果と特性の抽出に利用できるHypothesisTestDataオブジェクト htd を返す．
  • ConoverTest[data,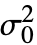,"property"]を使って直接"property"の値を与えることができる．
  • 検定結果のレポートに関連する特性
  • "PValue" 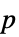値のリスト
    "PValueTable" 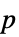値のフォーマットされた表
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 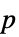値のペアのリスト
    "TestDataTable" 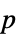値と検定統計のフォーマットされた表
    "TestStatistic"検定統計のリスト
    "TestStatisticTable"検定統計のフォーマットされた表
  • 検定統計はサンプル中央値からの絶対偏差の順位の平方に基づく．
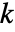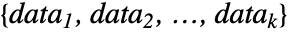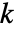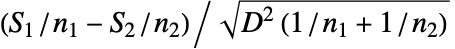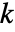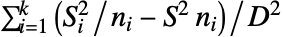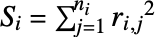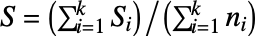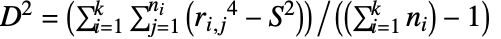  • サンプル数が 個，つまり datai={xi,1,xi,2,…,xi,ni}での場合，値 xi,jの順位 ri,jはすべての要素 {zi,j}1≤i≤k,1≤j≤ni中の zi,jの順位である．ただし，zi,j=Abs[xi,j-Median[datai]]．検定統計は， が2の場合はで， が2より大きい場合はで与えられる．ただし，, かつ である．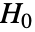
  • の下で，ConoverTestの検定統計は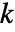， が2のときはNormalDistribution[0,1]に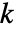， が2より大きいときはChiSquareDistribution[k-1]に従うと仮定される．
  • ConoverTestは二乗順位検定と呼ばれることもあり，dataiが正規分布に従っていない場合にはFisherRatioTestの代りとなる．
  • 使用可能なオプション
  • AlternativeHypothesis "Unequal"対立仮説のための不等式
    SignificanceLevel 0.05診断とレポートのための切捨て
    VerifyTestAssumptions Automaticどの診断検定を実行するのかを設定する
  • ConoverTestでは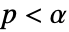， のときにのみ 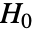が棄却されるような切捨て 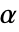が選ばれる．"TestConclusion"および"ShortTestConclusion"特性に使われる 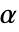の値はSignificanceLevelオプションで制御される．値 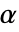は対称性の検定を含む仮定の診断検定にも使われる．デフォルトで 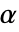は0.05に設定される．
  • ConoverTestにおけるVerifyTestAssumptionsの名前付き設定
  • "Symmetry"すべてのデータが対称であることを検証する

例題

すべて開くすべて閉じる

例  (2)

2つのデータ集合の分散を等価性について調べる：

さらに特性を抽出するためにHypothesisTestDataオブジェクトを作る：

調べる特性：

2つの母分散比を特定の値について検定する：

対立仮説 で検定を行う：

スコープ  (8)

検定  (6)

2つの母分散を比べる：

の下， 値は[0,1]で一様に分布している：

Conover検定の 値のサンプルのヒストグラム：

が偽のときは， 値は小さいことが多い：

2つの母分散比が特定の値であるかどうかを検定する：

以下の形式は等しい：

を決定する場合には，データ集合の順序を考慮すべきである：

3つの母集団の分散が同一であるかどうかの検定を行う：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出に使える特性：

HypothesisTestDataオブジェクトから特性をいくつか抽出する：

値と検定統計：

任意数の特性を同時に抽出する：

値と検定統計：

レポート  (2)

検定結果を表にする：

表の値は，"TestData"を使って抽出できる：

値あるいは検定統計を表にする：

表からの 値：

表からの検定統計：

オプション  (6)

AlternativeHypothesis  (3)

デフォルトで両側検定が行われる：

両側検定を行う．あるいは2つの片側検定のうちの1つを代りに行う：

対 を検定する：

対 を検定する：

対 を検定する：

ヌル値が与えられている場合に，片側検定を代りに行う：

対 を検定する：

対 を検定する：

SignificanceLevel  (1)

有意水準は"TestConclusion"と"ShortTestConclusion"に使われる：

VerifyTestAssumptions  (2)

診断は，AllあるいはNoneを使ってまとめて制御することができる：

すべての仮定を検証する：

どの仮定もチェックしない：

診断は個々に制御することができる：

対称性をチェックする：

対称性の仮定をTrueに設定する：

アプリケーション  (1)

1990年代の前半と後半において，S&P 500の日々の点の変化の分散を比べる：

データは明らかに正規分布に従っていない：

1990年代前半における変動量は，後半よりもかなり低い：

特性と関係  (8)

グループ数が2のとき，検定統計は の下でNormalDistribution[0,1]に従う：

グループ数が ()のとき，検定統計は の下でChiSquareDistribution[k-1]に従う：

FisherRatioTestと違って，Conover検定は正規性を仮定しない：

FisherRatioTestの結果は， 値を過小評価する：

Conover検定は，データが共通の中央値について対称であると仮定する：

検定統計の分布は，データが非対称である場合，標準正規分布に従わない：

ConoverTestの検定統計は順位に基づく：

同順位のものがなければ，Orderingを使って順位を計算することができる：

検定統計：

PearsonChiSquareTestを使って，共通の中央値においてデータの対称性を検定する：

データは対称であり，警告メッセージは出されない：

警告メッセージの 値は，PearsonChiSquareTestのそれに一致する：

Conover検定は，入力がTimeSeriesのときはタイムスタンプを無視する：

Conover検定はTemporalDataの経路構造を認識する：

値を直接使う：

考えられる問題  (3)

データは，共通の中央値において対称でなければならない：

位置のシフトを考慮に入れると，最初の2つのデータ集合は対称である：

最後2つのデータ集合は，共通の中央値において対称ではない：

グループ数が2より多いとき，Conover検定は引数 を無視する：

データ内に2より多いグループがある場合，Conover検定は対立仮説として両側検定しか認めない：

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

特定の対立仮説によって与えられた検定統計：

検定統計の分布を比較する：

Wolfram Research (2010), ConoverTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/ConoverTest.html （2017年に更新）.

テキスト

Wolfram Research (2010), ConoverTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/ConoverTest.html （2017年に更新）.

CMS

Wolfram Language. 2010. "ConoverTest." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/ConoverTest.html.

APA

Wolfram Language. (2010). ConoverTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConoverTest.html

BibTeX

@misc{reference.wolfram_2025_conovertest, author="Wolfram Research", title="{ConoverTest}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/ConoverTest.html}", note=[Accessed: 05-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_conovertest, organization={Wolfram Research}, title={ConoverTest}, year={2017}, url={https://reference.wolfram.com/language/ref/ConoverTest.html}, note=[Accessed: 05-July-2025 ]}