represents a ![]() distribution with ν degrees of freedom.
distribution with ν degrees of freedom.


ChiSquareDistribution
represents a ![]() distribution with ν degrees of freedom.
distribution with ν degrees of freedom.
Details
- The probability density for value
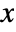 in a
in a 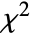 distribution is proportional to
distribution is proportional to 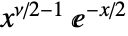 for
for 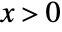 , and is zero for
, and is zero for 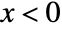 . »
. » - For integer ν, the
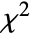 distribution with ν degrees of freedom gives the distribution of sums of squares of ν values independently sampled from a normal distribution.
distribution with ν degrees of freedom gives the distribution of sums of squares of ν values independently sampled from a normal distribution. - ChiSquareDistribution allows ν to be any positive real number.
- ChiSquareDistribution allows ν to be a dimensionless quantity. »
- ChiSquareDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- ChiSquareDistribution[ν] represents a statistical distribution parametrized by a positive value ν indicating the degrees of freedom of the distribution. ν determines the general shape of the probability density function (PDF) of a chi-square distribution, and, depending on the values of ν, the PDF may be either monotonic decreasing or may have a single "peak" (i.e. a global maximum) with a potential singularity approaching the lower boundary of its domain.
- ChiSquareDistribution is the distribution followed by the square of a chi-distributed random variable. In other words, if
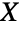 is a random variable and
is a random variable and 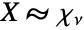 (where
(where 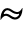 denotes "is distributed as"), then
denotes "is distributed as"), then 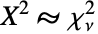 . The sum
. The sum 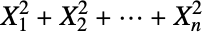 of a collection
of a collection 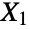 ,
, 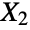 , …,
, …, 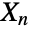 of identically normally distributed independent random variables is also chi-square distributed. The chi-square distribution can be used to quantify the goodness of fit between a theoretical or empirical model and a collection of samples. Specific applications include magnetic resonance imaging and the analysis of possible associations between disease exposure and transmission.
of identically normally distributed independent random variables is also chi-square distributed. The chi-square distribution can be used to quantify the goodness of fit between a theoretical or empirical model and a collection of samples. Specific applications include magnetic resonance imaging and the analysis of possible associations between disease exposure and transmission. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a chi-square distribution. Distributed[x,ChiSquareDistribution[ν]], written more concisely as xChiSquareDistribution[ν], can be used to assert that a random variable x is distributed according to a chi-square distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for chi-square distributions may be given using PDF[ChiSquareDistribution[ν],x] and CDF[ChiSquareDistribution[ν],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a chi-square distribution, EstimatedDistribution to estimate a chi-square parametric distribution from given data, and FindDistributionParameters to fit data to a chi-square distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic chi-square distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic chi-square distribution.
- TransformedDistribution can be used to represent a transformed chi-square distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a chi-square distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving chi-square distributions.
- ChiSquareDistribution is closely related to a number of other distributions. For example, several distributions, including GammaDistribution, ExponentialDistribution, InverseChiSquareDistribution, UniformDistribution, and LaplaceDistribution, can be obtained by transformations of ChiSquareDistribution, while NormalDistribution and FRatioDistribution are limiting values for transformed versions of ChiSquareDistribution. Moreover, ChiSquareDistribution can be viewed as a special case of a number of other more general distributions, including RayleighDistribution, MaxwellDistribution, PearsonDistribution, and ParetoDistribution. ChiSquareDistribution is also closely related to BetaDistribution, StudentTDistribution, UniformDistribution, and NoncentralChiSquareDistribution.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a ![]() distribution:
distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare density histogram of the sample with the PDF of the estimated distribution:
For a large number of degrees of freedom, the distribution becomes symmetric:
The limiting value is the kurtosis of NormalDistribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Cumulant has closed form:
Use dimensionless Quantity to specify the degree of freedom parameter ν:
Applications (2)
ChiSquareDistribution is used in exact (small) sampling theory. Define ![]() statistics:
statistics:
If data comes from a NormalDistribution, then ![]() statistics follow ChiSquareDistribution, even for data that is a sample of small size (less than 30):
statistics follow ChiSquareDistribution, even for data that is a sample of small size (less than 30):
The weight in grams of a particular boxed cereal product is known to follow a normal distribution. A quality assurance team samples 15 boxes at random and records their weights. Test the hypothesis that the standard deviation of the product weight is less than 36:
Under the null hypothesis of ![]() , the following statistic follows ChiSquareDistribution:
, the following statistic follows ChiSquareDistribution:
The null hypothesis cannot be rejected at the 5% level:
Assuming that the standard deviation of the product weight equals 32, compute the probability of rejecting the null hypothesis, also known as the power of the test, at the 5% level as a function of sample size:
Find the sample size required for the power of the test to be at least 80%:
Properties & Relations (23)
ChiSquareDistribution[ν] converges to a normal distribution as ν->∞:
Sum of ![]() -distributed variables follows
-distributed variables follows ![]() distribution:
distribution:
Relationships to other distributions:
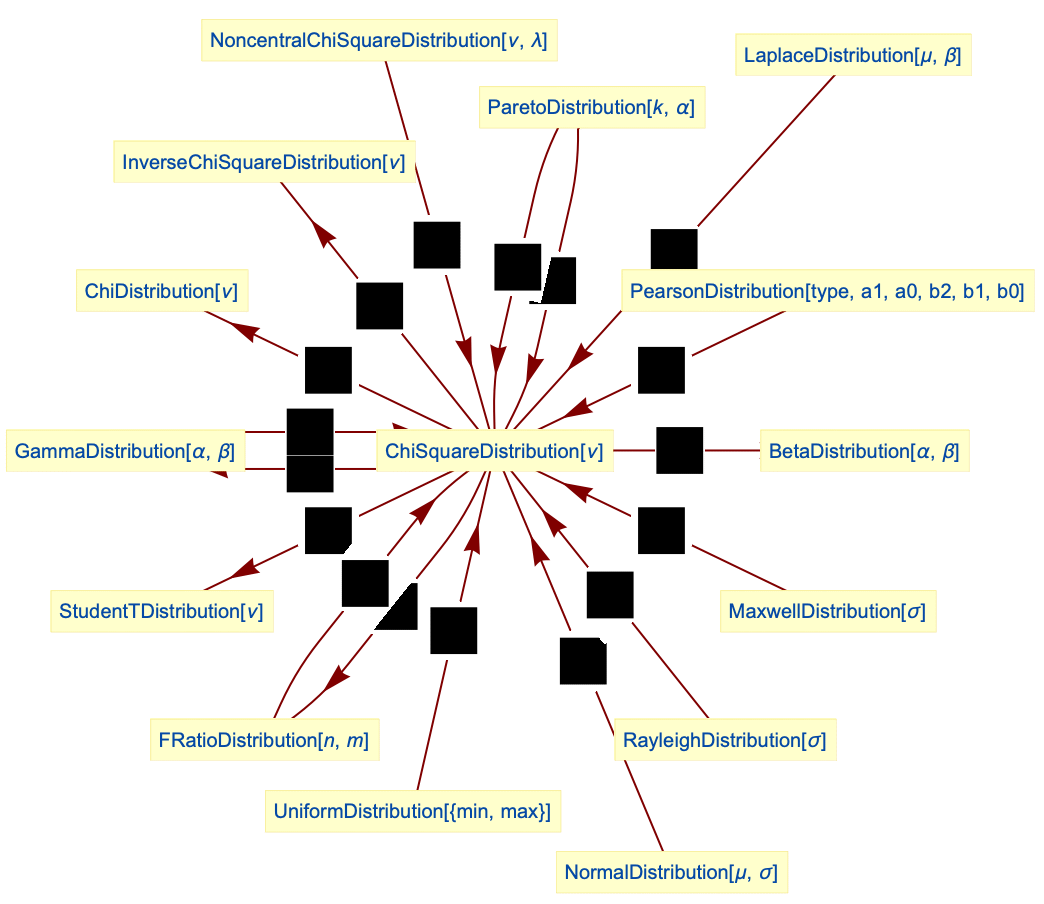
NoncentralChiSquareDistribution simplifies to ![]() distribution:
distribution:
![]() distribution is a limiting case of FRatioDistribution:
distribution is a limiting case of FRatioDistribution:
The ratio of two ![]() -distributed variables follows FRatioDistribution:
-distributed variables follows FRatioDistribution:
Sum of squares of ![]() variables from NormalDistribution follows
variables from NormalDistribution follows ![]() distribution:
distribution:
![]() distribution is a special case of GammaDistribution:
distribution is a special case of GammaDistribution:
Scaled ![]() distribution follows GammaDistribution:
distribution follows GammaDistribution:
The square root of a ![]() variable follows the ChiDistribution:
variable follows the ChiDistribution:
Square of RayleighDistribution with ![]() is a special case of
is a special case of ![]() distribution:
distribution:
Square of MaxwellDistribution with ![]() is a special case of
is a special case of ![]() distribution:
distribution:
![]() distribution and InverseChiSquareDistribution have an inverse relationship:
distribution and InverseChiSquareDistribution have an inverse relationship:
![]() distribution is a special case of type 3 PearsonDistribution:
distribution is a special case of type 3 PearsonDistribution:
A transformation of ![]() distribution yields BetaDistribution:
distribution yields BetaDistribution:
![]() is a transformation of UniformDistribution:
is a transformation of UniformDistribution:
![]() distribution is a transformation of LaplaceDistribution:
distribution is a transformation of LaplaceDistribution:
![]() distribution is a transformation of ParetoDistribution:
distribution is a transformation of ParetoDistribution:
![]() distribution is a transformation of ParetoDistribution:
distribution is a transformation of ParetoDistribution:
StudentTDistribution is a transformation of ![]() distribution:
distribution:
StudentTDistribution can be obtained from ChiSquareDistribution and NormalDistribution:
NoncentralBetaDistribution can be obtained as a transformation of ChiSquareDistribution and NoncentralChiSquareDistribution:
NoncentralStudentTDistribution can be obtained from NormalDistribution and ChiSquareDistribution:
Possible Issues (2)
ChiSquareDistribution is not defined when ν is not a positive real number:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
See Also
StudentTDistribution FRatioDistribution GammaDistribution ChiDistribution NoncentralChiSquareDistribution InverseChiSquareDistribution FindFit
Function Repository: ChiSquareCI
Tech Notes
Text
Wolfram Research (2007), ChiSquareDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ChiSquareDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "ChiSquareDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ChiSquareDistribution.html.
APA
Wolfram Language. (2007). ChiSquareDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ChiSquareDistribution.html
BibTeX
@misc{reference.wolfram_2025_chisquaredistribution, author="Wolfram Research", title="{ChiSquareDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ChiSquareDistribution.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_chisquaredistribution, organization={Wolfram Research}, title={ChiSquareDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ChiSquareDistribution.html}, note=[Accessed: 17-January-2026]}