LocationEquivalenceTest[{data1,data2,…}]
tests whether the means or medians of the datai are equal.
LocationEquivalenceTest[{data1,…},"property"]
returns the value of "property".


LocationEquivalenceTest
LocationEquivalenceTest[{data1,data2,…}]
tests whether the means or medians of the datai are equal.
LocationEquivalenceTest[{data1,…},"property"]
returns the value of "property".
Details and Options




- LocationEquivalenceTest performs a hypothesis test on the datai with null hypothesis
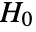 that the true location parameters of the populations are equal,
that the true location parameters of the populations are equal, 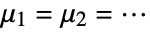 , and alternative hypothesis
, and alternative hypothesis 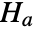 that at least one is different.
that at least one is different. - By default, a probability value or
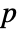 -value is returned.
-value is returned. - A small
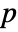 -value suggests that it is unlikely that
-value suggests that it is unlikely that 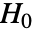 is true.
is true. - The datai must be univariate {x1,x2,…}.
- LocationEquivalenceTest[{data1,…}] will choose the most powerful test that applies to the data.
- LocationEquivalenceTest[{data1,…},All] will choose all tests that apply to the data.
- LocationEquivalenceTest[{data1,…},"test"] reports the
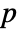 -value according to "test".
-value according to "test". - Mean-based tests assume that the datai are normally distributed. The median-based Kruskal–Wallis test assumes that datai are symmetric about a common median. The complete block
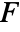 and Friedman rank tests assume that the data is in randomized complete blocks. All of the tests require the datai to have equal variances.
and Friedman rank tests assume that the data is in randomized complete blocks. All of the tests require the datai to have equal variances. - The following tests can be used:
-
"CompleteBlockF" normality, blocked mean test for complete block design "FriedmanRank" blocked median test for complete block design "KruskalWallis" symmetry median test for two or more samples "KSampleT" normality mean test for two or more samples - The complete block
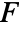 test effectively performs one-way analysis of variance for randomized complete block design.
test effectively performs one-way analysis of variance for randomized complete block design. - The Friedman rank test ranks observations across rows and sums the ranks along columns in the data to arrive at the test statistic. The statistic is corrected for ties.
- The Kruskal–Wallis test effectively performs a one-way analysis of variance on the ranks of the data. The test statistic is corrected for ties.
- The
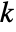 -sample
-sample 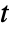 -test is equivalent to a one-way analysis of variance of the data.
-test is equivalent to a one-way analysis of variance of the data. - LocationEquivalenceTest[{data1,…},"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
- LocationEquivalenceTest[{data1,…},"property"] can be used to directly give the value of "property".
- Properties related to the reporting of test results include:
-
"AllTests" list of all applicable tests "AutomaticTest" test chosen if Automatic is used "DegreesOfFreedom" the degrees of freedom used in a test "PValue" list of 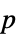 -values
-values"PValueTable" formatted table of 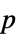 -values
-values"ShortTestConclusion" a short description of the conclusion of a test "TestConclusion" a description of the conclusion of a test "TestData" list of pairs of test statistics and 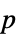 -values
-values"TestDataTable" formatted table of 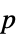 -values and test statistics
-values and test statistics"TestStatistic" list of test statistics "TestStatisticTable" formatted table of test statistics - The following options can be given:
-
Method Automatic the method to use for computing 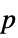 -values
-valuesSignificanceLevel 0.05 cutoff for diagnostics and reporting VerifyTestAssumptions Automatic what assumptions to verify - For tests of location, a cutoff
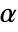 is chosen such that
is chosen such that 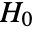 is rejected only if
is rejected only if 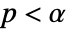 . The value of
. The value of 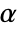 used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value
used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value 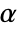 is also used in diagnostic tests of assumptions, including tests for normality, equal variance, and symmetry. By default,
is also used in diagnostic tests of assumptions, including tests for normality, equal variance, and symmetry. By default, 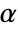 is set to 0.05.
is set to 0.05. - Named settings for VerifyTestAssumptions in LocationEquivalenceTest include:
-
"Normality" verify that all data is normally distributed "EqualVariance" verify that the datai have equal variances "Symmetry" verify symmetry about a common median
Examples
open all close allBasic Examples (3)
Test whether the means or medians from two or more populations are all equivalent:
Create a HypothesisTestData object for repeated property extraction:
The complete block ![]() test can be used to test for mean differences with complete block design:
test can be used to test for mean differences with complete block design:
There is a significant difference among the means at the 0.05 level:
Use the Friedman rank test to test for differences in medians with complete block design:
It appears that at least one median differs significantly from the others:
Scope (9)
Testing (5)
Perform a particular test for equal locations:
Any number of tests can be performed simultaneously:
Perform all tests appropriate to the data simultaneously:
Use the property "AllTests" to identify which tests were used:
Create a HypothesisTestData object for repeated property extraction:
The properties available for extraction:
Extract some properties from a HypothesisTestData object:
The ![]() -value and test statistic from a
-value and test statistic from a ![]() -sample
-sample ![]() -test:
-test:
Reporting (4)
Tabulate the results from a selection of tests:
A full table of all appropriate test results:
A table of selected test results:
Retrieve the entries from a test table for customized reporting:
The ![]() -values are above 0.05, so there is not enough evidence to reject
-values are above 0.05, so there is not enough evidence to reject ![]() at that level:
at that level:
Tabulate ![]() -values for a test or group of tests:
-values for a test or group of tests:
A table of ![]() -values from all appropriate tests:
-values from all appropriate tests:
A table of ![]() -values from a subset of tests:
-values from a subset of tests:
Report the test statistic from a test or group of tests:
Options (8)
Method (2)
Compute the Kruskal–Wallis test for a group of datasets:
The rescaled test statistic follows an FRatioDistribution:
Use the asymptotic chi-square approximation:
Use the asymptotic chi-square distribution for the Friedman rank test:
SignificanceLevel (3)
VerifyTestAssumptions (3)
Applications (4)
Test whether a group of populations shares a common location:
The first group of datasets was drawn from populations with very different locations:
Populations represented by the second group all have similar locations:
Morphological measures of two crab varieties were taken for each of the two sexes. Determine whether the measures differ across the various groups:
The rear width is the only measure that differs by gender when variety is ignored:
All measures are significantly different when gender and variety are considered simultaneously:
A pilot study was conducted for 75 patients with type II diabetes who had failed to achieve target weight loss with a particular medication. The patients were randomly assigned to three groups: a control group continuing the original medication, and two treatment groups that received 50 and 100 mg of a new medication, respectively. Weight loss in pounds over a 12-week period was recorded:
There is a significant difference in the means of the groups:
Using a Bonferroni correction in a test of each pairwise difference shows that both treatment levels perform better than the control, but that they are not significantly different from one another:
A group of six food critics rated four restaurants for quality on a 100-point scale. Determine whether there is a significant difference in the quality of the restaurants according to critics:
Bar charts of the median score by critic:
Bar charts of the median score for each restaurant:
Accounting for the blocked structure, a significant difference in quality can be detected:
Properties & Relations (12)
The ![]() -value returned by a
-value returned by a ![]() -sample
-sample ![]() -test is equivalent to that of TTest for two samples:
-test is equivalent to that of TTest for two samples:
The Kruskal–Wallis test is a ![]() -sample extension of the two-sample Mann–Whitney test:
-sample extension of the two-sample Mann–Whitney test:
The Mann–Whitney ![]() -value is corrected for continuity and ties:
-value is corrected for continuity and ties:
Under ![]() the
the ![]() -sample
-sample ![]() -test statistic follows an FRatioDistribution[g-1,n-g], where g is the number of datasets and n is the total number of observations:
-test statistic follows an FRatioDistribution[g-1,n-g], where g is the number of datasets and n is the total number of observations:
Under ![]() the complete block
the complete block ![]() and Friedman rank test statistics with t treatments and g blocks follows an FRatioDistribution[t-1,(g-1)(t-1)]:
and Friedman rank test statistics with t treatments and g blocks follows an FRatioDistribution[t-1,(g-1)(t-1)]:
The Friedman statistic can be transformed to follow a ChiSquareDistribution[g-1]:
Compute a ![]() -value using ChiSquareDistribution:
-value using ChiSquareDistribution:
This transformation is done automatically with Method set to "Asymptotic":
Under ![]() the Kruskal–Wallis test statistic asymptotically follows a ChiSquareDistribution[g-1] where g is the number of datasets:
the Kruskal–Wallis test statistic asymptotically follows a ChiSquareDistribution[g-1] where g is the number of datasets:
By default, the test statistic is rescaled to follow an FRatioDistribution[g-1,n-g]:
Conceptually, a comparison is made between the pooled and average individual variances:
Larger pooled variances indicate different means:
The ratio of pooled to individual variances:
LocationEquivalenceTest effectively detects how far this ratio is from 1:
The ![]() and
and ![]() test statistics are used in LocationEquivalenceTest:
test statistics are used in LocationEquivalenceTest:
The Kruskal–Wallis statistic is rank-based:
For ![]() -sample
-sample ![]() and Kruskal–Wallis tests, the statistic can be computed using LinearModelFit:
and Kruskal–Wallis tests, the statistic can be computed using LinearModelFit:
The Kruskal–Wallis test is identical but uses ranks:
Use LocationTest for two datasets:
LocationTest can also test more complicated hypotheses:
The location equivalence test ignores the time stamps when the input is a TimeSeries:
The location equivalence test recognizes the path structure of a TemporalData:
Possible Issues (3)
All of the tests require that the data has equal variances:
The ![]() -sample
-sample ![]() -test and complete block
-test and complete block ![]() test require that the data is normally distributed:
test require that the data is normally distributed:
The Kruskal–Wallis test or Friedman rank test should be used if the data is not normally distributed:
The Friedman rank and complete block ![]() tests require equal sample sizes:
tests require equal sample sizes:
Related Guides
History
Text
Wolfram Research (2010), LocationEquivalenceTest, Wolfram Language function, https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html.
CMS
Wolfram Language. 2010. "LocationEquivalenceTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html.
APA
Wolfram Language. (2010). LocationEquivalenceTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html
BibTeX
@misc{reference.wolfram_2025_locationequivalencetest, author="Wolfram Research", title="{LocationEquivalenceTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_locationequivalencetest, organization={Wolfram Research}, title={LocationEquivalenceTest}, year={2010}, url={https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html}, note=[Accessed: 08-January-2026]}