CoordinateChartData

CoordinateChartData[chart,property]

chart の指定された特性の値を与える．

CoordinateChartData[chart,property,{x1,x2,…,xn}]

chart の指定された特性の，点{x1,x2,…,xn}で評価された値を与える．

詳細

  • 座標チャートは座標系の名前，ペア{coordsys,dim}，あるいは{coordsys,metric,dim}という形の標準名で指定することができる．次元 dim は正の整数である．ペア{coordsys,dim}はユークリッド計量に言及しているものと解釈される．
  • 有効な計量指定
  • "metric"デフォルトのパラメータ値がある計量
    {"metric",param}1つのパラメータが指定された計量
    {"metric",{param1,param2,…}}複数のパラメータが指定された計量
  • 有効な座標系指定
  • "coordsys"デフォルトのパラメータ値のある座標系
    {"coordsys",param}1つのパラメータが指定された座標系
    {"coordsys",{param1,param2,…}}複数のパラメータが指定された座標系
  • 評価点{x1,x2,…,xn}が与えられると，次元 n が第1引数の座標チャートの名前から省略されることがある．
  • {coordsys,metric,dim}の形のトリプルの任意の，あるいはすべての要素を記号Allで置換することができる．この場合，CoordinateChartData[chart,property]は指定された要素にマッチする座標チャートのための値のリストを返す．
  • CoordinateChartData[]は，無限族の低次元メンバーのみを含む使用可能な座標チャートのリストを与える．
  • CoordinateChartData[chart]はCoordinateChartData[chart,"StandardName"]と等価である．
  • CoordinateChartData["Properties"]は使用可能な特性リストを返す．
  • 評価点{x1,x2,…,xn}が指定されていない場合，特性は一般に長さ n のリストが期待される純関数である．
  • 基本的な特性
  • "AlternateCoordinateNames"チャートに使われる，文字列としての一般的な代替座標名
    "CoordinateRangeAssumptions"チャートの座標によって満たされた仮説の論理式
    "Dimension"次元
    "ParameterRangeAssumptions"チャートのパラメータによって満たされた仮説の論理式
    "StandardCoordinateNames"チャートに使われる最も一般的な座標名の文字列としての名前
    "StandardName"Wolfram言語の標準名
  • 計量関連特性
  • "InverseMetric"座標基底の逆（反変）計量テンソルの成分
    "Metric"座標基底の計量テンソルの成分
    "ScaleFactors"リストとしての直交チャートのスケール因子
    "VolumeFactor"体積積分での微分係数
  • 整数 n のユークリッド座標チャート{coordsys,"Euclidean",n}の有効な coordsys 値には以下がある．
  • "Cartesian"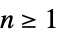についての直交座標
    "Hyperspherical"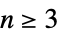について極が 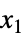軸に沿っている球座標と 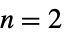についての極座標
    {"Confocal", {α1,…,αn}}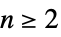について長半径 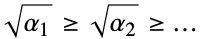である共焦点座標と下から昇順で有界の座標
  • 二次元のユークリッド座標チャート{coordsys,"Euclidean",2}の有効な coordsys 値には以下がある．
  • "Polar"極座標
    {"Bipolar",{a}}焦点距離が2a で，焦点角度，対数半径の順の二極座標
    {"Elliptic",{a}}焦点距離が2a で，双曲線半径，方位角の順の楕円座標
    "PlanarParabolic"二次元放物線座標
  • 三次元ユークリッド座標チャート{coordsys,"Euclidean",3}の有効な coordsys 値には以下がある．
  • "Cylindrical"極円柱座標
    "Spherical"極が 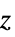軸に沿っていて，座標が半径，極角度，方位角の順の球座標
    {"BipolarCylindrical",{a}}焦点距離が 2a で焦点角度，対数半径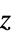， の順の二極円柱座標
    {"Bispherical",{a}}焦点距離が 2a で焦点角度，対数半径，方位角の順の両球座標
    "CircularParabolic"最終座標が方位角である放物線座標
    {"ConfocalParaboloidal", {α,β}} 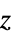軸を中心とし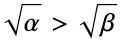， で座標が昇順で正の共焦点放物線座標
    {"Conical",{b,c}}パラメータ 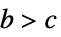の円錐座標
    {"EllipticCylindrical", {a}}焦点距離が 2a で双曲線半径，方位角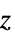， の順の楕円円柱座標
    {"OblateSpheroidal",{a}}焦点距離が 2a で双曲線半径，極角度，方位角の順の扁平楕円球座標
    "ParabolicCylindrical"放物線円柱座標
    {"ProlateSpheroidal",{a}}焦点距離が 2a で双曲線半径，極角度，方位角の順の長球座標
    {"Toroidal",a}環の半径が 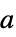で，対数半径，焦点角度，方位角の順のトロイダル座標
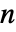  • 球面上の座標グラフ{coordsys,"Sphere",n}における，有効な coordsys の値
  • "Standard"標準角座標
    "Stereographic"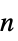
  • 球面への立体射影

例題

すべて開くすべて閉じる

例  (1)

三次元球座標：

スコープ  (22)

名前  (7)

CoordinateChartData[]は，無限族の低次元メンバーのみを含む使用可能なチャートのリストを与える：

ペア{coordsys,dim}は{coordsys,"Euclidean",dim}と等価である：

評価点が与えられている場合，第1引数から次元が省略されることがある：

ユークリッド計量のためのいくつかの特別な座標チャートは，座標系の名前だけを使って入力することができる：

既知の平面空間の三次元座標系すべてをリストする：

ペア{chart,dim}は{chart,"Euclidean",dim}と等価である：

使用可能な全二次元座標：

無限族の場合，低次元の代表が返される：

パラメータを指定すると関係のある次元が限られることがある：

マッチするチャートがない場合は，空リストが返される：

特性  (2)

使用可能な特性のリストを得る：

1つのチャートのスケール因子を与える：

平面空間のすべての二次元座標系を取り出す：

対応するスカラー因子を与える：

特性値  (2)

特性値には有効な任意のWolfram言語の式を使うことができる：

ほとんどの特性の場合，評価点が与えられないと，CoordinateChartDataは純関数を返す：

この関数は点に適用することができる：

明らかに変数に依存しないある種の記述特性は，特性値として純関数を返すことがない：

この現象が起る特性には"Dimension"，"ParameterRangeAssumptions"，"StandardName"，"StandardCoordinateNames"，"AlternateCoordinateNames"がある．

特性の詳細  (11)

基本的な特性  (7)

一般に，座標チャートは標準名で参照される：

これは，より単純なシンタックスと等価である：

チャート名でパターンマッチをせずに座標チャートの次元を検索する：

極座標の範囲の仮説を与える：

仮説はAssumptionsを取るSimplifyやその他の関数で使うことができる形で返される：

点を指定せずに"CoordinateRangeAssumptions"を使って点の有効性のための検定を作成する：

これは球座標の有効な点である：

これらは球座標の有効な点ではない：

同焦点楕円球座標のパラメータについての仮定を与える：

パラメータの特定の値が有効かどうかの検定を行う：

仮定に反するパラメータの値が使用されている場合は，メッセージが出され，CoordinateChartDataは未評価で返される：

球座標で使われる標準の座標名を検索する：

名前は文字列として与えられる：

ToExpressionを使ってこれらを記号に変換する：

球座標で使われる一般的な代替座標名を検索する：

名前は文字列である：

ToExpressionを使ってこれらを記号に変換する：

計量関連特性  (4)

（共変）計量の成分を行列として与える：

曲線に特化することで，計量を使って微分弧長を計算することができる：

逆（反変）計量の成分を行列をとして与える：

パラメータ a の特定の値の逆計量：

スケール因子を平坦なリストとして与える：

正規直交座標系では，スケール因子はスカラー勾配を偏微分に関連させる：

球座標で微分係数を与える：

領域のボリュームを求める：

ボリュームは 次元のボリュームである．例えば，二次元では面積に相当する：

アプリケーション  (1)

特定の座標系で曲線の微分弧長を計算する関数：

極座標での一般的な曲線の微分弧長：

円柱座標で表された螺線の微分弧長：

これを積分することができる：

特性と関係  (1)

CoordinateChartDataで，入力がチャートの座標範囲の仮定に従うことを確かめる：

2つの引数を持つ形式を使って一般式を抽出し，それを適用して単一点に拡張する：

インタラクティブな例題  (1)

二次元座標系のラプラス方程式のインタラクティブな表を作る：

Wolfram Research (2012), CoordinateChartData, Wolfram言語関数， https://reference.wolfram.com/language/ref/CoordinateChartData.html （2014年に更新）.

テキスト

Wolfram Research (2012), CoordinateChartData, Wolfram言語関数， https://reference.wolfram.com/language/ref/CoordinateChartData.html （2014年に更新）.

CMS

Wolfram Language. 2012. "CoordinateChartData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/CoordinateChartData.html.

APA

Wolfram Language. (2012). CoordinateChartData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoordinateChartData.html

BibTeX

@misc{reference.wolfram_2024_coordinatechartdata, author="Wolfram Research", title="{CoordinateChartData}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/CoordinateChartData.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_coordinatechartdata, organization={Wolfram Research}, title={CoordinateChartData}, year={2014}, url={https://reference.wolfram.com/language/ref/CoordinateChartData.html}, note=[Accessed: 25-November-2024 ]}