CoordinateChartData

CoordinateChartData[chart,property]

给出 chart 的指定属性值.

CoordinateChartData[chart,property,{x1,x2,…,xn}]

给出 chart 在点 {x1,x2,…,xn} 计算的指定属性值.

更多信息

  • 坐标图可以通过坐标系统名称、值对 {coordsys,dim} 或形如 {coordsys,metric,dim} 的标准名称给出. 维度 dim 是正整数. 值对 {coordsys,dim} 被解释为指欧几里得度量.
  • 有效的度量规范包括：
  • "metric"具有默认参数值的度量
    {"metric",param}指定单个参数的度量
    {"metric",{param1,param2,…}}指定多个参数的度量
  • 有效的坐标系统规范包括：
  • "coordsys"具有默认参数值的坐标系统
    {"coordsys",param}指定单个参数的坐标系统
    {"coordsys",{param1,param2,…}}指定多个参数的坐标系统
  • 如果给定了计算点 {x1,x2,…,xn}，维度 n 可以从第一个参数的坐标图名称中忽略.
  • 三元组 {coordsys,metric,dim} 中的任意或全部元素可以用符号 All 替换. 在这种情况下，CoordinateChartData[chart,property] 将返回坐标图的一个值列表，与指定元素匹配.
  • CoordinateChartData[] 给出一个可用坐标图的列表，仅包括低维有限族成员.
  • CoordinateChartData[chart] 等价于 CoordinateChartData[chart,"StandardName"].
  • CoordinateChartData["Properties"] 一个可用属性的列表.
  • 当没有给定计算点 {x1,x2,…,xn} 时，属性通常为纯函数， 期望一个长度为 n 的列表.
  • 基本属性包括：
  • "AlternateCoordinateNames"用于图表的常见备用坐标的名称，为字符串形式
    "CoordinateRangeAssumptions"坐标图所满足的假设的逻辑表达式
    "Dimension"维度
    "ParameterRangeAssumptions"图表参数所满足的假设的逻辑表达式
    "StandardCoordinateNames"用于图表的最常见坐标名称的名称，为字符串形式
    "StandardName"Wolfram 语言标准名称
  • 度量相关的属性包括：
  • "InverseMetric"坐标基上逆（逆变）度量张量的分量
    "Metric"坐标基上度量张量的分量
    "ScaleFactors"正交图表的尺寸缩放因子，为列表形式
    "VolumeFactor"体积积分的微分系数
  • 在欧几里得坐标图 {coordsys,"Euclidean",n} 中，对于整数 n，有效的 coordsys 值包括：
  • "Cartesian"笛卡尔坐标，其中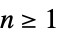
    "Hyperspherical"对于 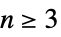，为极线沿 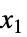轴的球面坐标，对于 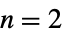，为极坐标
    {"Confocal", {α1,…,αn}}具有坐标下界的升序共焦坐标和半主轴 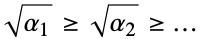，其中 .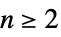
  • 在二维欧几里德坐标图 {coordsys,"Euclidean",2} 中，有效的 coordsys 值包括：
  • "Polar"极坐标
    {"Bipolar",{a}}焦距长度为 2a 的双极坐标，顺序为焦点角、对数半径
    {"Elliptic",{a}}焦距长度为 2a 的椭圆坐标，顺序为双曲半径、方位角
    "PlanarParabolic"二维抛物坐标
  • 在三维欧几里德坐标图 {coordsys,"Euclidean",3} 中，有效的 coordsys 值包括：
  • "Cylindrical"圆柱极坐标
    "Spherical"极线沿 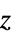轴的球面坐标和以半径、极角、方位角为序的坐标
    {"BipolarCylindrical",{a}}圆柱双极坐标，其中焦距长度为 2a，以焦点角、对数半径、 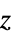为序
    {"Bispherical",{a}}双球面坐标，其中焦距长度为 2a，以焦点角、对数半径、方位角为序
    "CircularParabolic"抛物线坐标，其中最后一个坐标方位角
    {"ConfocalParaboloidal", {α,β}}在 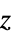轴上的共焦抛物面坐标，其中焦距 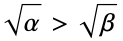，坐标为升序正坐标
    {"Conical",{b,c}}圆锥形坐标，其中参数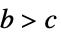
    {"EllipticCylindrical", {a}}椭圆圆柱坐标系，其中焦距长度为 2a，以双曲半径、方位角 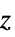为序
    {"OblateSpheroidal",{a}}扁圆椭球坐标，其中焦距长度为 2a，以双曲半径、极角、方位角为序
    "ParabolicCylindrical"抛物圆柱坐标
    {"ProlateSpheroidal",{a}}椭球坐标，其中焦距为 2a，以双曲半径、极角、方位角为序
    {"Toroidal",a}环形坐标，其中环半径为 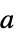，以半径、焦点角、方位角为序
  • 在 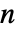-球上的坐标图{coordsys,"Sphere",n} 的有效 coordsys 值包括：
  • "Standard"标准角坐标
    "Stereographic"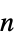
  • 平面上的球极平面投影

范例

打开所有单元关闭所有单元

基本范例  (1)

三维球面坐标：

范围  (22)

名称  (7)

CoordinateChartData[] 返回一个可用图表的列表，仅包括低维有限族的成员：

值对 {coordsys,dim} 等价于 {coordsys,"Euclidean",dim}：

当给定计算点时，维度可以从第一个参数中忽略：

欧几里德度量的一些特殊坐标图可以仅使用坐标系名称输入：

列出平面空间所有已知的三维坐标系：

值对 {chart,dim} 等价于 {chart,"Euclidean",dim}：

所有可用的二维坐标系：

对于有限族，返回低维的表示：

指定参数可能会限制相关的维度：

如果没有匹配的图表，则返回空列表：

属性  (2)

获取可能属性的列表：

给出单个图表的比例因子：

检索平面空间上的所有二维坐标系：

给出对应的比例因子：

属性值  (2)

属性值可以是任意有效的 Wolfram 语言表达式：

对于大多数属性，如果不给出计算点，CoordinateChartData 将返回一个纯函数：

此函数可以应用于点：

某些显然不依赖于变量的描述性属性，从不返回纯函数作为属性值：

发生这种情况的属性包括 "Dimension"、"ParameterRangeAssumptions"、"StandardName"、"StandardCoordinateNames" 和 "AlternateCoordinateNames".

详细属性  (11)

基本属性  (7)

一般情况下，坐标图用标准名称引用：

这等价于这个较简单的语法：

查看坐标图维度，而不对图表名称进行模式匹配：

给出极坐标范围的假设：

假设返回的形式可用于 Simplify 及其他接受 Assumptions 的函数：

使用 "CoordinateRangeAssumptions"，不指定点来创建一个点的有效性测试：

在球坐标系中，这是一个有效的点：

这些都不是球面坐标的有效点：

给出椭球坐标系中的参数假设：

测试一个特定参数值是否有效：

如果参数值与所用假设冲突，将生成一条消息，CoordinateChartData 以未计算的形式返回：

查找用于球面坐标的标准坐标名称：

名称以字符串的形式给出：

使用 ToExpression 将它们转换为符号：

查找用于球面坐标的其他常用坐标名称：

名称为字符串：

使用 ToExpression 将它们转换为符号：

与度量相关的属性  (4)

给出矩阵形式的（协变）度量分量：

通过特殊化曲线，度量可用于计算差分弧长：

给出矩阵形式的逆（逆变）度量分量：

具有特定参数值 a 的逆度量：

以展平列表的形式给出比例因子：

在正交坐标系中，比例因子将标量梯度与偏微分相关联：

给出球面坐标的微分系数：

求一个区域的体积：

体积是一个 -维体积. 比如，在二维情况下对应于面积：

应用  (1)

在特定坐标系统中计算曲线微分弧长的函数：

极坐标系中一般曲线的微分弧长：

在圆柱坐标系中表示的螺旋线的微分弧长：

现在可以进行积分：

属性和关系  (1)

CoordinateChartData 检查输入服从图表坐标范围的假设：

提取使用两个参数形式的一般公式，并运用它来扩展到奇点：

互动范例  (1)

在二维坐标系中创建一个拉普拉斯表达式的交互式表格：

Wolfram Research (2012)，CoordinateChartData，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CoordinateChartData.html （更新于 2014 年）.

文本

Wolfram Research (2012)，CoordinateChartData，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CoordinateChartData.html （更新于 2014 年）.

CMS

Wolfram 语言. 2012. "CoordinateChartData." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/CoordinateChartData.html.

APA

Wolfram 语言. (2012). CoordinateChartData. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CoordinateChartData.html 年

BibTeX

@misc{reference.wolfram_2024_coordinatechartdata, author="Wolfram Research", title="{CoordinateChartData}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/CoordinateChartData.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_coordinatechartdata, organization={Wolfram Research}, title={CoordinateChartData}, year={2014}, url={https://reference.wolfram.com/language/ref/CoordinateChartData.html}, note=[Accessed: 25-November-2024 ]}