CoreNilpotentDecomposition
正方行列 m のコアベキ零分解を与える.
CoreNilpotentDecomposition[m,format]
指定の format に従ってコアベキ零分解を返す.
詳細とオプション

- CoreNilpotentDecomposition[m]は行列のリスト{t,c,n}を返す.ただし,コア行列 c は非特異行列で行列 n はベキ零行列である. »
- 行列 m はそのコアベキ零分解と
![m=t.(c 0; 0 n).TemplateBox[{t}, Inverse] m=t.(c 0; 0 n).TemplateBox[{t}, Inverse]](Files/CoreNilpotentDecomposition.ja/1.png) によって関係している.
によって関係している. - ベキ零行列 n について,MatrixPower[n,p]が零行列となるような非負の整数
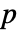 (行列 m の指標)が存在する.
(行列 m の指標)が存在する. - 行列のコアベキ零分解を使って,定数係数を持つ線形微分代数(あるいは差分代数)方程式の系を解くことができる.
- コア部分またはベキ零部分が自明のときは,自明の部分に対して空リスト{}が返される. »
- CoreNilpotentDecomposition[m]はCoreNilpotentDecomposition[m,"SplitBlocks"]に等しい.
- CoreNilpotentDecomposition[m,"BlockDiagonal"]は行列{t,d}のリストを返す.ただし,
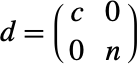 である.
である. - TargetStructure->"Dense"の設定のとき,CoreNilpotentDecomposition[m,"BlockDiagonal"]は行列のリスト{t,d}を返す.ただし,
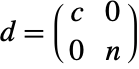 である.
である. - TargetStructure->"Structured"の設定のとき,リスト{t,d}の行列
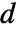 はBlockDiagonalMatrixとして表される.
はBlockDiagonalMatrixとして表される.
例題
すべて開くすべて閉じるスコープ (12)
基本的な用法 (7)
CoreNilpotentDecomposition[m]はCoreNilpotentDecomposition[m,"SplitBlocks"]に等しい.ただし,コア部分とベキ零部分は分離されている:
CoreNilpotentDecomposition[m,"BlockDiagonal"]は,ブロック対角行列中にコア部分とベキ零部分をまとめる:
オプション (1)
TargetStructure (1)
TargetStructure->"Dense"のとき,CoreNilpotentDecomposition[m,"BlockDiagonal"]は2つの行列のリストを返す:
2番目の行列は,コア部分とベキ零部分からなるブロック対角行列である:
TargetStructure->"Structured"のとき,2番目の行列はBlockDiagonalMatrixとして表される:
アプリケーション (2)
![]() と
と ![]() はどちらも特異なので,この方程式は標準形
はどちらも特異なので,この方程式は標準形 ![]() にすることはできない:
にすることはできない:
DSolveValueの結果と比較する:
特性と関係 (4)
CoreNilpotentDecompositionはトリプル{t,c,n}を返す:
もとの行列 m はそのコアベキ零分解によって表すことができる:
それにもかかわらず,BlockDiagonalMatrixを使って表された恒等式は成立する:
それにもかかわらず,BlockDiagonalMatrixを使って表された恒等式は成立する:
考えられる問題 (2)
BlockDiagonalMatrixは{}を0×0行列と解釈するので,この関数を使ってもとの行列を再構築する:
テキスト
Wolfram Research (2021), CoreNilpotentDecomposition, Wolfram言語関数, https://reference.wolfram.com/language/ref/CoreNilpotentDecomposition.html (2023年に更新).
CMS
Wolfram Language. 2021. "CoreNilpotentDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/CoreNilpotentDecomposition.html.
APA
Wolfram Language. (2021). CoreNilpotentDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoreNilpotentDecomposition.html