WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

RSolve
✖
RSolve

Updatedshow changeshide changes

✖
RSolve[eqn,a[n],n]

solves a recurrence equation for a[n].

✖
RSolve[{eqn1,eqn2,…},{a1[n],a2[n],…},n]

solves a system of recurrence equations.

✖
RSolve[eqn,a[n1,n2,…],{n1,n2,…}]

solves a partial recurrence equation.

Details and Options

  • RSolve[eqn,a,n] gives solutions for a as pure functions.
  • The equations can involve objects of the form a[n+λ] where λ is a constant, or in general, objects of the form a[ψ[n]], a[ψ[ψ[n]], a[ψ[…[ψ[n]]…]], where ψ can have forms such as:
  • n+λarithmetic difference equation
    μ ngeometric or 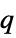-difference equation
    μ n+λarithmetic-geometric functional difference equation
    μ nαgeometric-power functional difference equation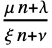
    linear fractional functional difference equation
  • Equations such as a[0]==val can be given to specify end conditions.
  • If not enough end conditions are specified, RSolve will give general solutions in which undetermined constants are introduced.
  • The specification a∈Vectors[m] or a∈Matrices[{m,p}] can be used to indicate that the dependent variable a is a vector-valued or a matrix-valued variable, respectively. Alternatively, a can be specified as a VectorSymbol or MatrixSymbol. » »
  • The constants introduced by RSolve are indexed by successive integers. The option GeneratedParameters specifies the function to apply to each index. The default is GeneratedParameters->C, which yields constants C[1], C[2], ….
  • GeneratedParameters->(Module[{C},C]&) guarantees that the constants of integration are unique, even across different invocations of RSolve.
  • For partial recurrence equations, RSolve generates arbitrary functions C[n][…].
  • Solutions given by RSolve sometimes include sums that cannot be carried out explicitly by Sum. Dummy variables with local names are used in such sums.
  • RSolve sometimes gives implicit solutions in terms of Solve.
  • RSolve handles both ordinary difference equations and 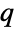‐difference equations.
  • RSolve handles difference‐algebraic equations as well as ordinary difference equations.
  • RSolve can solve linear recurrence equations of any order with constant coefficients. It can also solve many linear equations up to second order with nonconstant coefficients, as well as many nonlinear equations.

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Solve a difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-beykdi
Out[1]=1

Include a boundary condition:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-fcprab
Out[1]=1

Get a "pure function" solution for a:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-lkwyp
Out[1]=1

Substitute the solution into an expression:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-blbvxk
Out[2]=2

Solve a functional equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-lb5zc
Out[1]=1

Scope  (40)Survey of the scope of standard use cases

Basic Uses  (7)

Compute the general solution of a first-order difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-gavkfv
Out[1]=1

Obtain a particular solution by adding an initial condition:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-cpyb5j
Out[2]=2

Plot the solution of a first-order difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-dq38m6
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-gwsnkl
Out[2]=2

Make a table of values:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-g7e9fj
Out[3]=3

Verify the solution of a difference equation by using a in the second argument:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-m3ku4s
In[2]:=2
✖
https://wolfram.com/xid/0giurm-dx4u90
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-hvjrw
Out[3]=3

Obtain the general solution of a higher-order difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-h41qz6
Out[1]=1

Particular solution:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-e03uxz
Out[2]=2

Solve a system of difference equations:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-cn9tge
In[2]:=2
✖
https://wolfram.com/xid/0giurm-gywblx
Out[2]=2

Plot their solution:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-doi666
Out[3]=3

Verify the solution:

In[4]:=4
✖
https://wolfram.com/xid/0giurm-bz9hgr
Out[4]=4

Solve a partial difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-ceeu8p
Out[1]=1

Obtain a particular solution:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-dype01
Out[2]=2

Plot the resulting solution:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-e3xd9u
Out[3]=3

Use different names for the arbitrary constants in the general solution:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-gmwx2k
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-crng6n
Out[2]=2

Linear Difference Equations  (7)

Geometric equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-b3rl6x
Out[1]=1

First-order equation with variable coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-df4eb2
Out[1]=1

A third-order constant coefficient equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-d2ylip
Out[1]=1

Initial value conditions:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-ud55e
Out[2]=2

Plot the solution:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-bimqsv
Out[3]=3

Second-order inhomogeneous equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-b2w51x
Out[1]=1

Second-order variable coefficient equation in terms of elementary functions:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-6bgvt
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-9h713
Out[2]=2

Euler–Cauchy equation:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-cxvz9
Out[3]=3

In general, special functions are required to express solutions:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-gb5jys
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-fca2vd
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-bbtdnv
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0giurm-enl0nf
Out[4]=4

Higher-order inhomogeneous equation with constant coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-b8dnre
Out[1]=1

Nonlinear Difference Equations  (5)

Solvable logistic equations:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-jswrw
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-fme213
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-dzjux3
Out[3]=3

Riccati equations:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-bely1i
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-b5ly0z
Out[2]=2

Solutions in terms of trigonometric and hyperbolic functions:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-fg44ia
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-d1mu12
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-bbram
Out[3]=3

Higher-order equations:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-bzvq2g
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-brp7m
Out[2]=2

Nonlinear convolution equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-c9211f
Out[1]=1

Systems of Difference Equations  (8)

Linear system with constant coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-lcnds
Out[1]=1

With boundary conditions:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-e1ny7c
Out[2]=2

Plot their solution:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-bbj3i4
Out[3]=3

Linear fractional systems:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-grumcj
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-e9dec0
Out[2]=2

Diagonal system:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-d8vn48
Out[1]=1

Variable coefficient linear system with a polynomial solution:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-paipl
Out[1]=1

Linear constant coefficient difference-algebraic system:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-b8wcbi
Out[1]=1

An index-2 system:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-f6qeoo
Out[2]=2

Solve a linear system using vector variables:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-bo599y
In[2]:=2
✖
https://wolfram.com/xid/0giurm-bzpwfn
Out[2]=2

Alternatively, define as a VectorSymbol:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-cv8zz4
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0giurm-fmn0k1
Out[4]=4

Solve a linear system using matrix variables:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-2cuti
In[2]:=2
✖
https://wolfram.com/xid/0giurm-dl2agr

Alternatively, define as a MatrixSymbol:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-b0s71
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0giurm-guj4cm

Solve an inhomogeneous linear system of ODEs with constant coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-bp8x41
In[2]:=2
✖
https://wolfram.com/xid/0giurm-dcp6p7
Out[2]=2

Partial Difference Equations  (3)

First-order linear partial difference equation with constant coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-grk4h7
Out[1]=1

Substitute the function Sin[2k] for the free function C[1]:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-bvnuue
Out[2]=2

Plot the resulting solution:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-dwt1s6
Out[3]=3

Constant coefficient linear equation of orders 2, 3, and 4:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-753en
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-ght6pb
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-kpwi66
Out[3]=3

Inhomogeneous:

In[4]:=4
✖
https://wolfram.com/xid/0giurm-n1pkey
Out[4]=4

Variable coefficient linear equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-mm44i
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-4hvtt
Out[2]=2

Q–Difference Equations  (6)

First-order constant coefficient -difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-nlpjs
Out[1]=1

Equivalent way of expressing the same equation:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-cvpmf0
Out[2]=2

Initial value:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-bmm4gv
Out[3]=3

Second-order equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-dy27zf
Out[1]=1

Third-order:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-e8m5yy
Out[2]=2

Inhomogeneous:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-bcwf4t
Out[3]=3

Using a numeric value for :

In[1]:=1
✖
https://wolfram.com/xid/0giurm-hbwbk
Out[1]=1

Plot solution:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-bta89c
Out[2]=2

Linear varying coefficient equations:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-ekqufq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-b8s46
Out[2]=2

Nonlinear equations:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-1tc12
Out[1]=1

Riccati equation:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-gh3pk2
Out[2]=2

A linear constant coefficient system of -difference equations:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-bjdev
Out[1]=1

Functional Difference Equations  (4)

Find the general solution for an arithmetic difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-eskt6u
Out[1]=1

Verify the solution:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-fl8wyk
Out[2]=2

Solve an initial value problem for an arithmetic-geometric difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-lq8uxp
Out[1]=1

Plot the solution:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-cp1baa
Out[2]=2

Solve a linear fractional difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-et0rui
Out[1]=1

Make a table of values for the solution:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-opvo0
Out[2]=2

Solve a geometric power difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-cyt0mg
Out[1]=1

Verify the solution:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-xoj7g
Out[2]=2

Generalizations & Extensions  (1)Generalized and extended use cases

No boundary condition, gives two generated parameters:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-l7we97
Out[1]=1

One boundary condition:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-i2noix
Out[2]=2

Two boundary conditions:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-dy7e1x
Out[3]=3

Options  (1)Common values & functionality for each option

GeneratedParameters  (1)

Use differently named constants:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-c14jm7
Out[1]=1

Use subscripted constants:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-f5orp6
Out[2]=2

Applications  (11)Sample problems that can be solved with this function

This models the amount a[n] at year n when the interest r is paid on the principal p only:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-ivnehp
Out[1]=1

Here the interest is paid on the current amount a[n], i.e. compound interest:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-grc5tc
Out[2]=2

Here a[n] denotes the number of moves required in the Tower of Hanoi problem with n disks:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-dirjin
Out[1]=1

Here a[n] is the number of ways to tile an n×3 space with 2×1 tiles:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-cgwxlr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-cvmhr5
Out[2]=2

The number of comparisons for a binary search problem:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-e12z9x
Out[1]=1

Number of arithmetic operations in the fast Fourier transform:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-ca0dv6
Out[2]=2

The integral satisfies the difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-b1zq6m
Out[1]=1

The integral satisfies the difference equation:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-bd29zb
Out[2]=2

The difference equation for the series coefficients of :

In[1]:=1
✖
https://wolfram.com/xid/0giurm-km6kay
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-bk3t21
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-bqldrr
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0giurm-etpos
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0giurm-i5reh6
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0giurm-9k53o
Out[6]=6

The determinant of an n×n tridiagonal matrix with diagonals satisfies:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-hkvmxc
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-fdr177
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-cd08vo
Out[3]=3

This models the surface area s[n] in dimension n of a unit sphere:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-dzn0wo
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-i1g568
Out[2]=2

The volume of the unit ball in dimension n:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-dg8ldc
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0giurm-b950i1
Out[4]=4

Applying Newton's method to , or computing :

In[1]:=1
✖
https://wolfram.com/xid/0giurm-c9y8fu
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-epqe6y
Out[2]=2

Applying the Euler forward method to yields:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-nv94x
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-yx75y
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-moj0r
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0giurm-hqi05m
Out[4]=4

Solve the difference equation that describes the complexity of Karatsuba multiplication:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-b37tk4
Out[1]=1

Compare with the complexity of schoolbook multiplication:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-i7ko1
Out[2]=2

Properties & Relations  (9)Properties of the function, and connections to other functions

Solutions satisfy their difference and boundary equations:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-kejbs5
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-g2pmc9
Out[2]=2

Difference equation corresponding to Sum:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-cl7803
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-va9gp
Out[2]=2

Difference equation corresponding to Product:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-b3ktdq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-ed0bzh
Out[2]=2

RSolve returns a rule for the solution:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-bpoct1
Out[1]=1

RSolveValue returns an expression for the solution:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-lhyf6h
Out[2]=2

RSolve finds a symbolic solution for a difference equation:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-uk6jh
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-4gnjt
Out[2]=2

RecurrenceTable generates a procedural solution for the same problem:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-dczj4k
Out[3]=3

FindLinearRecurrence finds the minimal linear recurrence for a list:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-ci0we0
Out[1]=1

RSolve finds the sequence satisfying the recurrence:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-fucxa1
Out[2]=2

Use RecurrenceFilter to filter a signal:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-bokwyk
Out[1]=1

Solve the corresponding difference equation using RSolve:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-jeb1nc
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-mb5dvy
Out[3]=3

Forecast the next value for a time series based on ARProcess:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-cvyshc
In[2]:=2
✖
https://wolfram.com/xid/0giurm-hwnsts
Out[2]=2

Obtain the same result using RSolve:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-i6a71
In[4]:=4
✖
https://wolfram.com/xid/0giurm-beqdzh
Out[4]=4

Use RFixedPoints to find the fixed points for a system of two recurrence equations:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-dfvuec
Out[1]=1

Use RStabilityConditions to analyze the stability of the fixed point:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-e1pdjo
Out[2]=2

Solve the system using a fixed point as the initial condition:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-bqt3d2
Out[3]=3

Solve the system for given initial conditions:

In[4]:=4
✖
https://wolfram.com/xid/0giurm-ew3s3y
Out[4]=4

Plot the solution:

In[5]:=5
✖
https://wolfram.com/xid/0giurm-cdxzlx
Out[5]=5

Possible Issues  (5)Common pitfalls and unexpected behavior

Results may contain symbolic sums and products:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-soveq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-d0ak58
Out[2]=2

Capital and capital cannot be used as independent variables:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-naf6p
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-jsf2d
Out[2]=2

Replacing them by lowercase or lowercase fixes the issue:

In[3]:=3
✖
https://wolfram.com/xid/0giurm-cey7sg
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0giurm-b5ffk1
Out[4]=4

The solution to this difference equation is unique as a sequence:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-i8mq3w
Out[1]=1

As a function it is only unique up to a function of period 1:

In[2]:=2
✖
https://wolfram.com/xid/0giurm-sne2w
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-cx5wn1
Out[3]=3

Boundary value problems may have multiple solutions:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-2z3dz
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-fqaozc
Out[2]=2

Verify the solution when the equation involves subscripted variables:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-hva8j2
In[2]:=2
✖
https://wolfram.com/xid/0giurm-fmeyte
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-gihqcn
Out[3]=3

Neat Examples  (1)Surprising or curious use cases

Compute the n^(th) iterate or composition of a function:

In[1]:=1
✖
https://wolfram.com/xid/0giurm-b8skxu
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0giurm-by1wy1
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0giurm-cdrelf
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0giurm-ft8w6
Out[4]=4
Wolfram Research (2003), RSolve, Wolfram Language function, https://reference.wolfram.com/language/ref/RSolve.html (updated 2025).
✖
Wolfram Research (2003), RSolve, Wolfram Language function, https://reference.wolfram.com/language/ref/RSolve.html (updated 2025).

Text

Wolfram Research (2003), RSolve, Wolfram Language function, https://reference.wolfram.com/language/ref/RSolve.html (updated 2025).

✖
Wolfram Research (2003), RSolve, Wolfram Language function, https://reference.wolfram.com/language/ref/RSolve.html (updated 2025).

CMS

Wolfram Language. 2003. "RSolve." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/RSolve.html.

✖
Wolfram Language. 2003. "RSolve." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/RSolve.html.

APA

Wolfram Language. (2003). RSolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RSolve.html

✖
Wolfram Language. (2003). RSolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RSolve.html

BibTeX

@misc{reference.wolfram_2025_rsolve, author="Wolfram Research", title="{RSolve}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/RSolve.html}", note=[Accessed: 28-April-2025 ]}

✖
@misc{reference.wolfram_2025_rsolve, author="Wolfram Research", title="{RSolve}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/RSolve.html}", note=[Accessed: 28-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_rsolve, organization={Wolfram Research}, title={RSolve}, year={2025}, url={https://reference.wolfram.com/language/ref/RSolve.html}, note=[Accessed: 28-April-2025 ]}

✖
@online{reference.wolfram_2025_rsolve, organization={Wolfram Research}, title={RSolve}, year={2025}, url={https://reference.wolfram.com/language/ref/RSolve.html}, note=[Accessed: 28-April-2025 ]}