CoreNilpotentDecomposition
生成方阵 m 的核-幂零分解.
CoreNilpotentDecomposition[m,format]
根据指定 format 返回核心-零分解.
更多信息和选项

- CoreNilpotentDecomposition[m] 返回矩阵列表 {t,c,n},其中核心矩阵 c 是非奇异矩阵,矩阵 n 是幂零矩阵. »
- 矩阵 m 与其核-幂零分解的关系是
![m=t.(c 0; 0 n).TemplateBox[{t}, Inverse] m=t.(c 0; 0 n).TemplateBox[{t}, Inverse]](Files/CoreNilpotentDecomposition.zh/1.png) .
. - 对于幂零矩阵 n,存在一个非负整数
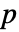 (矩阵 m 的索引) 使得 MatrixPower[n,p] 为零矩阵.
(矩阵 m 的索引) 使得 MatrixPower[n,p] 为零矩阵. - 矩阵的核-幂零分解可用于求解具有常系数的线性微分代数(或差分代数)方程组.
- 如果核心或幂零部分可忽略不计,则为该忽略不计的部分返回一个空列表 {}. »
- CoreNilpotentDecomposition[m] 等价于 CoreNilpotentDecomposition[m,"SplitBlocks"].
- CoreNilpotentDecomposition[m,"BlockDiagonal"] 返回矩阵列表 {t,d} 其中
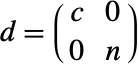 .
. - 设置 TargetStructure->"Dense",则 CoreNilpotentDecomposition[m,"BlockDiagonal"] 返回矩阵列表 {t,d} 其中
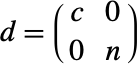 .
. - 设置 TargetStructure->"Structured",列表 {t,d} 中的矩阵
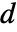 以 BlockDiagonalMatrix 的形式表示.
以 BlockDiagonalMatrix 的形式表示.
范例
打开所有单元关闭所有单元范围 (12)
基本用法 (7)
CoreNilpotentDecomposition[m] 等价于 CoreNilpotentDecomposition[m,"SplitBlocks"],其中核心部分和幂零部分保持分开:
CoreNilpotentDecomposition[m,"BlockDiagonal"] 将核心部分和幂零部分合并为一个块对角矩阵:
选项 (1)
TargetStructure (1)
设置 TargetStructure->"Dense",CoreNilpotentDecomposition[m,"BlockDiagonal"] 返回两个矩阵的列表:
设置 TargetStructure->"Structured",第二个矩阵会以 BlockDiagonalMatrix 的形式表示:
应用 (2)
对比 DSolveValue 给出的结果:
属性和关系 (4)
CoreNilpotentDecomposition 返回三元组 {t,c,n}:
尽管如此,使用 BlockDiagonalMatrix 表示的恒等式仍然成立:
尽管如此,使用 BlockDiagonalMatrix 表达的恒等式仍然成立:
可用 CoreNilpotentDecomposition 进行计算 DrazinInverse:
可能存在的问题 (2)
用 BlockDiagonalMatrix 重新构建原始矩阵,因为它将 {} 解释为 0×0 的矩阵:
文本
Wolfram Research (2021),CoreNilpotentDecomposition,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CoreNilpotentDecomposition.html (更新于 2023 年).
CMS
Wolfram 语言. 2021. "CoreNilpotentDecomposition." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/CoreNilpotentDecomposition.html.
APA
Wolfram 语言. (2021). CoreNilpotentDecomposition. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CoreNilpotentDecomposition.html 年