CorrelationFunction[data,hspec]
estimates the correlation function at lags hspec from data.
CorrelationFunction[proc,hspec]
represents the correlation function at lags hspec for the random process proc.
CorrelationFunction[proc,s,t]
represents the correlation function at times s and t for the random process proc.


CorrelationFunction
CorrelationFunction[data,hspec]
estimates the correlation function at lags hspec from data.
CorrelationFunction[proc,hspec]
represents the correlation function at lags hspec for the random process proc.
CorrelationFunction[proc,s,t]
represents the correlation function at times s and t for the random process proc.
Details

- CorrelationFunction is also known as autocorrelation or cross-correlation function (ACF or CCF).
- The following specifications can be given for hspec:
-
τ at time or lag τ {τmax} unit spaced from 0 to τmax {τmin,τmax} unit spaced from τmin to τmax {τmin,τmax,dτ} from τmin to τmax in steps of dτ {{τ1,τ2,…}} use explicit {τ1,τ2,…} - CorrelationFunction[{x1,…,xn},h] is equivalent to
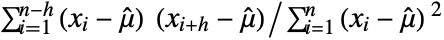 with
with 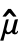 =Mean[{x1,…,xn}].
=Mean[{x1,…,xn}]. - When data is TemporalData containing an ensemble of paths, the output represents the average across all paths.
- CorrelationFunction of the process proc is the CovarianceFunction c normalized by the outer product of the standard deviation function σ at times s and t:
-
c[s,t]/(σ[s]σ[t]) for scalar-valued data or processes c[s,t]/(σ[s] ⊗ σ[t]) for vector-valued data or processes - The symbol ⊗ represents KroneckerProduct.
- CorrelationFunction[proc,h] is defined only if proc is a weakly stationary process and is equivalent to CorrelationFunction[proc,h,0].
- The process proc can be any random process, such as ARMAProcess and WienerProcess.
Examples
open all close allBasic Examples (4)
Scope (13)
Empirical Estimates (7)
Estimate the correlation function for some data at lag 9:
Obtain empirical estimates of the correlation function up to lag 9:
Compute the correlation function for lags 1 to 9 in steps of 2:
Compute the correlation function for a time series:
The correlation function of a time series for multiple lags is given as a time series:
Estimate the correlation function for an ensemble of paths:
Random Processes (6)
The correlation function for a weakly stationary discrete-time process:
The correlation function only depends on the antidiagonal ![]() :
:
The correlation function for a weakly stationary continuous-time process:
The correlation function only depends on the antidiagonal ![]() :
:
The correlation function for a non-weakly stationary discrete-time process:
The correlation function depends on both time arguments:
The correlation function for a non-weakly stationary continuous-time process:
The correlation function depends on both time arguments:
The correlation function for some time series processes:
Cross-correlation plots for a vector ARProcess:
Applications (2)
Determine whether the following data is best modeled with an MAProcess or an ARProcess:
It is difficult to determine the underlying process from sample paths:
The correlation function of the data decays slowly:
ARProcess is clearly a better candidate model than MAProcess:
Create an ACF plot with white-noise confidence bands:
Plot the correlation for lags 0 to 20 with 95% white-noise confidence bands:
Properties & Relations (12)
Sample correlation function is a biased estimator for the process correlation function:
Calculate the sample correlation function:
Correlation function for the process:
Correlation function for a process is the off-diagonal entry in the Correlation matrix:
Sample correlation at lag 0 is always 1:
Sample correlation function is related to CovarianceFunction:
Scaled sample covariance function:
Sample correlation function is related to AbsoluteCorrelationFunction:
Compare to the sample correlation function:
Use Expectation to calculate correlation:
Define mean and standard deviation functions:
Correlation function for equal times reduces to 1:
Correlation function ![]() is related to the CovarianceFunction
is related to the CovarianceFunction ![]() :
:
For ![]() , the standard deviation function is
, the standard deviation function is ![]() :
:
The correlation function is related to the Correlation:
It is the off-diagonal entry in the covariance matrix:
Correlation function is invariant for ToInvertibleTimeSeries:
Correlation function is invariant to centralizing:
Compare correlation functions:
Sum of the sample correlation function is constant:
Possible Issues (1)
CorrelationFunction output may contain DifferenceRoot:
Use FunctionExpand to recover explicit powers:
Related Guides
History
Text
Wolfram Research (2012), CorrelationFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/CorrelationFunction.html.
CMS
Wolfram Language. 2012. "CorrelationFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CorrelationFunction.html.
APA
Wolfram Language. (2012). CorrelationFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CorrelationFunction.html
BibTeX
@misc{reference.wolfram_2025_correlationfunction, author="Wolfram Research", title="{CorrelationFunction}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CorrelationFunction.html}", note=[Accessed: 13-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_correlationfunction, organization={Wolfram Research}, title={CorrelationFunction}, year={2012}, url={https://reference.wolfram.com/language/ref/CorrelationFunction.html}, note=[Accessed: 13-January-2026]}